【题目描述】
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中,牌的大小关系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
具体规则如下:
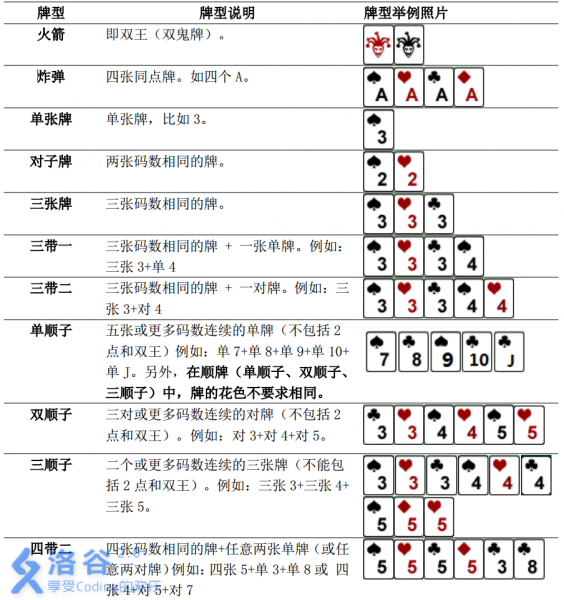
本题数据随机,不支持hack,要hack或强力数据请点击这里
输入输出格式
输入格式:
第一行包含用空格隔开的2个正整数T和n,表示手牌的组数以及每组手牌的张数。
接下来T组数据,每组数据n行,每行一个非负整数对aibi表示一张牌,其中ai示牌的数码,bi表示牌的花色,中间用空格隔开。特别的,我们用1来表示数码A,11表示数码J,12表示数码Q,13表示数码K;黑桃、红心、梅花、方片分别用1-4来表示;小王的表示方法为01,大王的表示方法为02。
输出格式:
共T行,每行一个整数,表示打光第i手牌的最少次数。
输入输出样例
1 8 7 4 8 4 9 1 10 4 11 1 5 1 1 4 1 1
3
1 17 12 3 4 3 2 3 5 4 10 2 3 3 12 2 0 1 1 3 10 1 6 2 12 1 11 3 5 2 12 4 2 2 7 2
6
说明
样例1说明
共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
对于不同的测试点, 我们约定手牌组数T与张数n的规模如下:
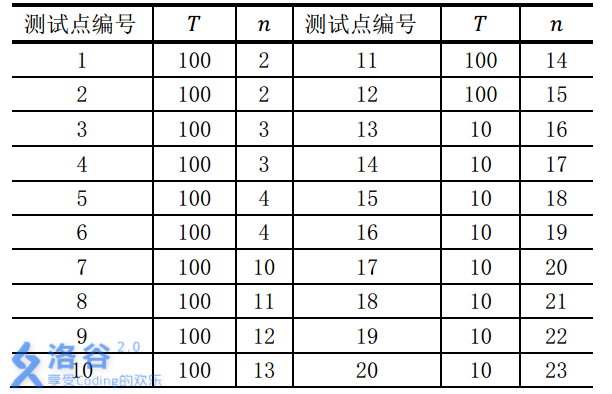
数据保证:所有的手牌都是随机生成的。
自测时果断打了个状压dp,其中f[i]表示当前手上牌的状态为i时需要的最少出牌次数(i的第k个二进制位表示排序后的第k张牌是否出手)。f[i]的转移比较复杂,因此代码打了200+行.....
时间复杂度为O(4*3^7),但由于f[i]转移条件判断较为耗时,转移方法较多,常数巨大!!
结果这个状压代码只拿了80分...最后四个点TLE(如果不是多组数据就A了.....)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define M 18 6 #define N 14 7 #define INF 123123123 8 using namespace std; 9 int n,st,f[1<<24]={0},cnt[M]={0},a[M]={0},l[M]={0},r[M]={0}; 10 11 bool hf(int x){ 12 bool wei1,wei2; 13 for(int i=1;i<n;i++){ 14 wei1=x&(1<<i); wei2=x&(1<<(i-1)); 15 if(a[i]==a[i-1]&&wei2&&(!wei1)) return 0; 16 } 17 return 1; 18 } 19 int dan(int y,int x){ 20 if(l[x]==-1) return st; 21 int k=(1<<(r[x]-l[x]+1))-1; 22 int delta=(y>>l[x])&k; 23 if(delta){ 24 delta=(delta<<1)&k; 25 y=(y&((1<<l[x])-1))|(delta<<l[x])|((y>>(r[x]+1))<<(r[x]+1)); 26 return y; 27 } 28 return st; 29 } 30 int dui(int y,int x){ 31 if(l[x]==-1) return st; 32 int k=(1<<(r[x]-l[x]+1))-1; 33 int delta=(y>>l[x])&k; 34 if((delta<<1)&k){ 35 delta=(delta<<2)&k; 36 y=(y&((1<<l[x])-1))|(delta<<l[x])|((y>>(r[x]+1))<<(r[x]+1)); 37 return y; 38 } 39 return st; 40 } 41 int san(int y,int x){ 42 if(l[x]==-1) return st; 43 int k=(1<<(r[x]-l[x]+1))-1; 44 int delta=(y>>l[x])&k; 45 if((delta<<2)&k){ 46 delta=(delta<<3)&k; 47 y=(y&((1<<l[x])-1))|(delta<<l[x])|((y>>(r[x]+1))<<(r[x]+1)); 48 return y; 49 } 50 return st; 51 } 52 int zha(int y,int x){ 53 if(l[x]==-1) return st; 54 int k=(1<<(r[x]-l[x]+1))-1; 55 int delta=(y>>l[x])&k; 56 if((delta<<3)&k){ 57 delta=(delta<<4)&k; 58 y=(y&((1<<l[x])-1))|(delta<<l[x])|((y>>(r[x]+1))<<(r[x]+1)); 59 return y; 60 } 61 return st; 62 } 63 int sandaiyi(int y,int x,int dai){ 64 y=san(y,x); 65 if(y==st) return st; 66 return dan(y,dai); 67 } 68 int sandaier(int y,int x,int dai){ 69 y=san(y,x); 70 if(y==st) return st; 71 return dui(y,dai); 72 } 73 int sidaier(int y,int x,int dai1,int dai2){ 74 y=zha(y,x); 75 if(y==st) return st; 76 y=dan(y,dai1); 77 if(y==st) return st; 78 return dan(y,dai2); 79 } 80 int sidaidui(int y,int x,int dai1,int dai2){ 81 y=zha(y,x); 82 if(y==st) return st; 83 y=dui(y,dai1); 84 if(y==st) return st; 85 return dui(y,dai2); 86 } 87 int shunzi(int y,int ll,int rr){ 88 for(int i=ll;i<=rr;i++){ 89 y=dan(y,i); 90 if(y==st) return st; 91 } 92 return y; 93 } 94 int liandui(int y,int ll,int rr){ 95 for(int i=ll;i<=rr;i++){ 96 y=dui(y,i); 97 if(y==st) return st; 98 } 99 return y; 100 } 101 int sanshun(int y,int ll,int rr){ 102 for(int i=ll;i<=rr;i++){ 103 y=san(y,i); 104 if(y==st) return st; 105 } 106 return y; 107 } 108 int Main(){ 109 memset(cnt,0,sizeof(cnt)); 110 memset(a,0,sizeof(a)); 111 memset(l,-1,sizeof(l)); memset(r,-1,sizeof(r)); 112 for(int i=1;i<=n;i++){ 113 int x,k; scanf("%d%d",&x,&k); 114 if(x<3){ 115 if(x==0) x=2; 116 else if(x==2) x=1; 117 else x=0; 118 } 119 x=1+(x-3+N)%N; 120 cnt[x]++; 121 } 122 for(int i=1,j=0;i<=N;i++){ 123 bool ck=1; 124 while(cnt[i]){ 125 cnt[i]--; 126 if(ck){l[i]=j; ck=0;} 127 a[j++]=i; 128 } 129 if(!ck) r[i]=j-1; 130 } 131 st=(1<<n)-1; 132 for(int i=st;i>=0;i--) f[i]=INF; 133 f[st]=0; 134 for(int i=st;i;i--) if(hf(i)){ 135 if(i==2){ 136 f[st]=0; 137 } 138 for(int j=1;j<=N;j++){ 139 int y=dan(i,j); 140 if(y!=st) f[y]=min(f[y],f[i]+1); 141 } 142 for(int j=1;j<=N;j++){ 143 int y=dui(i,j); 144 if(y!=st) f[y]=min(f[y],f[i]+1); 145 } 146 for(int j=1;j<=N;j++){ 147 int y=san(i,j); 148 if(y!=st) f[y]=min(f[y],f[i]+1); 149 } 150 for(int j=1;j<N;j++){ 151 int y=zha(i,j); 152 if(y!=st) f[y]=min(f[y],f[i]+1); 153 } 154 for(int j=1;j<=N;j++) if(l[j]!=-1&&(r[j]-l[j]>1)){ 155 for(int k=1;k<=N;k++) if(l[k]!=-1){ 156 int y=sandaiyi(i,j,k); 157 if(y!=st) f[y]=min(f[y],f[i]+1); 158 } 159 } 160 for(int j=1;j<=N;j++) if(l[j]!=-1&&(r[j]-l[j]>1)){ 161 for(int k=1;k<=N;k++) if(l[k]!=-1){ 162 int y=sandaier(i,j,k); 163 if(y!=st) f[y]=min(f[y],f[i]+1); 164 } 165 } 166 for(int j=1;j<N;j++) if(l[j]!=-1){ 167 for(int k=j+4;k<=N-2;k++) if(l[k]!=-1){ 168 int y=shunzi(i,j,k); 169 if(y!=st) f[y]=min(f[y],f[i]+1); 170 } 171 } 172 for(int j=1;j<N;j++) if(l[j]!=-1&&(r[j]-l[j]>0)){ 173 for(int k=j+2;k<=N-2;k++) if(l[k]!=-1&&(r[k]-l[k]>0)){ 174 int y=liandui(i,j,k); 175 if(y!=st) f[y]=min(f[y],f[i]+1); 176 } 177 } 178 for(int j=1;j<N;j++) if(l[j]!=-1&&(r[j]-l[j]>1)){ 179 for(int k=j+1;k<=N-2;k++) if(l[k]!=-1&&(r[k]-l[k]>1)){ 180 int y=sanshun(y,j,k); 181 if(y!=st) f[y]=min(f[y],f[i]+1); 182 } 183 } 184 for(int j=1;j<=N;j++) if(l[j]!=-1&&(r[j]-l[j]>2)){ 185 for(int k=1;k<=N;k++) if(l[k]!=-1){ 186 for(int L=1;L<=N;L++) if(l[L]!=-1){ 187 int y=sidaier(i,j,k,L); 188 if(y!=st) f[y]=min(f[y],f[i]+1); 189 } 190 } 191 } 192 for(int j=1;j<=N;j++) if(l[j]!=-1&&(r[j]-l[j]>2)){ 193 for(int k=1;k<=N;k++) if(l[k]!=-1){ 194 for(int L=1;L<=N;L++) if(l[L]!=-1){ 195 int y=sidaidui(i,j,k,L); 196 if(y!=st) f[y]=min(f[y],f[i]+1); 197 } 198 } 199 } 200 } 201 printf("%d ",f[0]); 202 } 203 204 int main(){ 205 freopen("landlords.in","r",stdin); 206 freopen("landlords.out","w",stdout); 207 int cas; scanf("%d%d",&cas,&n); 208 while(cas--) Main(); 209 }
事实证明我想多了...
直接上爆搜,暴力枚举单顺,双顺和三顺,剩下的牌直接贪心(即按四带二,四带一对,四代两对,三带一,三代二,炸弹,三条,对子,单牌的顺序出,不难看出这么出牌是最优的,即出牌次数取决于顺的选择方式)。
时间复杂度O(玄学) ,所有点本地0.01s内跑出
代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define M 100 5 #define N 14 6 using namespace std; 7 int n,ans=10; 8 int a[M]={0},c[M]={0}; 9 10 int get(){ 11 c[0]=c[1]=c[2]=c[3]=c[4]=0; 12 for(int i=1;i<=N;i++) c[a[i]]++; 13 int sum=0; 14 while(c[4]&&c[2]>=2) c[4]--,c[2]-=2,sum++; 15 while(c[4]&&c[1]>=2) c[4]--,c[1]-=2,sum++; 16 while(c[4]&&c[2]) c[4]--,c[2]--,sum++; 17 while(c[3]&&c[2]) c[3]--,c[2]--,sum++; 18 while(c[3]&&c[1]) c[3]--,c[1]--,sum++; 19 return sum+c[1]+c[2]+c[3]+c[4]; 20 } 21 22 void dfs(int x){ 23 if(x>=ans) return; 24 ans=min(ans,x+get()); 25 for(int i=1;i<=8;i++){ 26 if(a[i]==0||a[i+1]==0||a[i+2]==0||a[i+3]==0) continue; 27 for(int j=i+4;j<=12;j++) if(a[j]==0) break; 28 else{ 29 for(int k=i;k<=j;k++) a[k]--; 30 dfs(x+1); 31 for(int k=i;k<=j;k++) a[k]++; 32 } 33 } 34 for(int i=1;i<=10;i++){ 35 if(a[i]<2||a[i+1]<2) continue; 36 for(int j=i+2;j<=12;j++) if(a[j]<2) break; 37 else{ 38 for(int k=i;k<=j;k++) a[k]-=2; 39 dfs(x+1); 40 for(int k=i;k<=j;k++) a[k]+=2; 41 } 42 } 43 for(int i=1;i<=11;i++){ 44 if(a[i]<3) continue; 45 for(int j=i+1;j<=12;j++) if(a[j]<3) break; 46 else{ 47 for(int k=i;k<=j;k++) a[k]-=3; 48 dfs(x+1); 49 for(int k=i;k<=j;k++) a[k]+=3; 50 } 51 } 52 } 53 54 int main(){ 55 freopen("landlords.in","r",stdin); 56 freopen("landlords.out","w",stdout); 57 int cas; cin>>cas>>n; 58 while(cas--){ 59 memset(a,0,sizeof(a)); 60 for(int i=1;i<=n;i++){ 61 int x,k; scanf("%d%d",&x,&k); 62 if(x<3){if(x==0) x=2; else if(x==2) x=1; else x=0;} 63 x=1+(x-3+N)%N; a[x]++; 64 } 65 ans=100; dfs(0); 66 printf("%d ",ans); 67 } 68 }