题目:在非负数组(乱序)中找到最小的可分配的id(从1开始编号),数据量10000000。
题目解读:在一个不重复的乱序的自然数组中找到最小的缺失的那个数,比如1,2,3,6,4,5,8,11。那么最小可用id就为7。
代码:
import java.util.Arrays; /** * 解决最小可用id问题 */ public class MinFreeId { public static void main(String[] args) { // int[]arr = {1,5,3,2,6,7,10,9,4}; // 最开始小数据测试 int []arr = new int[1000*1000]; for (int i = 0; i < arr.length; i++) { // if(i==900000) 那解法一运行时间就太长了 if (i==90000) { arr[i] = arr.length+10; }else { arr[i] = i+1; } } long now = System.currentTimeMillis(); System.out.println(find1(arr)); System.out.println("解法一消耗的时间:"+(System.currentTimeMillis()-now)+"ms"); now = System.currentTimeMillis(); System.out.println(find2(arr)); System.out.println("解法二消耗的时间:"+(System.currentTimeMillis()-now)+"ms"); now = System.currentTimeMillis(); System.out.println(find3(arr)); System.out.println("解法三消耗的时间:"+(System.currentTimeMillis()-now)+"ms"); now = System.currentTimeMillis(); System.out.println(find4(arr,0,arr.length-1)); System.out.println("解法四消耗的时间:"+(System.currentTimeMillis()-now)+"ms"); } // O(n^2) 暴力解法:从1开始依次探测每个自然数是否在数组中 static int find1(int[]arr){ int i = 1; while(true){ for (int j = 0; j < arr.length;) { if (arr[j]==i) { i++; j = 0; continue; }else { j++; } } return i; } } // O(nlgn) static int find2(int[]arr){ Arrays.sort(arr); // O(nlgn) 后续扫描时间O(N) 相比之下 取O(nlgn) 所以时间复杂度为O(nlgn) int i = 0; while(i<arr.length){ if (i+1!=arr[i]) { // 不存在的最小自然数 return i+1; } i++; } return i+1; } /** * 改进1:用辅助空间 * 有点类似计数排序 O(N)但是浪费空间 */ static int find3(int[]arr){ int n = arr.length; int []helper = new int[n+1]; for (int i = 0; i < n; i++) { // O(N) if (arr[i]<n+1) { helper[arr[i]] = 1; // 辅助空间的下标也是有用的 } } for (int i = 1; i <= n; i++) { // O(N) if (helper[i] == 0) { return i; } } return n+1; } /** * // O(N) * 改进2:分区,递归 * 问题可转化为:n的正数的数组A,如果存在小于n的数不在数组中,必然存在大于n的数组中,否则数组排列恰好为1到n */ private static int find4(int[] arr, int l, int r) { if (l>r) { return l+1; } int midIndex = l+((r-l)>>1); // 中间下标 int q = SelectK.selectK(arr, l, r, midIndex-l+1); // 调用查找第k大的元素的方法 int t = midIndex + 1; // 期望值 if (q==t) { // 左侧紧密 return find4(arr,midIndex+1,r); }else { // 左侧稀疏 return find4(arr, l, midIndex-1); } } }
结果:
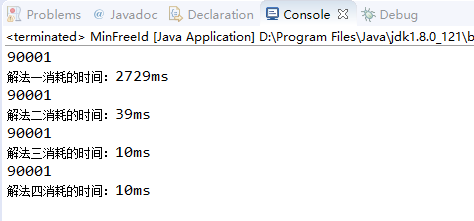
结论:根据每个解法所消耗的时间即可得出哪个解法的效率更高。所以在数据量较大的情况下最好选用O(lgn)和O(N)级别的算法,O(nlgn)次之。