Raster是个啥子东西
现如今,不仅是在遥感应用中能看到花花绿绿的影像了,在GIS应用中也能随处看到她们的身影。在各种在线地图中,卫星影像作为底图与矢量的道路层叠加;高程DEM作为高程来源实现地形的山影效果。相信大家对影像这个词,应该一点儿也不感到陌生。
那么栅格呢?相对与我们熟悉的影像,这俩只是名词上的区别么?
栅格(Raster)和影像(Images/Imagery)在GIS应用中经常被相互指代。如果非要区别一下呢,影像是指通过各种遥感设备,传感器,或者照相机得到的电子的或者纸质的图片,栅格则是一种数据模型,用来特指影像存储方式的。类比一下,如果把ArcGIS中存储显示的图片都称之为酒的话,栅格就是酒瓶,而影像就是瓶中的美酒了。
咱们再来仔细看看栅格数据。
如果说使用矢量来描绘我们的世界,需要使用到点,线或者是面。而构成点,线,或者面的最小单元,是点(结点)。那么另外一种用于描绘地物的数据-栅格的最小单元又是什么呢?
如果你曾经好奇的把影像/栅格数据放大放大再放大,那么可能会注意到,当放大到某一个层级后,栅格数据就会变成下图所示的状态,变成了一个个的小格子。这些小格子,就是栅格数据的最小单元,Cell,也叫像元。对影像来说,这个最小的单元被叫做pixel,像素。
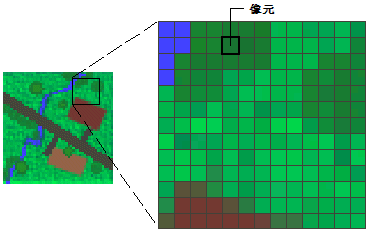
熟悉shape格式的筒子们都知道,线或者面数据都是通过点串来存储的。打开属性表也能够看到,撇开业务属性,就空间属性而言,每一条线就是一条记录,而这条记录中存储的shape再展开来才是构成这条线的点串的坐标(xy坐标)。而栅格数据的组织方式就非常的简单,有多简单呢,它就是一矩阵!栅格/影像数据看起来很复杂,还那么大一块,但是其实就是按行和列存储的像元。栅格运算的时候与矩阵运算是一样的,找到相应的位置,然后将象元值进行相应的加减乘除就可以了。
通过矩阵方式存储的栅格数据有显而易见的优点,数据结构简单。矢量的点,线,面也可以存储在栅格数据中,这样更方便参与空间分析的运算。BUT,将地物都栅格化了存储也有自己的弊端的。首先,栅格化之后,数据的精度取决于且仅取决于栅格的象元大小。象元越小,数据的所占的磁盘空间越大,处理起来越慢。再有呢,就是栅格的最小单元是不能够再分割的,在数据存储或者重建的时候会有误差。例如像元大小为1m的栅格是不能精确存储边长为10.5m的矢量边的。
正如上面提到的,像元有个不能被改变的特性,就是它是一个正方形,长 = 宽 = 像元大小 = 格网大小(栅格) = 分辨率(影像)。对于一个栅格来说,长与宽可以不同,说明栅格的行数与列数不等,也就是每一行的像元数与每一列的像元数不等。但是在一个栅格数据中,像元大小是一定的。
象元值又代表了什么呢?
如果需要了解一个矢量数据的属性,我们Identify一下,就可以看到该矢量背后的故事。这个多边形代表的是那个省,这个省的人口有多少,编码是什么等等等等。那么我们Identify一下栅格的某个位置,得到的RGB的值表示又是什么意思呢?
小时候的自然课应该也有讲过,世间万物对不同光的吸收和反射是不同的。而我们看到的影像,就是通过传感器记录下每一个位置对红光(Red),绿光(Green)和蓝光(Blue)的反射值得到的。(高级传感器例如卫星上用的还记录了更多光波段的反射值,这里不罗嗦了)栅格数据中,代表实际“属性”的像元值就是反射值。
当然了,反射值只是针对航片,卫片和照片的。对于DEM或者其他高程影像来说,像元值代表的就是该位置的实际高度。而土地分类图中每一个像元值代表的是该位置上的土地利用类型。
还有一个问题,就是如果栅格都是矩阵,那么为什么会有离散数据(Discrete Data)和连续数据(Continues Data)的区别?
这个是由于栅格数据所表现的事物类型是多种多样的。根据栅格中像元值的分布类型,将他们分成了3类,离散数据(有时也叫专题数据),主要是指分类结果数据,例如土地利用图;连续数据,一般是真实地物的直接体现,比如各种遥感影像,DEM,温度图等等等等;最后一类是图片,例如扫描地图或者楼房照片等。
预告一下,下一贴要讲讲像元深度(pixel depth),波段等属性信息。