二叉树
二叉树的特点:①每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点。
②左子树和右子树是有顺序的,次序不能任意颠倒。
③即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。
1. 二叉树的顺序存储结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点。结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等。
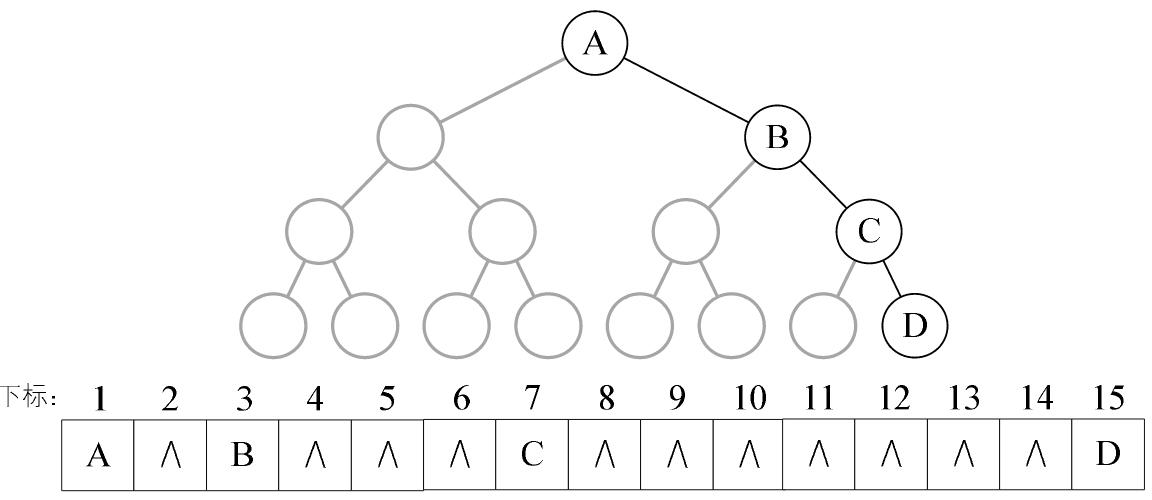
But,考虑一种极端的情况,一棵深度为k的右斜树,它只有k个结点,却需要分配2的k次方-1个存储单元空间,这显然是对存储空间的浪费,所以,顺序存储结构一般只适用于完全二叉树。
2. 二叉树的链式存储结构
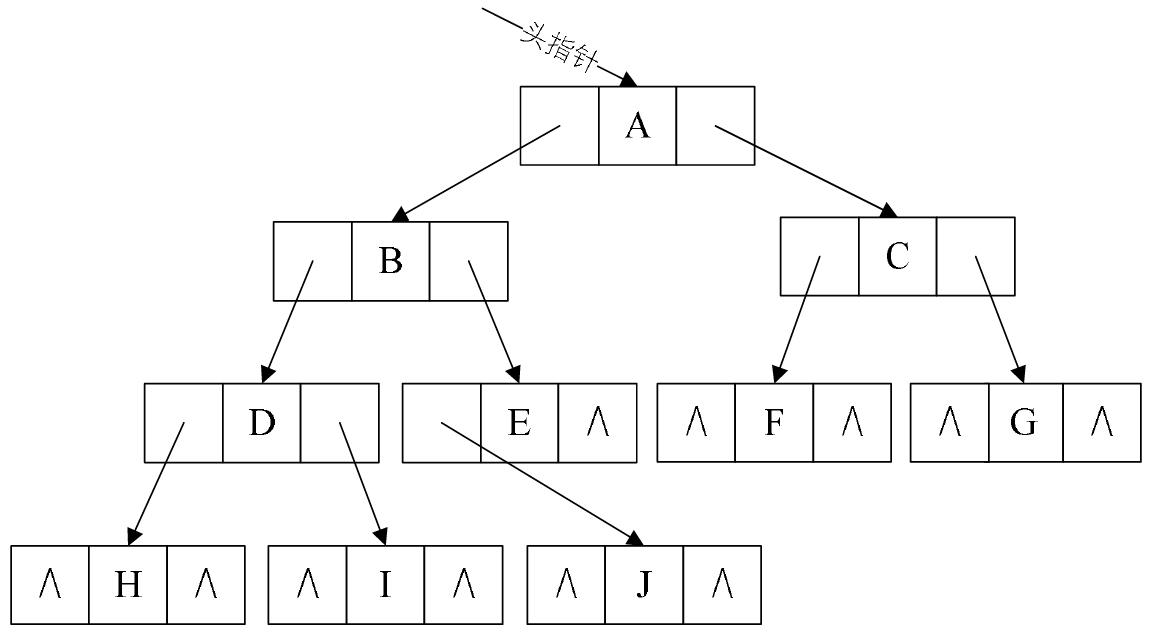
既然顺序存储适用性不强,我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。其中data是数据域,lchild和rchild都是指针域,分别存放指向左孩子和右孩子的指针。
二叉查找树
二叉查找树(Binary Search Tree),又称为二叉搜索树。设x为二叉查找树中的一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
(01) 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(02) 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点(no duplicate nodes)。
1. 二叉搜索树结点结构
二叉查找树的节点包含的基本信息:
(01) key -- 它是关键字,是用来对二叉查找树的节点进行排序的。
(02) left -- 它指向当前节点的左孩子。
(03) right -- 它指向当前节点的右孩子。
(04) parent -- 它指向当前节点的父结点。
typedef int T; typedef struct BSTreeNode { T key; BSTreeNode *left; BSTreeNode *right; BSTreeNode *parent; }
2. 二叉搜索树树创建
// 二叉查找树的创建 Node* create_bstree_node(T key, Node *parent, Node *left, Node* right) { Node* p; if ((p = (Node *)malloc(sizeof(Node))) == NULL) return NULL; p->key = key; p->left = left; p->right = right; p->parent = parent; return p; }
3. 二叉搜索树树插入
// 插入结点,可插入相同结点 Node* bstree_insert(Node *pNode, Node *pInsertNode) { Node *pFindParentNode = NULL; // 找到pInsertNode的父节点结点 Node *pTempNode = pNode; while(pTempNode != NULL) { pFindParentNode = pTempNode; if (pInsertNode->key > pTempNode->key) { pTempNode = pTempNode->right; } else if (pInsertNode->key < pTempNode->key) { pTempNode = pTempNode->left; } else { // 若插入的结点和树中的结点相同,则释放刚申请的插入结点控件 free(pInsertNode); return pNode; } } pInsertNode->parent = pFindParentNode; if (pFindParentNode == NULL) // 当树为空的时候 { pNode = pInsertNode; } // 当找到父节点时,无法判断是比父节点小孩是大 else if (pInsertNode->key < pFindParentNode->key) { pFindParentNode->left = pInsertNode; } else { pFindParentNode->right = pInsertNode; } return pNode; } // 插入结点,可插入相同结点 Node* insert_bstree(Node *pNode, T key) { Node *pNewNode = create_bstree_node(key, NULL, NULL, NULL); if (pNewNode == NULL) { return pNode; } return bstree_insert(pNode, pNewNode); }
4. 二叉搜索树树遍历
二叉树的遍历分三种:前序遍历,中序遍历,后续遍历
(1)前序遍历
若二叉树非空,则执行以下操作:
(01) 访问根结点;
(02) 先序遍历左子树;
(03) 先序遍历右子树。
void preorder_bstree(Node *pNode) { if (NULL != pNode) { cout << pNode->key << " "; preorder_bstree(pNode->left); preorder_bstree(pNode->right); } }
(2)中序遍历
若二叉树非空,则执行以下操作:
(01) 中序遍历左子树;
(02) 访问根结点;
(03) 中序遍历右子树。
void midorder_bstree(Node *pNode) { if (NULL != pNode) { midorder_bstree(pNode->left); cout << pNode->key<< " "; midorder_bstree(pNode->right); } }
(3)后续遍历
若二叉树非空,则执行以下操作:
(01) 后序遍历左子树;
(02) 后序遍历右子树;
(03) 访问根结点。
void postorder_bstree(Node *pNode) { if (NULL != pNode) { postorder_bstree(pNode->left); postorder_bstree(pNode->right); cout << pNode->key<< " "; } }
5. 二叉搜索树查找
Node* bstree_search(Node* pNode, T key) { if (NULL == pNode || pNode->key == key) { return pNode; } if (pNode->key > key) { return bstree_search(pNode->left, key); } else { return bstree_search(pNode->right, key); } }
6. 二叉搜索树树最大值
// 查找最大值:一直遍历右子树 Node* bstree_maximum(Node *pNode) { if (pNode == NULL) { return NULL; } while(pNode->right != NULL) { pNode = pNode->right; } return pNode; }
7. 二叉搜索树树最小值
// 查找最小值:一直遍历左子树 Node* bstree_minimum(Node *pNode) { if (pNode == NULL) { return NULL; } while(pNode->left != NULL) { pNode = pNode->left; } return pNode; }
8. 查找结点的后继结点
节点的后继:是该节点的右子树中的最小节点。
Node* bstree_successor(Node *pNode) { // 若存在右子树,则前驱结点为其右子树中最小结点 // 若没有右子树,则分两种情况,判断该结点为左结点还是右结点 // (1) 若为左结点,则它的父结点即为其后继结点 // (2) 若为右结点,则其后继结点为其最低父结点 if (pNode != NULL || pNode->right != NULL) { return bstree_minimum(pNode->right); } Node* pParent = pNode->parent; while (pParent != NULL && (pParent->right == pNode)) { pNode = pParent; pParent = pParent->parent; } return pParent; }
9. 查找结点的前驱结点
节点的前驱:是该节点的左子树中的最大节点
Node* bstree_successor(Node *pNode) { // 若存在右子树,则前驱结点为其右子树中最小结点 // 若没有右子树,则分两种情况,判断该结点为左结点还是右结点 // (1) 若为左结点,则它的父结点即为其后继结点 // (2) 若为右结点,则其后继结点为其最低父结点 if (pNode != NULL || pNode->right != NULL) { return bstree_minimum(pNode->right); } Node* pParent = pNode->parent; while (pParent != NULL && (pParent->right == pNode)) { pNode = pParent; pParent = pParent->parent; } return pParent; }
10. 删除节点
// 删除节点 // 若结点为叶子节点直接删除该节点 // 若该节点为单支结点(即只有左子树或右子树),则让该节点的父节点和其子树相连 // 若该节点既有左子树又有右子树 // 找到该节点的后继结点p,该后继结点p肯定没左子树, // 将左子树的父节点指向p结点的父节点并将p节点的值给该节点 Node* bstree_delete(Node *pNode, Node *pDeleteNode) { if (pNode == NULL || pDeleteNode == NULL) { return pNode; } // 该节点的左右结点都为空 if ((pDeleteNode->left == NULL) && (pDeleteNode->right == NULL)) { if (pDeleteNode == pNode) { pNode = NULL; } if (pDeleteNode->parent->left == pDeleteNode) { pDeleteNode->parent->left = NULL; } else if (pDeleteNode->parent->right == pDeleteNode) { pDeleteNode->parent->right = NULL; } } // 该节点的左右结点有一个为空 else if ((pDeleteNode->left == NULL) || (pDeleteNode->right == NULL)) { if (pDeleteNode == pNode) { if (pDeleteNode->left != NULL) { pDeleteNode->left->parent = NULL; } else if (pDeleteNode->right != NULL) { pDeleteNode->right->parent = NULL; } } else { if (pDeleteNode == pDeleteNode->parent->left && pDeleteNode->left != NULL) { pDeleteNode->parent->left = pDeleteNode->left; } else if (pDeleteNode == pDeleteNode->parent->left && pDeleteNode->right != NULL) { pDeleteNode->parent->left = pDeleteNode->right; } else if (pDeleteNode == pDeleteNode->parent->right && pDeleteNode->left != NULL) { pDeleteNode->parent->right = pDeleteNode->left; } if (pDeleteNode == pDeleteNode->parent->right && pDeleteNode->right != NULL) { pDeleteNode->parent->right = pDeleteNode->right; } } } // 该节点的左右结点都存在 else { Node *pSuccessorNode = bstree_successor(pDeleteNode); // 找到后继结点,后继结点一定没有左子树 pDeleteNode->key = pSuccessorNode->key; if (pSuccessorNode->right != NULL) { pSuccessorNode->right->parent = pSuccessorNode->parent; } if (pSuccessorNode == pSuccessorNode->parent->left) { pSuccessorNode->parent->left = NULL; } else { pSuccessorNode->parent->right = NULL; } pDeleteNode = pSuccessorNode; } free(pDeleteNode); pDeleteNode = NULL; return pNode; } Node* delete_bstree(Node* pNode, T key) { Node *pSearchNode = bstree_search(pNode, key); if (pSearchNode != NULL) { pNode = bstree_delete(pNode, pSearchNode); } return pNode; }
11. 删除二叉搜索树
void destroy_bstree(Node *pNode) { if (pNode==NULL) return ; if (pNode->left != NULL) destroy_bstree(pNode->left); if (pNode->right != NULL) destroy_bstree(pNode->right); free(pNode); }
12. 打印二叉搜索树
void print_bstree(Node *pNode, T key, int direction) { if(pNode != NULL) { if(direction==0) // tree是根节点 printf("%2d is root ", pNode->key); else // tree是分支节点 printf("%2d is %2d's %6s child ", pNode->key, key, direction==1?"right" : "left"); print_bstree(pNode->left, pNode->key, -1); print_bstree(pNode->right,pNode->key, 1); } }
13. 实现代码测试

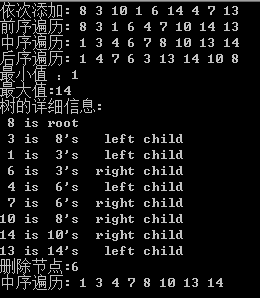
#include "stdio.h" #include <iostream> #include <stack> using namespace std; typedef int T; typedef struct BSTreeNode { T key; BSTreeNode *left; BSTreeNode *right; BSTreeNode *parent; }Node; // 二叉查找树的创建 Node* create_bstree_node(T key, Node *parent, Node *left, Node* right) { Node* p; if ((p = (Node *)malloc(sizeof(Node))) == NULL) return NULL; p->key = key; p->left = left; p->right = right; p->parent = parent; return p; } // 二叉查找树的遍历 // 前序遍历 void preorder_bstree(Node *pNode) { if (NULL != pNode) { cout << pNode->key << " "; preorder_bstree(pNode->left); preorder_bstree(pNode->right); } } // 中序遍历 void midorder_bstree(Node *pNode) { if (NULL != pNode) { midorder_bstree(pNode->left); cout << pNode->key<< " "; midorder_bstree(pNode->right); } } // 后序遍历 void postorder_bstree(Node *pNode) { if (NULL != pNode) { postorder_bstree(pNode->left); postorder_bstree(pNode->right); cout << pNode->key<< " "; } } // 查找 Node* bstree_search(Node* pNode, T key) { if (NULL == pNode || pNode->key == key) { return pNode; } if (pNode->key > key) { return bstree_search(pNode->left, key); } else { return bstree_search(pNode->right, key); } } // 查找最大值:一直遍历右子树 Node* bstree_maximum(Node *pNode) { if (pNode == NULL) { return NULL; } while(pNode->right != NULL) { pNode = pNode->right; } return pNode; } // 查找最小值:一直遍历左子树 Node* bstree_minimum(Node *pNode) { if (pNode == NULL) { return NULL; } while(pNode->left != NULL) { pNode = pNode->left; } return pNode; } // 查找后继结点 Node* bstree_successor(Node *pNode) { // 若存在右子树,则前驱结点为其右子树中最小结点 // 若没有右子树,则分两种情况,判断该结点为左结点还是右结点 // (1) 若为左结点,则它的父结点即为其后继结点 // (2) 若为右结点,则其后继结点为其最低父结点 if (pNode != NULL || pNode->right != NULL) { return bstree_minimum(pNode->right); } Node* pParent = pNode->parent; while (pParent != NULL && (pParent->right == pNode)) { pNode = pParent; pParent = pParent->parent; } return pParent; } // 查找前驱结点 // 若存在左子树,即为左子树中的最大节点 // 若不存在左子树,则分两种情况,判断该结点为左结点还是右节点 // (1)若为左子树,则它的父节点就是其前驱结点 // (2)若为右子树,则其前驱结点为其最低父结点 Node* bstree_predecessor(Node *pNode) { if (pNode != NULL && pNode->left) { return bstree_maximum(pNode->left); } Node *pParent = pNode->parent; while (pParent != NULL &&(pParent->right == pNode)) { pNode = pParent; pParent = pParent->parent; } return pParent; } // 插入结点,可插入相同结点 Node* bstree_insert(Node *pNode, Node *pInsertNode) { Node *pFindParentNode = NULL; // 找到pInsertNode的父节点结点 Node *pTempNode = pNode; while(pTempNode != NULL) { pFindParentNode = pTempNode; if (pInsertNode->key > pTempNode->key) { pTempNode = pTempNode->right; } else if (pInsertNode->key < pTempNode->key) { pTempNode = pTempNode->left; } else { // 若插入的结点和树中的结点相同,则释放刚申请的插入结点控件 free(pInsertNode); return pNode; } } pInsertNode->parent = pFindParentNode; if (pFindParentNode == NULL) // 当树为空的时候 { pNode = pInsertNode; } // 当找到父节点时,无法判断是比父节点小孩是大 else if (pInsertNode->key < pFindParentNode->key) { pFindParentNode->left = pInsertNode; } else { pFindParentNode->right = pInsertNode; } return pNode; } // 插入结点,可插入相同结点 Node* insert_bstree(Node *pNode, T key) { Node *pNewNode = create_bstree_node(key, NULL, NULL, NULL); if (pNewNode == NULL) { return pNode; } return bstree_insert(pNode, pNewNode); } // 删除节点 // 若结点为叶子节点直接删除该节点 // 若该节点为单支结点(即只有左子树或右子树),则让该节点的父节点和其子树相连 // 若该节点既有左子树又有右子树 // 找到该节点的后继结点p,该后继结点p肯定没左子树, // 将左子树的父节点指向p结点的父节点并将p节点的值给该节点 Node* bstree_delete(Node *pNode, Node *pDeleteNode) { if (pNode == NULL || pDeleteNode == NULL) { return pNode; } // 该节点的左右结点都为空 if ((pDeleteNode->left == NULL) && (pDeleteNode->right == NULL)) { if (pDeleteNode == pNode) { pNode = NULL; } if (pDeleteNode->parent->left == pDeleteNode) { pDeleteNode->parent->left = NULL; } else if (pDeleteNode->parent->right == pDeleteNode) { pDeleteNode->parent->right = NULL; } } // 该节点的左右结点有一个为空 else if ((pDeleteNode->left == NULL) || (pDeleteNode->right == NULL)) { if (pDeleteNode == pNode) { if (pDeleteNode->left != NULL) { pDeleteNode->left->parent = NULL; } else if (pDeleteNode->right != NULL) { pDeleteNode->right->parent = NULL; } } else { if (pDeleteNode == pDeleteNode->parent->left && pDeleteNode->left != NULL) { pDeleteNode->parent->left = pDeleteNode->left; } else if (pDeleteNode == pDeleteNode->parent->left && pDeleteNode->right != NULL) { pDeleteNode->parent->left = pDeleteNode->right; } else if (pDeleteNode == pDeleteNode->parent->right && pDeleteNode->left != NULL) { pDeleteNode->parent->right = pDeleteNode->left; } if (pDeleteNode == pDeleteNode->parent->right && pDeleteNode->right != NULL) { pDeleteNode->parent->right = pDeleteNode->right; } } } // 该节点的左右结点都存在 else { Node *pSuccessorNode = bstree_successor(pDeleteNode); // 找到后继结点,后继结点一定没有左子树 pDeleteNode->key = pSuccessorNode->key; if (pSuccessorNode->right != NULL) { pSuccessorNode->right->parent = pSuccessorNode->parent; } if (pSuccessorNode == pSuccessorNode->parent->left) { pSuccessorNode->parent->left = NULL; } else { pSuccessorNode->parent->right = NULL; } pDeleteNode = pSuccessorNode; } free(pDeleteNode); pDeleteNode = NULL; return pNode; } Node* delete_bstree(Node* pNode, T key) { Node *pSearchNode = bstree_search(pNode, key); if (pSearchNode != NULL) { pNode = bstree_delete(pNode, pSearchNode); } return pNode; } // 打印二叉树 void print_bstree(Node *pNode, T key, int direction) { if(pNode != NULL) { if(direction==0) // tree是根节点 printf("%2d is root ", pNode->key); else // tree是分支节点 printf("%2d is %2d's %6s child ", pNode->key, key, direction==1?"right" : "left"); print_bstree(pNode->left, pNode->key, -1); print_bstree(pNode->right,pNode->key, 1); } } void destroy_bstree(Node *pNode) { if (pNode==NULL) return ; if (pNode->left != NULL) destroy_bstree(pNode->left); if (pNode->right != NULL) destroy_bstree(pNode->right); free(pNode); } static int arr[]= {8,3,10,1,6,14,4,7,13}; #define TBL_SIZE(a) ( (sizeof(a)) / (sizeof(a[0])) ) void main() { Node *root = NULL; cout << "依次添加: "; int nlen = TBL_SIZE(arr); for(int i=0; i<nlen; i++) { cout << arr[i] << " "; root = insert_bstree(root, arr[i]); } cout << endl; cout << "前序遍历: "; preorder_bstree(root); cout << endl; cout << ("中序遍历: "); midorder_bstree(root); cout << endl; cout << ("后序遍历: "); postorder_bstree(root); cout << endl; cout<< "最小值 :" << bstree_minimum(root)->key << endl; cout << "最大值:" << bstree_maximum(root)->key << endl; cout << "树的详细信息:" << endl; print_bstree(root, root->key, 0); cout <<"删除节点:"<< 6 <<endl; root = delete_bstree(root, 6); cout <<"中序遍历: "; midorder_bstree(root); cout << endl; // 销毁二叉树 destroy_bstree(root); return; }