CF607B Zuma 题解

CF607B Zuma 题解

间隙(原题面)

• 前排声明:蒟蒻刚学oi没多久,而且是自学的,写的可能会比较累赘,望见谅。

前置知识

• 基础区间dp

题意

给一个长度为n的串,每次都可以挑选一个回文的连续字串进行消除,删除后，剩余的串将连接在一起，形成一个新的串,求把串全部删除完需要的最小次数

---

分析

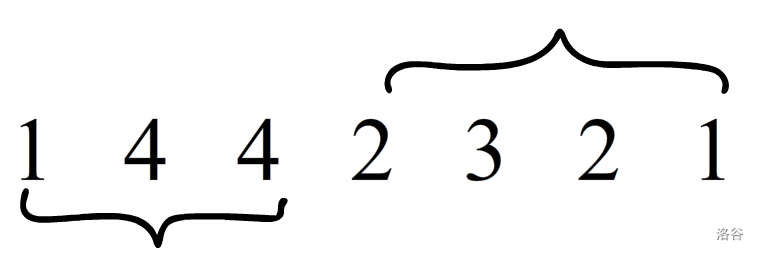
可以看出每一个区间的的求解都可以分为更小的两个区间的求解

联想到区间dp

设(dp[l][r])为左端点为l,右端点为r时的最优解

不难推出比较套路的状态转移方程

• (dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]).(l<=k<r))

同时,这里还有一个区间的回文判断

假设我们把总区间划分为两个区间

([1,4,5,3,4,1,3,2])和([3,2])

其中([1,4,5,3,4,1,3,2])包含一个回文部分

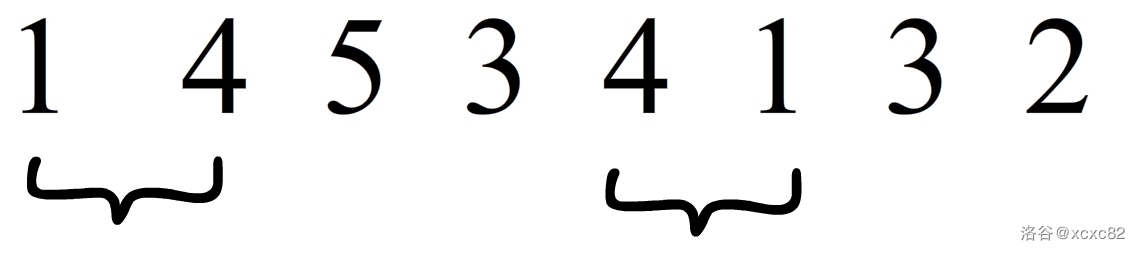
此时我们只要直接将回文部分删去即可

即(dp[l][r]=dp[l+1][r-1])

这其实是一个类似于预处理的东西(个人看法,可能有误)

如果一个区间包含回文部分

则先把(dp[l][r])给预处理成它不进行划分可以产生的最小值

再去和划分成两个区间所产生的最小值进行比较

• 即(if(a[l]==a[r]))
  (dp[l[[r]=dp[l+1][r-1])

贴上丑陋的代码

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
const int MAXN = 510;
int n,a[MAXN],dp[MAXN][MAXN];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++){//预处理长度为1的区间
		dp[i][i]=1;
	}
	for(int len=1;len<n;len++){//枚举长度
		for(int l=1;l<=n&&l+len<=n;l++){//枚举左右断点
		
			int r=l+len;
				dp[l][r]=inf;
			if(a[l]==a[r]){//如果包含回文部分
				if(r==l+1){//注意,这里是区间长度为2的特判
					dp[l][r]=dp[l+1][r-1]=1;
				}
				else dp[l][r]=dp[l+1][r-1];
			}
			for(int k=l;k<r;k++){//枚举断点
				dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]);
			}
		}
	}
	cout<<dp[1][n];
} 

如有错误欢迎大佬们指出QwQ