题意:给定一个序列A,接下来又m个询问,每个询问输出A[L,R]中的第K大。(保证第k大存在)
思路:
我想拿来练习“可持久化线段树”的,搜到这个比较巧的算法也可以解决这个问题,叫“归并树?。大概的思想就是和线段树一样,只是线段树上的每个非叶子节点是一个区间,等于该节点的两个孩子节点的区间的拼接起来,而每个区间内保持有序的。那么在查找时就找到这两个区间,二分枚举答案然后在询问区间[L,R]判断否排第k。这里二分答案只需要在线段树的根进行就行了,因为根这个区间是有序的。查找时[L,R]可能会是两个区间的拼接的[L,mid]+[mid+1,R],所以要在两个区间中分别判断val排行老几,然后加起来就是其在[L,R]的真实排行了,这可以用low_bound函数实现。

1 //#include <bits/stdc++.h> 2 #include <iostream> 3 #include <cstdio> 4 #include <cstring> 5 #include <map> 6 #include <vector> 7 #include <algorithm> 8 #include <iostream> 9 #define pii pair<int,int> 10 #define INF 0x3f3f3f3f 11 #define LL long long 12 using namespace std; 13 const int N=100010; 14 int seq[N], tree[40][N]; 15 16 void build_tree(int L,int R,int depth) 17 { 18 if(L==R) 19 { 20 tree[depth][L]=seq[L]; 21 return; 22 } 23 int mid=(L+R)>>1; 24 build_tree(L,mid,depth+1); 25 build_tree(mid+1,R,depth+1); 26 27 //归并 28 int first=L, second=mid+1, cnt=L; 29 while( first<=mid && second<=R ) 30 { 31 if(tree[depth+1][first]<tree[depth+1][second]) 32 tree[depth][cnt++]=tree[depth+1][first++]; 33 else 34 tree[depth][cnt++]=tree[depth+1][second++]; 35 } 36 if(first<=mid) //左边未完 37 { 38 for(int i=first; i<=mid; i++) 39 tree[depth][cnt++]=tree[depth+1][i]; 40 } 41 else //右边未完 42 { 43 for(int i=second; i<=R; i++) 44 tree[depth][cnt++]=tree[depth+1][i]; 45 } 46 } 47 48 49 int query(int ll,int rr,int L,int R,int val,int depth) //返回val在[L,R]内的排名-1 50 { 51 if(L==ll && rr==R) 52 return lower_bound( &tree[depth][L], &tree[depth][R+1], val) 53 -&tree[depth][L]; 54 int mid=(ll+rr)>>1, cnt=0; 55 if( R<=mid ) cnt+=query(ll,mid, L,R, val,depth+1); 56 else if( L>mid ) cnt+=query(mid+1,rr, L,R, val,depth+1); 57 else 58 { 59 cnt+=query(ll,mid, L,mid, val,depth+1); 60 cnt+=query(mid+1,rr, mid+1,R, val,depth+1); 61 } 62 return cnt; 63 } 64 65 int main() 66 { 67 freopen("input.txt", "r", stdin); 68 int n, m, L, R, k; 69 while(~scanf("%d%d",&n,&m)) 70 { 71 for(int i=1; i<=n; i++) scanf("%d",&seq[i]); 72 build_tree(1, n, 0); 73 74 while(m--) 75 { 76 scanf("%d%d%d",&L,&R,&k); 77 k--; 78 int ll=1, rr=n; 79 while( ll<rr ) //在tree[0]中二分这个数 80 { 81 int mid=ll+(rr-ll+1)/2; 82 int pos=query(1,n, L,R, tree[0][mid],0); 83 if( pos<=k ) ll=mid; //所查找的数太小了 84 else rr=mid-1; 85 } 86 printf("%d ", tree[0][ll]); 87 } 88 } 89 return 0; 90 }
主席树解法:按照序列的顺序seq[i],每插入1个点就建1棵树,而每棵树中有且只有seq[1,i]这个序列,而且不是按照seq[1,i]的顺序,而是变成在该树中是有序的。
举例:假设有序列seq[4]={1,3,2,4}。
插入第seq[1]后的结果:

插入第seq[2]后的结果:
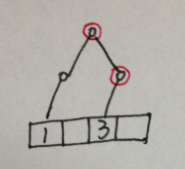
插入第seq[3]后的结果:

插入第seq[4]后的结果:
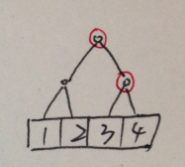
观察上面的4张图,红色的点表示是不同于上一幅图的的点,即是新创建的的点。可以看到,每次插入后最多仅有logn个点会被创建。插入是按照有序的方式插入的,比如新插入seq[2]=2,那么其应该排在第二,所以我们需要事先对seq进行排序,才能知道seq[i]的具体应该插在什么位置。
得到这些图就可以O(logN)知道第k个数了,比如要在区间[3,4]中找k=1的数字,那么只需要根据root[2]和root[4]就可以算出,只需要在每个节点上用个计数器cnt表示该子树的节点数,具体的话不难算的,自己研究下图吧。

1 //#include <bits/stdc++.h> 2 #include <iostream> 3 #include <cstdio> 4 #include <cstring> 5 #include <map> 6 #include <algorithm> 7 #include <vector> 8 #include <iostream> 9 #define pii pair<int,int> 10 #define INF 0x3f3f3f3f 11 #define LL long long 12 using namespace std; 13 const int N=100010; 14 struct Node 15 { 16 int L, R, cnt; 17 }nod[N*40]; //线段树上的节点 18 struct Seq 19 { 20 int val,idx; 21 bool operator < ( const Seq &t ) const{return val<t.val;} 22 }seq[N]; //序列 23 int rank[N], root[N], node_cnt; 24 25 void insert(int rk,int &t,int L,int R) //每次插入,就建1棵新树 26 { 27 nod[node_cnt]=nod[t]; 28 t=node_cnt++; 29 nod[t].cnt++; //此子树的叶子节点数 30 31 if(L==R) return ; //到底了。只存此子树的节点数 32 33 int mid=(L+R)>>1; 34 if(rk<=mid) insert(rk,nod[t].L, L,mid); 35 else insert(rk,nod[t].R, mid+1,R); 36 } 37 38 int query(int t1,int t2,int k,int L,int R) 39 { 40 if(L==R) return R; //返回的是“有序序列”的下标 41 int L1=nod[t1].L, L2=nod[t2].L; //两棵树的左子树节点数量 42 int left=nod[L2].cnt-nod[L1].cnt; //用于判断第k大在左/右 43 int mid=(L+R)>>1; 44 45 if(k<=left) query(nod[t1].L, nod[t2].L, k, L, mid); //在左边 46 else query(nod[t1].R, nod[t2].R, k-left, mid+1, R ); 47 } 48 49 int main() 50 { 51 //freopen("input.txt", "r", stdin); 52 int n, m, L, R, k; 53 while(~scanf("%d%d",&n,&m)) 54 { 55 node_cnt=1; 56 memset(root, 0, sizeof(root)); 57 for(int i=1; i<=n; i++) 58 { 59 scanf("%d",&seq[i].val); 60 seq[i].idx=i; 61 } 62 sort(seq+1,seq+n+1); //需先排序 63 for(int i=1; i<=n; i++) //反向索引 64 rank[ seq[i].idx ]=i; 65 for(int i=1; i<=n; i++) //按原序逐个插入 66 { 67 root[i]=root[i-1]; 68 insert(rank[i], root[i], 1, n); 69 } 70 while(m--) 71 { 72 scanf("%d%d%d",&L,&R,&k); 73 int idx=query(root[L-1], root[R], k, 1, n); //两树可以同时进行 74 printf("%d ", seq[idx].val); 75 } 76 } 77 return 0; 78 }
