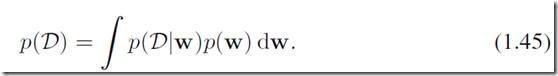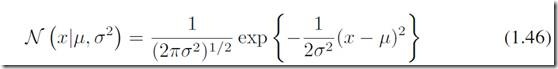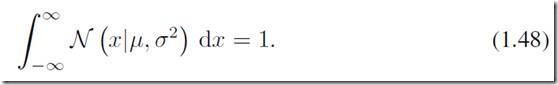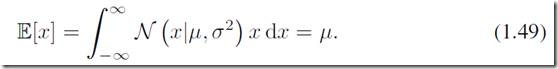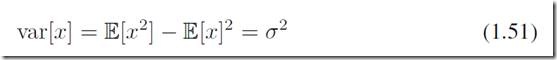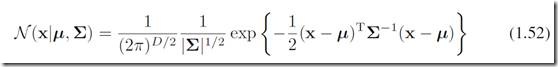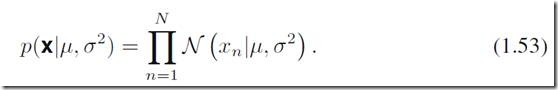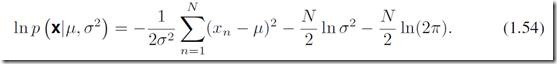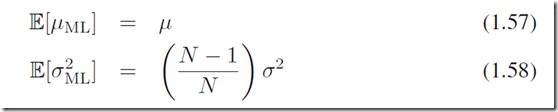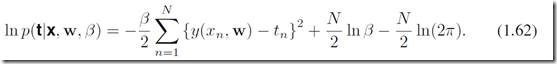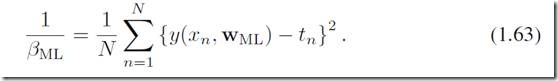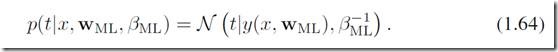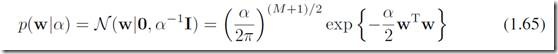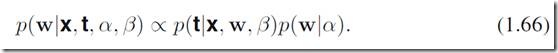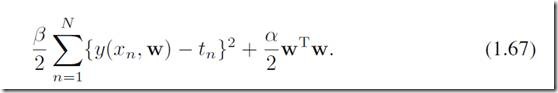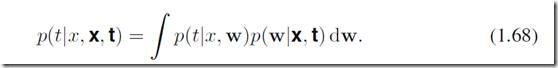今天开始学Pattern Recognition and Machine Learning (PRML)，章节1.2，Probability Theory （下）

今天开始学Pattern Recognition and Machine Learning (PRML)，章节1.2，Probability Theory （下）

今天把1.2写完，这一节讲了很多重要的基础内容。

1.2.3 贝叶斯概率

这一节的上半部分，我们结合一个盒子-水果抽取的问题，从随机可重复事件频率的角度理解了概率，这是经典的一种通过频率来理解概率的角度，接下来我们用贝叶斯角度来理解概率，重点关注不确定性。

有些事件称之为不确定事件，比如月亮是不是曾经围绕太阳旋转，北极的冰是否会在一百年后消失，这些事件都没办法通过重复事件来确定概率。但是我们可以通过其他一些手段来得到一些结果，比如我们可以通过观察每年冰层的消融比率来确定是否有可能消失。当然，人们会通过这些结果来指导未来的活动（decision），比如减少温室气体的排放，通过这些行为，我们需要重新评估冰层消失的可能。这里引出了从贝叶斯角度看概率。

在模式识别领域，我们需要一种更通用的关于概率的表达。1.1节中提到多项式拟合问题，我们当然可以很自然的用训练集的频率来代表随机变量tn(target value)的概率，但是对于估计正确参数w来说，我们更应该用不确定性来理解，从贝叶斯角度来解释概率论中的不确定性，用于模型参数估计以及模型的选择。

假设在观察数据之前，我们有一个关于w的先验p(w)，那么根据w我们观察到数据集D：可以用条件概率来表示p(D|w)，贝叶斯定理可以表达为：

根据上式，我们可以根据给定的观察数据D，来估计w的不确定性，即w的后验概率p(w|D)。其中的条件概率p(D|w)可以表示成关于w的一个function，称之为似然方程（likelihood function）。可以理解为在给定w的情况下，观察到当前D的可能性。注意：似然并不是关于w的概率密度函数。

P(D)是不变的，可以理解为一个归一化常数，因此，我们可以得到正比关系：

后验是关于w的概率密度函数，因此它关于w的积分为1。另外，P(D)可以理解为全概率公式，

一种广泛使用的统计估计方法是最大似然估计，通过最大化似然方程p(D|w)来得到w。意思是说找到一个w，使得观察到当前D的概率最大化。很多情况下，我们用-ln（p(D|w)）来求解最小值，主要是为了方便，并且ln是单调的。

前面提到的贝叶斯方法（1.44），一个很重要的好处是非常自然地引入了先验p(w)，使得我们的估计不会太极端。比如我们对投硬币问题观察到每一次训练数据都是正面，那么最大似然估计得到正面的概率将是1。通过先验的调整我们可以避免这种极端情况。

当然，贝叶斯理论也有它的缺点：有的时候设计者为了计算的方便而选择某个形式的先验，却不是因为相信数据符合这样的先验。如果先验很烂，那么贝叶斯模型的结果往往会很烂。而直接的统计估计方法（如最大似然）可以避免这些问题，并且可以利用例如cross-validation （本章后面有介绍）这样的方法来调参。

1.2.4 高斯分布

高斯分布（正态分布）大概是最重要的关于连续型随机变量的一种概率分布了。关于一个单一的实变量x来说，高斯分布定义为

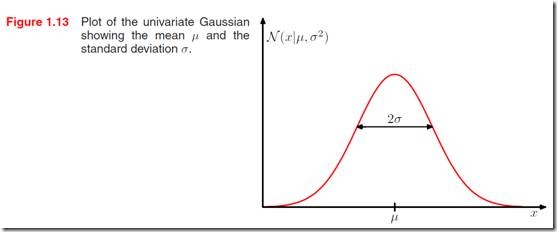
其中，叫做均值mean，叫做方差variance。高斯分布是由这两个参数决定的。另外叫做precision。图1.13绘制了一个典型的高斯分布。

通过下面两个性质：

我们可以知道高斯分布是一个概率密度函数。

通过期望和方差的定义，我们可以求得

这也是叫做均值mean，叫做方差variance的由来。

定义在一个D维度的连续型随机变量（一个向量）x的高斯分布是：

其中均值是D维的，协方差是D*D维的。

假设每一个数据点xi都是独立同分布的，那么基于给定的均值、方差，生成一个数据集x的概率是

也就是似然方程的形式。我们通过最大化似然方程来找到使得生成这样数据集的概率最大的参数。这里有一点绕，理论上我们应该去给定数据集寻找参数的最大概率，这样更自然一些；不过这个目标和最大似然是有联系的，后面会涉及到。基于(1.53)式我们也更容易理解为什么常常需要对似然方程取ln计算，因为取对数之后使得连乘变成了连加，方便计算，同时保证了计算机的精度是有效的。取对数后我们可以得到似然方程：

最大化该式（分别对）可以得到均值和方差的最大似然估计：

可以看到，结果分别是样本均值和样本方差。这样的方法和结果看起来都很简单也有道理，那是不是说以后我们只要计算样本均值和样本方差就行了呢？进一步探究最大似然的结果我们可以发现它有一些不足之处——本质上，它低估了真实方差。我们来求上述解的期望，通过带入期望的定义，不难得到：

可以看到，样本方差的期望不等于真实方差（假设的，未知的），也就是说最大似然的方差估计是有偏估计。这是一种称之为bias的现象（之一），在很多模型中，正是因为最大似然这种bias造成了模型的over-fitting（过拟合）。

1.2.5 曲线拟合问题再思考

让我们继续回到前一节讲的曲线拟合问题中，来逐步揭开更加概率角度的模型理解，用完全贝叶斯角度去做。

我们用不确定性来表达需要求的目标值t（target value）——用概率分布来表达。假设给定一个数据点x，它的目标值t服从一个高斯分布（均值为y(x,w)，方差为），那么：

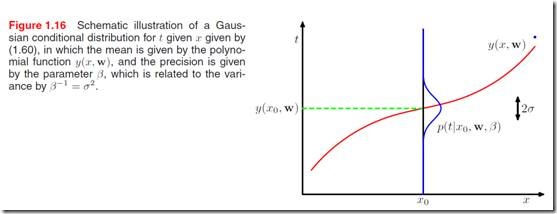
由下图1.16可以看到，红线表示曲线拟合的结果，在每一个点x0上，得到目标值t是在一个范围内变化的。

对（1.60）取对数，得到：

当我们对w求极值的时候，可以看其他参数都是已知的常数，因此最小化（1.62）就等价于最小化 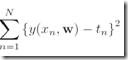这一部分。而这一部分就恰恰是前面我们提到过的error function，称为sum-of-squares。有了w的似然估计以后，我们类似的可以求出precision 的估计值：

好了，当我们有了之后，现在我们可以预测t的概率分布了：

这和我们之前用error function计算最优w再直接得到y作为t的预测不同，现在t是符合一个分布的。

当然，上述结果仍然略显简单，更进一步贝叶斯的方法是引入w的先验。让我们假设w符合下面这样的高斯分布：

其中控制了参数w的分布，像这样的参数称之为超参数。通过贝叶斯定理，可以表达出w的后验概率：

这样我们可以计算w最有可能的取值，在给定数据集（训练集x,t）的情况下。这种方法称为maximum posterior (MAP) 。

用和之前类似的方法，对（1.66）取-ln()，等价于最小化：

这和之前提到的带正则项的error function（regularized sum-of-squares）是一样的。可见，引入了先验在这个例子下面起到了调节过拟合的作用。

1.2.6 贝叶斯曲线拟合

继续思考前面的例子，虽然我们引入了w的先验，但是我们本质上仍然在做w的点估计，即我们得到了一个我们认为最优的w，然后再得到t的估计。事实上，真正贝叶斯的方法因该是对所有w做积分，叫做marginalization，这才是贝叶斯理论的核心所在。应该是这样做的：在给定训练数据集x，t下，我们对所有w的取值求积分

，其中一项是用式子（1.60）来给出的，一项是由前面（1.66）给出的（需要归一化）。通过计算我们可以得到（1.68）左边关于t的分布表达：

上面为了书写清楚，把参数和隐藏了，当做是已知的，后面第三章会讲到怎么求上面的结果，在这里就不具体讲了，有个大概的概念即可。