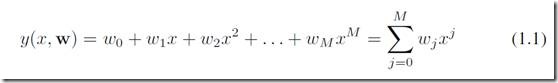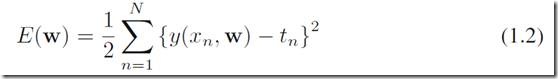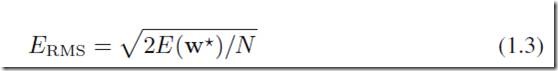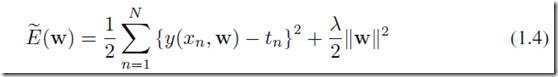今天开始学Pattern Recognition and Machine Learning (PRML)，章节1.1，介绍与多项式曲线拟合(Polynomial Curve Fitting)

转载请注明源地址：http://www.cnblogs.com/xbinworld/archive/2013/04/21/3034300.html 

Pattern Recognition and Machine Learning (PRML)书学习，章节1.1，介绍与多项式曲线拟合(Polynomial Curve Fitting)

博士也快念完了，明年毕业，今年开始准备毕业相关的东西，感觉自己做machine learning 的research做的很散，论文发了些，却不系统。决心在毕业前好好补一下基础知识，我相信离开大学就很难有这样的机会了。以前我入门机器学习是看的《The Elements of Statistic Learning》书，（刚开始半本书看了半年，呵呵，比较累），书很不错。一直听说国外很多学校是用PRML这本书做教材的，自己一直当工具书翻，没有仔细看过，因此就打算看PRML这本书了。

尽量把看的内容写到blog中，我打算前面写的章节可以密集一些，当作基础复习，后面的topic可能会适当精选一些。下面的文字有一些是用原书中的句子翻译来的，但很多是我自己的话，毕竟我不是在翻译；其中的公式和图标，基本上会来自原书，毕竟我写只是blog，全自己写太消耗时间了。

章节1.1多项式曲线拟合(Polynomial Curve Fitting)

很多ML的介绍都是从regression（回归）这个问题开始的，PRML也一样。回归问题是很多现实问题的基本解决方法，比如各类预测问题。不过本书第一张并不涉及具体的算法，不是一上来就说线性回归，而是介绍了很多基础概念，我觉得是本书的一大优点。

给定一个N个样本的训练集合，，对应目标值（观测值）

,我们的目标是在给定训练集合的情况对一个新来的样本,预测他的目标值。事实上，我们是不知道数据本身是否是产生于某种形式的函数方程的，比如正玄函数sin（），而要从观测数据去发现隐含的方程是很困难的。因为数据本身存在了不确定性（uncertainty）。（注：uncertainty的理解将会贯穿本书。）

我们先试图用多项式函数来拟合数据，形式为：

其中y为预测值，x是输入，w是参数。M是多项式的阶（最大次方）。 注意，虽然多项式对x来说是非线性，但是对于所有参数w来说是线性的。线性方程是M=1的情况。这种对w线性的函数称之为线性模型，linear model，将会在第3-4章介绍。

拟合的一种直观做法是去最小化误差函数，error function， 其中一种最常见的error function叫做sum of the squares:

这个式子的特点是非负，只有当所有点都被正确预测时，error为0。式子中的1/2是为了以后推导时候的方便。（对的，你是对的，很多时候是为了求导后把2去掉- -）。

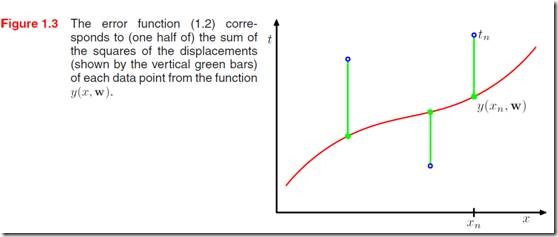
图1.3简单说明了误差函数的值，图中蓝点是训练数据，y是预测模型，绿线的长度之平方和（减半）就是误差函数的值。要估计w的最优值来得到y(x,w)这个函数做预测，我们需要最小化E(W)，因为E(W)是关于w的一个二次方程，是存在全局最优解的，这里可以记最优解的w为。好了，现在剩下的最后一个问题是我们因该怎么确定M，也就是用几阶的多项式来拟合数据呢？

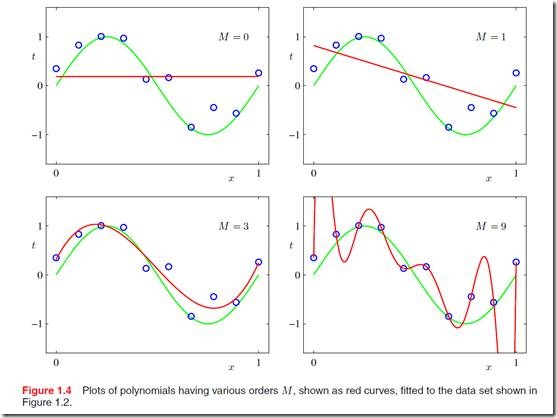
我们来看图1.4， 如果数据本身是通过正玄函数加上一点高斯噪音得到（图中蓝点），当然数据怎么来我们是不知道的。我们用多项式来拟合数据，可以看到，当M从0逐渐增大的时候函数的拟合能力越来越强，也就是说在training set中错误的结果越来越小，当M=9的时候我们发现所有的点都被正确的拟合了。那么是不是我们找到了一个最好的结果呢？其实不然，拟合training set只是我们的手段，我们的目标是得到一个具有很好泛化能力的函数，来预测新的数据点。由图1.4的M=9可以看到，和真实曲线（绿线）相差很远，这里就是一个过拟合的问题（over-fitting），可以说是机器学习里面非常重要的一个问题。

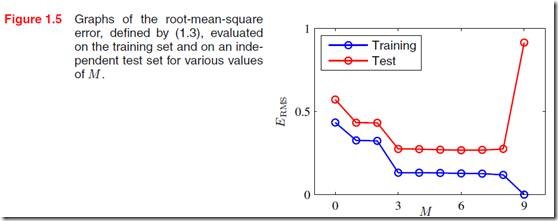
如果记录下均方根误差，root-mean-square error

可以得到图1.5的示例，M到了一定阶段以后在test数据上的error就会显著增大了，我们理解成过拟合了！

我们再来简单讨论一下over-fitting的问题。造成over-fitting的因素很多，我个人理解有两点是很重要的，（1）模型太复杂；（2）数据太少。

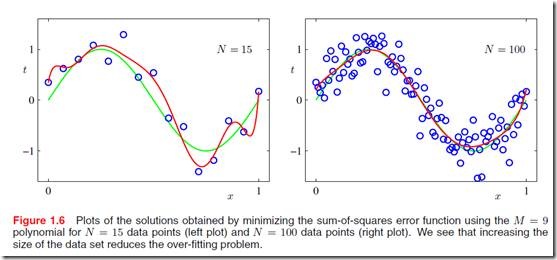
上面的例子说明了，当我们用M=9的时候，模型对于原始数据来说研究太复杂了，但是也可用是因为数据点太少造成过拟合的。看图1.6，当数据点显著增多时，过拟合问题减少了很多！所以，很重要的一点是，训练样本的足够多以及模型的合适。不过训练样本太多也有其他我问题，比如欠拟合，以及训练不动（- -）,这些这里就不谈了。

Machine Learning方法中很重要的一类是正则化，regularization，具体会在以后的章节中仔细介绍。这里给一个直观的理解。最常用的正则化项是约束参数的模，在公式（1.2）对w做约束得到：

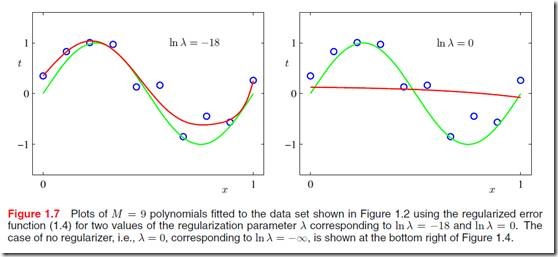
如果y是线性方程的时候，公式（1.4）就是ridge regression了。通过图1.7，我们可以看到改变 的数值可以对模型产生巨大的影响。当依然是用M=9的时候，加入在正则化项就可以比较好的得到拟合了。当然，新问题又来了，怎么确定新引入的参数呢？这又需要一些其他的知识，常见的做法是建立一个validation集合，用来验证参数的选取。后面介绍model selection的时候会讲到一些。

好了，第一小节就介绍到这里，第一章的风格是直观上介绍一些问题，以及给出一些解决方法。对于machine learning 入门的同学是非常好的。