取石子
给出四堆石子,石子数分别为a,b,c,d。规定每次只能从堆顶取走石子,问取走所有石子的方案数。
分析:考虑取出石子的序列长度为a+b+c+d,属于第1堆,第2堆,第3堆,第4堆的分别有a b c d 个
此 答 案 为 C(a+b+c+d,a) C(b+c+d,b) C(c+d,c)=(a+b+c+d)!/(a!b!c!d!)
#include<iostream>
using namespace std;
long long C[2005][2005];
const int mod=1e9+7;
int main()
{
for(int i=0;i<=2000;++i)
{
C[i][0]=1;
for(int j=1;j<=i;++j)
C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
}
int a,b,c,d;
cin>>a>>b>>c>>d;
long long t=C[a+b+c+d][a+b+c]*C[a+b+c][a+b]%mod*C[a+b][a]%mod;
cout<<t<<"\n";
}
AB序列

#include <bits/stdc++.h>
using namespace std;
int n,m,a[200001];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=m;i++)
scanf("%d",&a[i+n]),a[i+n]=-a[i+n];
n=n+m+1;
sort(a+1,a+n+1);
long long sum=0;
for(int i=1;i<=n;i++)
sum+=abs(a[i]-a[(n+1)/2]);
printf("%lld\n",sum);
return 0;
}
小球碰撞
一个弹球(可视为质点)被水平抛出,落地时发生完全弹性碰撞,设弹球第一次落地位置为x,则第i次落地位置为(2i-1)x
若弹球第一次落地的位置在区间[L,R]均匀随机分布,求弹球落在区间[L,R]内的总次数的数学期望值
分析:设第一次落点的位置为x(L<=x<=R) 当x+(k-1)(2x)<=R<x+k(2x) 时碰撞次数为k次
化简得 R/(2k+1)<x<=R/(2k-1)
则期望次数为
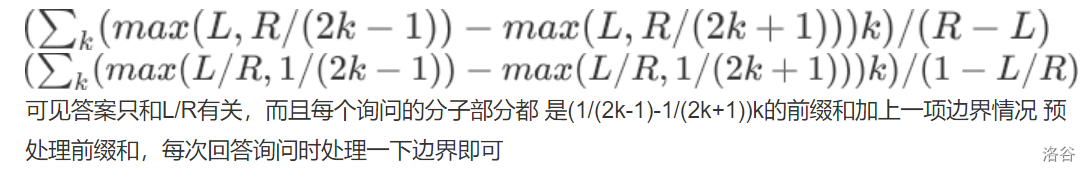
最后一步上下同时除以R就很巧妙!!!
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define P 998244353
int a[20000005],b[20000005],i,l,r,n,t;
int main()
{
for(a[1]=1,i=2;i<10000005;i++)a[i]=(ll)(P-P/i)*a[P%i]%P;
for(i=1;i<10000005;i++)
{
b[i]=b[i-1]+a[i];
if(b[i]>=P)b[i]-=P;
}
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&l,&r);
n=(r+l)/l>>1;
printf("%d\n",(r*(b[n<<1]+(ll)(P-1>>1)*b[n]%P)%P-(ll)l*n%P+P)*a[r-l]%P);
}
return 0;
}
打怪
就是一个简单的dp
设状态为f[i][j][k],表示处理完第i只怪,武器是j,属性是k的最短时间 武器/属性的切换只需在打每只怪之前考虑 转 移的时候,分别考虑武器,属性的转换即
可 由于武器/属性的转换是一个有向图,间接切换可能比直接切换更优, 所以一开始要跑Floyd求最短路。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define P 998244353
ll ans=1LL<<60,f[105][105];
int x[105],y[105],u[105][105],v[105][105],w[105][105][105],s[105],t[105],a,b,n,c,i,j,k,l;
int main()
{
scanf("%d%d%d%d",&a,&b,&c,&n);
for(i=1;i<=a;i++)scanf("%d",x+i);
for(i=1;i<=b;i++)scanf("%d",y+i);
for(i=1;i<=a;i++)for(j=1;j<=a;j++)scanf("%d",u[i]+j);
for(i=1;i<=b;i++)for(j=1;j<=b;j++)scanf("%d",v[i]+j);
for(i=1;i<=c;i++)for(j=1;j<=a;j++)for(k=1;k<=b;k++)scanf("%d",w[i][j]+k);
for(i=1;i<=n;i++)scanf("%d",s+i);
for(i=1;i<=n;i++)scanf("%d",t+i);
for(k=1;k<=a;k++)for(i=1;i<=a;i++)for(j=1;j<=a;j++)u[i][j]=min(u[i][j],u[i][k]+u[k][j]);
for(k=1;k<=b;k++)for(i=1;i<=b;i++)for(j=1;j<=b;j++)v[i][j]=min(v[i][j],v[i][k]+v[k][j]);
for(i=1;i<=a;i++)for(j=1;j<=b;j++)f[i][j]=x[i]+y[j];
for(i=1;i<=n;i++)
{
for(j=1;j<=a;j++)for(k=1;k<=b;k++)for(l=1;l<=a;l++)f[j][k]=min(f[j][k],f[l][k]+u[l][j]);
for(j=1;j<=a;j++)for(k=1;k<=b;k++)for(l=1;l<=b;l++)f[j][k]=min(f[j][k],f[j][l]+v[l][k]);
for(j=1;j<=a;j++)for(k=1;k<=b;k++)f[j][k]+=(s[i]+w[t[i]][j][k]-1)/w[t[i]][j][k];
}
for(i=1;i<=a;i++)for(j=1;j<=b;j++)ans=min(ans,f[i][j]);
cout<<ans<<endl;
return 0;
}