多分类问题:有N个类别C1,C2,...,Cn,多分类学习的基本思路是“拆解法”,即将多分类任务拆分为若干个而分类任务求解,最经典的拆分策略是:“一对一”,“一对多”,“多对多”
(1)一对一
给定数据集D={(x1,y1),(x2,y2),...,(xn,yn)},yi€{c1,c2,...,cN},一对一将这N个类别两两配对,从而产生N(N-1)/2个二分类任务,在测试阶段新样本将同时提交给所有的分类器,于是将得到N(n-1)/2个分类结果,最终把预测最多的结果作为投票结果。
算法:

(2)一对多
一对多则是将每一个样例作为正例,其他剩余的样例作为反例来训练N个分类器,如果在测试时仅有一个分类器产生了正例,则最终的结果为该分类器,如果产生了多个正例,则判断分类器的置信度,选择置信度大的分类别标记作为最终分类结果。
算法:

举例描述:
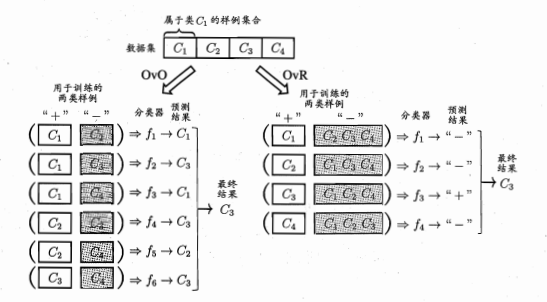
一对一问题:如果有4个类,首先从中任选两个类,进行标记,判断某一个样例更倾向于哪一个类,记录预测的结果,对所有的样例进行判断,看他应该属于两个类中的哪一个,然后选择其他的两个类,重复这个过程,最后收集某一个样例的全部判断结果,会得到不同的结果,找到其中的所占的比例最大的结果即为最终的结果。
(3)多对多问题:
有一种最常用的技术是:”纠错输出码“,分为两个阶段,编码阶段和解码阶段
编码阶段:对N个类别进行M次划分,每次将一部分类划分为正类,一部分类划分为反类,编码矩阵有两种形式:二元码和三元码,前者只有正类和反类,后者除了正类和和反类还有停用类,在解码阶段,各分类器的预测结果联合起来形成测试示例的编码,该编码与各类所对应的编码进行比较,将距离最小的编码所对应的类别作为预测结果。
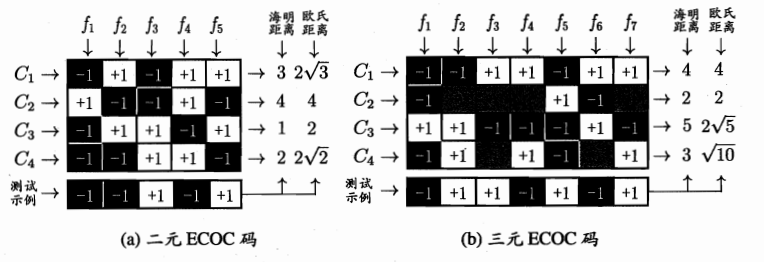
例如:在上图(1)中,f1分类器使得所有的C2为正例,其他为反例,f2分类器使得C1,C3为正,剩余分类器如图所示,因此可以得到一串输入码,以C1为例,其输入码为(-1,+1,-1,+1,+1)对于测试用例(-1,-1,+1,-1,+1)计算它与其他类的距离,即计算输入码和测试用例的欧式距离以C1和测试用例为例=(-1-1)2+(+1-1)2+(-1-1)2+(+1+1)2+(+1-1)2=12½
海明距离: