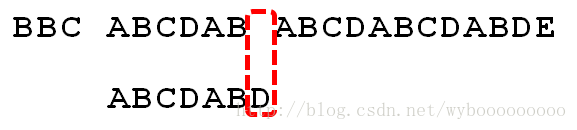字符串匹配-KMP

节选自 https://www.cnblogs.com/zhangtianq/p/5839909.html

字符串匹配 KMP O(m+n）

O原来的暴力算法 当不匹配的时候

尽管之前文本串和模式串已经分别匹配到了S[9]、P[5]，但因为S[10]跟P[6]不匹配，所以文本串回溯到S[5]，模式串回溯到P[0]，从而让S[5]跟P[0]匹配

 而S[5]肯定跟P[0]失配。为什么呢？因为在之前第4步匹配中，我们已经得知S[5] = P[1] = B，而P[0] = A，即P[1] != P[0]，故S[5]必定不等于P[0]，所以回溯过去必然会导致失配。那有没有一种算法，让i 不往回退，只需要移动j 即可呢？

    答案是肯定的。这种算法就是本文的主旨KMP算法，它利用之前已经部分匹配这个有效信息，保持i 不回溯，通过修改j 的位置，让模式串尽量地移动到有效的位置。

 

 

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

• 如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；
• 如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。

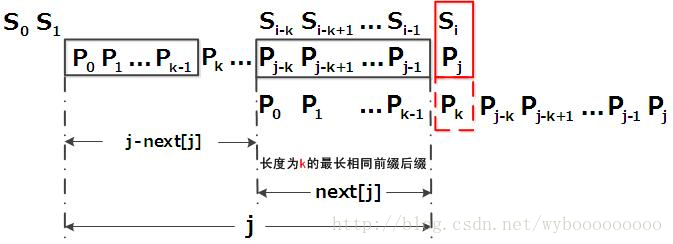
next[j]表示模式串前j-1个字符组成的子串，前缀和后缀相同的最长的长度

 

 

计算next 数组的方法可以采用递推：

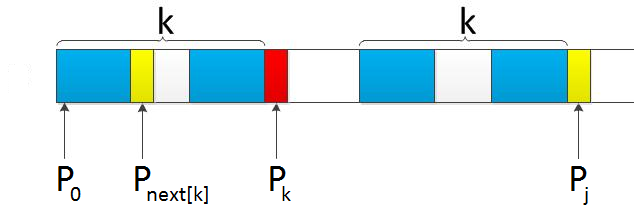
• 1. 如果对于值k，已有p0 p1, ..., pk-1 = pj-k pj-k+1, ..., pj-1，相当于next[j] = k。

• 2.已知next [0, ..., j]，如何求出next [j + 1]呢？

    对于P的前j+1个序列字符：

• 若p[k] == p[j]，则next[j + 1 ] = next [j] + 1 = k + 1；
• 若p[k ] ≠ p[j]，如果此时p[ next[k] ] == p[j ]，则next[ j + 1 ] =  next[k] + 1，否则继续递归前缀索引k = next[k]，而后重复此过程。 相当于在字符p[j+1]之前不存在长度为k+1的前缀"p0 p1, …, pk-1 pk"跟后缀“pj-k pj-k+1, …, pj-1 pj"相等，那么是否可能存在另一个值t+1 < k+1，使得长度更小的前缀 “p0 p1, …, pt-1 pt” 等于长度更小的后缀 “pj-t pj-t+1, …, pj-1 pj” 呢？如果存在，那么这个t+1 便是next[ j+1]的值，此相当于利用已经求得的next 数组（next [0, ..., k, ..., j]）进行P串前缀跟P串后缀的匹配。

那为何递归前缀索引k = next[k]，就能找到长度更短的相同前缀后缀呢？这又归根到next数组的含义。我们拿前缀 p0 pk-1 pk 去跟后缀pj-k pj-1 pj匹配，如果pk 跟pj 失配，下一步就是用p[next[k]] 去跟pj 继续匹配，如果p[ next[k] ]跟pj还是不匹配，则需要寻找长度更短的相同前缀后缀，即下一步用p[ next[ next[k] ] ]去跟pj匹配。此过程相当于模式串的自我匹配，所以不断的递归k = next[k]，直到要么找到长度更短的相同前缀后缀，要么没有长度更短的相同前缀后缀。如下图所示：

    

 

next数组的优化

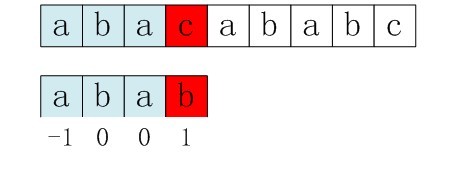
如果用之前的next 数组方法求模式串“abab”的next 数组，可得其next 数组为-1 0 0 1（0 0 1 2整体右移一位，初值赋为-1），当它跟下图中的文本串去匹配的时候，发现b跟c失配，于是模式串右移j - next[j] = 3 - 1 =2位。

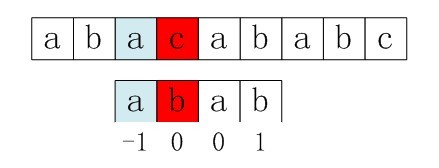
    右移2位后，b又跟c失配。事实上，因为在上一步的匹配中，已经得知p[3] = b，与s[3] = c失配，而右移两位之后，让p[ next[3] ] = p[1] = b 再跟s[3]匹配时，必然失配。问题出在哪呢？

   

    问题出在不该出现p[j] = p[ next[j] ]。为什么呢？理由是：当p[j] != s[i] 时，下次匹配必然是p[ next [j]] 跟s[i]匹配，如果p[j] = p[ next[j] ]，必然导致后一步匹配失败（因为p[j]已经跟s[i]失配，然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配，很显然，必然失配），所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ]咋办呢？如果出现了，则需要再次递归，即令next[j] = next[ next[j] ]。

void GetNextval(char* p, int next[])
{
    int pLen = strlen(p);
    next[0] = -1;
    int k = -1;
    int j = 0;
    while (j < pLen - 1)
    {
        //p[k]表示前缀，p[j]表示后缀
        if (k == -1 || p[j] == p[k])
        {
            ++j;
            ++k;
            //较之前next数组求法，改动在下面4行
            if (p[j] != p[k])
                next[j] = k;   //之前只有这一行
            else
                //因为不能出现p[j] = p[ next[j ]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]
                next[j] = next[k];
        }
        else
        {
            k = next[k];
        }
    }
}

int KmpSearch(char* s, char* p)
{
    int i = 0;
    int j = 0;
    int sLen = strlen(s);
    int pLen = strlen(p);
    while (i < sLen && j < pLen)
    {
        //①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++
        if (j == -1 || s[i] == p[j])
        {
            i++;
            j++;
        }
        else
        {
            //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]
            //next[j]即为j所对应的next值
            j = next[j];
        }
    }
    if (j == pLen)
        return i - j;
    else
        return -1;
}