Description
“我们最新的研究成果《毒药研究方案》被可恶的辛迪加偷走了!”作为拉文霍德的一员,你一定感到很震惊,因为它是我们最尖端的科研人员的一年的研究成果。被辛迪加获得,我们可能会有灭顶之灾。
狡猾的辛迪加为了躲避我们的追杀,他们并没有把《毒药研究方 案》带回激流堡,而是把它藏了起来。但是终究是我们技高一筹,运用侏儒的最新研究成果“静电放射探测器”,我们已经发现了他们的藏身之地。原来他们早就在 奥特兰克山脉的地下修建了一个巨大的城市,现在,他们就把《毒药研究方案》放在了城市的最深处。更好的消息是,我们已经发现了地下城的入口。
作为一名出色的盗贼,你要学会以彼之道,还施彼身——把《毒药研究方案》偷回来。然而辛迪加布置了严密的防御,更糟糕的是,他们从地精购买了电磁监视器。无论你的潜行技巧有多么高明,只要一接近它,就会出发警报。只有破坏它的供电系统,才能电磁监视器悄无声息得失效。
现在,“静电放射探测器”已经为我们生成了一张地图,它可以告诉你整个地下城的布局结构,包括每一个电磁监视器的位置,及其供电装置的位置。辛迪加的地下城可以被描述为一个N*N的表格,城市的入口在(1,1)处,目标《毒药研究方案》在(N,N)处。每个单元格可能是一片空地、一个障碍物、一个辛迪加卫士、一个电磁监视器、或者一个的供电装置。
从入口处开始,每步你只能上、下、左、右移动到相邻的一个单元 格,不可以停留在原地。你只能进入空地,或者失去供电系统的电磁监视器的位置,或者摧毁供电装置。你不能移动到障碍物上,也不能进入辛迪加卫士的视线中。 辛迪加卫士可以监视自己所在单元格以及上下左右共五格的位置,而且他们的视线可以重叠。你不能杀死辛迪加卫士,也不能被他们发现。每个电磁监视器的供电装 置可能存在,也可能无法破坏或者根本不存在。一个供电装置也可能会对应零个、一个或多个电磁监视器,意味着摧毁它,对应的所有电磁监视器都会失效。(1,1)和(N,N)一定是可以通行的。
拉文霍德要求你在执行任务之前首先给出一个计划书,即要求算出至少一共需要多少步,才能拿到我们的《毒药研究方案》。
Input
第1行,两个整数N, M。表示地图大小为N * N,供电装置的数量为M。
第2-N+1行,每行N个整数,每个整数i可能是0,-1,-2或者一个正整数。i=0表示该位置为一块空地,i=-1表示该位置为一个障碍物,i=-2表示该位置为一个辛迪加卫士。如果i是一个属于[1,M]的正整数,则表示该位置为一个供电装置,其编号为i。如果i是一个大于M的正整数,则表示该位置为一个电磁监视器,它的电力由编号为i-M的供电装置提供。
Output
一个整数,为拿到《毒药研究方案》所需的最少的步数。如果不能到达输出-1.
Sample Input
6 2
0 0 0 -2 -1 2
-1 0 0 0 -1 0
-2 0 0 0 3 3
-2 0 0 -1 -1 4
0 -1 0 0 -1 0
1 0 0 0 -1 0
Sample Output
24
Hint
样例说明
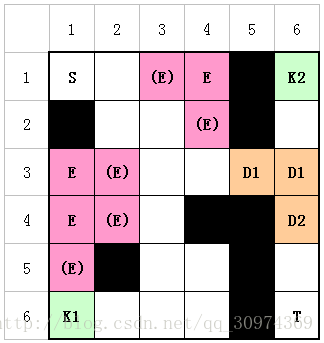
地图如下图,S为入口,T为目标,黑色的单元格为障碍物。每个E表示一个卫兵,(E)为卫兵的监视范围。K1表示供电装置1,K2表示供电装置2。D1表示供电装置为1的电磁监视器,D2表示供电装置为2的电磁监视器。
最优的路线为(1,1) →(1,2) →(2,2) →(2,3) →(3,3) →(4,3) →(5,3) →(6,3) →(6,2) →(6,1)(破坏供电1) →(6,2) →(6,3) →(5,3) →(4,3) →(3,3) →(3,4) →(3,5) →(3,6) →(2,6) →(1,6)(破坏供电2) →(2,6) →(3,6) →(4.6) →(5,6) →(6,6)
数据规模
这道题目的空间限制是512MB
对于15%数据
M=0
对于40%数据
M<=2
对于100%数据
2<=N<=50
0<=M<=16
思路
- m<=16,状压bfs
- ttt为状态,num为方案数
- 一直提交不过后来发现问题在输入,-1会覆盖-2
代码
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
int n,m,a[53][53],fx[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
bool vis[53][53][65555];
struct node{int x,y,num,tt;};
queue<node> q;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j) scanf("%d",&a[i][j]);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j) if(a[i][j]==-2)
for(int k=0;k<4;++k)
if(a[i+fx[k][0]][j+fx[k][1]]!=-2) a[i+fx[k][0]][j+fx[k][1]]=-1;
if(a[1][1]==-1||a[n][n]==-1){puts("-1"); return 0;}
q.push((node){1,1,0,0}); vis[1][1][0]=1;
while(!q.empty())
{
node now=q.front(); q.pop();
for(int i=0;i<4;++i)
{
int x=now.x+fx[i][0],y=now.y+fx[i][1];
if(vis[x][y][now.tt]||x<1||x>n||y<1||y>n||a[x][y]==-1||a[x][y]==-2) continue;
vis[x][y][now.tt]=1;
if(a[x][y]>m){
if(now.tt&(1<<a[x][y]-1-m))
q.push((node){x,y,now.num+1,now.tt});
}
else if(!a[x][y]) q.push((node){x,y,now.num+1,now.tt});
else
{
if(!(now.tt&(1<<a[x][y]-1)))
{
int ttt=now.tt|(1<<a[x][y]-1);
vis[x][y][ttt]=1;
q.push((node){x,y,now.num+1,ttt});
}
}
if(x==n&&y==n) {cout<<now.num+1<<'
'; return 0;}
}
}
puts("-1");
return 0;
}