以前我们学习了线段树可以知道,线段树的每一个节点都储存的是一段区间,所以线段树可以做简单的区间查询,更改等简单的操作。
而后面再做有些题目,就可能会碰到一种回退的操作。这里的回退是指回到未做各种操作之前的状态。
回退的时候,如果暴力点,就直接将每步所操作的线段树都存下来,然后直接翻阅回去,这种方法虽然简单,但是对空间和时间的需求太大了,肯定不能过。
所以这时候我们就可以选择可持久化操作。
可持久化是数据结构里面的一种方法,其总体就是把一个数据结构的历史状态全部都保存下来,从而能够快速的查找之前出现过的某个操作的结果,并且还可以对其继续操作。但是与直接暴力不一样,做修改的时候,每一次修改,只有一条链上的节点被修改,而其他的节点信息都没有变。因此,我们就可以只对这一次的修改操作新建包括一个新根在内的logn个节点,其他的节点我们与上一课树共用。这样一来,我们既能保存之前的信息,又能进行修改操作。
而一般常用的数据结构里面用到的可持久化的线段树。
可持久化的线段树,又叫主席树。其思想大概就如图。在每一步的线段树操作后将改变的那一条链给单独拎出来,然后新建一次链,而没有改变的链就不动,再将新链与不动的那部分重新组合一下,就成了。
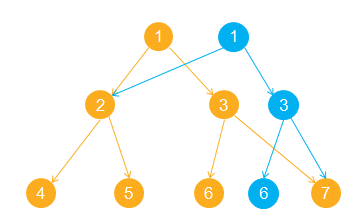
直接看模板裸题吧 https://www.luogu.org/problemnew/show/P3919
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
typedef unsigned long long int ull;
const int inf = 0x3f3f3f3f;
int dir[8][2]={{1,0},{0,1},{1,1},{1,-1},{-1,1},{-1,-1},{0,-1},{-1,0}};
#define pi acos(-1)
#define ls rt<<1
#define rs rt<<1|1
#define me0(s) memset(s,0,sizeof(s))
#define me1(s) memset(s,1,sizeof(s))
#define mef(s) memset(s,-1,sizeof(s))
#define meinf(s) memset(s,inf,sizeof(s))
const int N=1e5+5;
struct node{
int lc,rc;
ll v;
}tr[N<<8];
int root[N<<5]; // root[i]表示版本号为i的线段树的根节点编号
ll a[N];
int n,m,tot;
int build(int l,int r){
int pos=++tot;
if(l==r){
tr[pos].v=a[l];
}
else{
int m=(l+r)>>1;
tr[pos].lc=build(l,m);
tr[pos].rc=build(m+1,r);
}
return pos;
}
int query(int pos,int p,int l,int r){ //查询版本pos中a[p]的值
if(l==r){
return tr[pos].v;
}
int m=(l+r)>>1;
if(p<=m) return query(tr[pos].lc,p,l,m);
else return query(tr[pos].rc,p,m+1,r);
}
int update(int old,int p,int c,int l,int r){
//在old版本上修改a[p]为c
int pos=++tot;
if(l==r){
tr[pos].v=c;
return pos;
}
tr[pos].lc=tr[old].lc;
tr[pos].rc=tr[old].rc; //复制以前的树
int m=(l+r)>>1;
if(p<=m) tr[pos].lc=update(tr[old].lc,p,c,l,m);
else tr[pos].rc=update(tr[old].rc,p,c,m+1,r);
return pos;
}
int main(int argc, char * argv[])
{
std::ios::sync_with_stdio(false);
while(cin>>n>>m){
tot=0;
for(int i=1;i<=n;i++) cin>>a[i];
root[0]=build(1,n);
int v,x,l,w;
for(int i=1;i<=m;i++){
cin>>v>>x>>l;
if(x==1){
cin>>w;
root[i]=update(root[v],l,w,1,n);
}
else{
root[i]=root[v];
cout<<query(root[v],l,1,n)<<endl;
}
}
}
return 0;
}
然后是用主席树求区间第k大/小的板子题目
https://www.luogu.org/problemnew/show/P3834
//区间第k小
#include<bits/stdc++.h>
#define ll long long int
using namespace std;
const int maxn=1e5+6;
ll cnt,n,m,x,y,k,a[maxn];
int root[maxn];
struct node{
int l,r,sum;
}tr[maxn*40];
vector<int> v;
void init(){
cnt=0;
tr[cnt].l=0;
tr[cnt].r=0;
tr[cnt].sum=0;
root[cnt]=0;
v.clear();
}
ll getid(ll x){
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void update(int l,int r,int &x,int y,int pos){
tr[++cnt]=tr[y];
tr[cnt].sum++;
x=cnt;
if(l==r) return ;
int m=(l+r)>>1;
if(pos<=m) update(l,m,tr[x].l,tr[y].l,pos);
else update(m+1,r,tr[x].r,tr[y].r,pos);
}
ll query(ll l,ll r,ll x,ll y,ll k){
if(l==r) return l;
ll m=(l+r)>>1;
ll sum=tr[tr[y].l].sum-tr[tr[x].l].sum;
if(sum>=k) return query(l,m,tr[x].l,tr[y].l,k);
else return query(m+1,r,tr[x].r,tr[y].r,k-sum);
}
int main(){
cin>>n>>m;
init();
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
v.push_back(a[i]);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
for(int i=1;i<=n;i++)
update(1,n,root[i],root[i-1],getid(a[i]));
while(m--){
int l,r,k;
cin>>l>>r>>k;
cout<<v[query(1,n,root[l-1],root[r],k)-1]<<endl;
}
return 0;
}
还有一题杭电多校赛第二场的:http://acm.hdu.edu.cn/showproblem.php?pid=6601
给定数组a,求所给定的区间的内能构成的最大的三角形的周长。
首先想到的是数组内排序,然后一个一个遍历,那么复杂度就达到了O(mnlogn),肯定超时了。
然后赛后补题,用主席树求出区间的第k小的值,然后代替排序。
//区间第k小
#include<bits/stdc++.h>
#define ll long long int
using namespace std;
const int maxn=1e5+6;
ll cnt,n,m,x,y,k,a[maxn];
int root[maxn];
struct node{
int l,r,sum;
}tr[maxn*40];
vector<int> v;
void init(){
cnt=0;
tr[cnt].l=0;
tr[cnt].r=0;
tr[cnt].sum=0;
root[cnt]=0;
v.clear();
}
ll getid(ll x){
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void update(int l,int r,int &x,int y,int pos){
tr[++cnt]=tr[y];
tr[cnt].sum++;
x=cnt;
if(l==r) return ;
int m=(l+r)>>1;
if(pos<=m) update(l,m,tr[x].l,tr[y].l,pos);
else update(m+1,r,tr[x].r,tr[y].r,pos);
}
ll query(ll l,ll r,ll x,ll y,ll k){
if(l==r) return l;
ll m=(l+r)>>1;
ll sum=tr[tr[y].l].sum-tr[tr[x].l].sum;
if(sum>=k) return query(l,m,tr[x].l,tr[y].l,k);
else return query(m+1,r,tr[x].r,tr[y].r,k-sum);
}
int main(){
while(~scanf("%lld%lld",&n,&m)){
init();
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
v.push_back(a[i]);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
for(int i=1;i<=n;i++)
update(1,n,root[i],root[i-1],getid(a[i]));
while(m--){
int l,r;
scanf("%d%d",&l,&r);
ll l1=0,l2=0,l3=0;
ll ans=-1;
if(r-l+1<3)printf("-1
");
else{
for(int k=(r-l+1);k>0;k--){
int x=v[query(1,n,root[l-1],root[r],k)-1];
if(l1==0) l1=x;
else if(l2==0) l2=x;
else if(l3==0) l3=x;
else{
l1=l2;
l2=l3;
l3=x;
}
if(l3+l2>l1) {
ans=1ll*l1+l2+l3;
break;
}
}
printf("%lld
",ans);
}
}
}
return 0;
}