Pig is visiting a friend.
Pig's house is located at point 0, and his friend's house is located at point m on an axis.
Pig can use teleports to move along the axis.
To use a teleport, Pig should come to a certain point (where the teleport is located) and choose where to move: for each teleport there is the rightmost point it can move Pig to, this point is known as the limit of the teleport.
Formally, a teleport located at point x with limit y can move Pig from point x to any point within the segment [x; y], including the bounds.
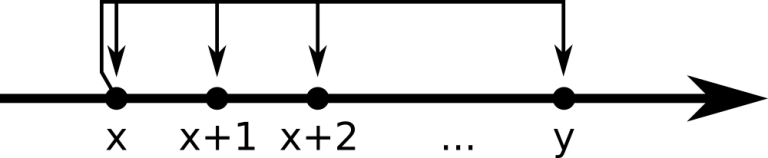
Determine if Pig can visit the friend using teleports only, or he should use his car.
The first line contains two integers n and m (1 ≤ n ≤ 100, 1 ≤ m ≤ 100) — the number of teleports and the location of the friend's house.
The next n lines contain information about teleports.
The i-th of these lines contains two integers ai and bi (0 ≤ ai ≤ bi ≤ m), where ai is the location of the i-th teleport, and bi is its limit.
It is guaranteed that ai ≥ ai - 1 for every i (2 ≤ i ≤ n).
Print "YES" if there is a path from Pig's house to his friend's house that uses only teleports, and "NO" otherwise.
You can print each letter in arbitrary case (upper or lower).
3 5
0 2
2 4
3 5
YES
3 7
0 4
2 5
6 7
NO
The first example is shown on the picture below:
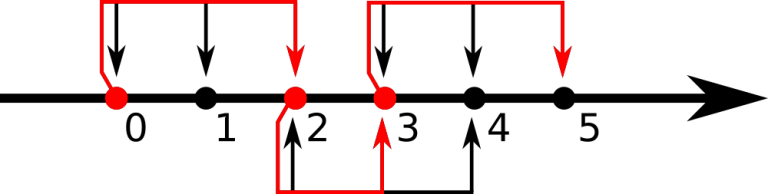
Pig can use the first teleport from his house (point 0) to reach point 2, then using the second teleport go from point 2 to point 3, then using the third teleport go from point 3 to point 5, where his friend lives.
The second example is shown on the picture below:
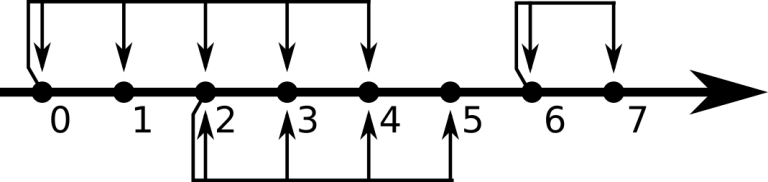
You can see that there is no path from Pig's house to his friend's house that uses only teleports.
题意：pig要从0到m，他只能乘坐这个teleport过去，每次teleport能从ai出发到[ai,bi]中的任意一个位置。请问pig能只乘坐teleport到达m吗？
题解：就是看0~m上是否有没有被线段覆盖过的部分，经典做法for一遍就好了。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=1e3+10; 9 int a[N]; 10 bool flag; 11 int main() 12 { 13 int n,m,l,r; 14 scanf("%d%d",&n,&m); 15 for(int i=1;i<=n;i++) 16 { 17 scanf("%d%d",&l,&r); 18 a[2*l]++; 19 a[2*r+1]--; 20 } 21 flag=0; 22 int ans=0; 23 for(int i=0;i<=2*m;i++) 24 { 25 ans+=a[i]; 26 if(ans==0) 27 flag=1; 28 } 29 if(flag) 30 printf("NO "); 31 else 32 printf("YES "); 33 return 0; 34 }
You are given a rooted tree with n vertices. The vertices are numbered from 1 to n, the root is the vertex number 1.
Each vertex has a color, let's denote the color of vertex v by cv. Initially cv = 0.
You have to color the tree into the given colors using the smallest possible number of steps. On each step you can choose a vertex v and a color x, and then color all vectices in the subtree of v (including v itself) in color x. In other words, for every vertex u, such that the path from root to u passes through v, set cu = x.
It is guaranteed that you have to color each vertex in a color different from 0.
You can learn what a rooted tree is using the link: https://en.wikipedia.org/wiki/Tree_(graph_theory).
The first line contains a single integer n (2 ≤ n ≤ 104) — the number of vertices in the tree.
The second line contains n - 1 integers p2, p3, ..., pn (1 ≤ pi < i), where pi means that there is an edge between vertices i and pi.
The third line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ n), where ci is the color you should color the i-th vertex into.
It is guaranteed that the given graph is a tree.
Print a single integer — the minimum number of steps you have to perform to color the tree into given colors.
6
1 2 2 1 5
2 1 1 1 1 1
3
7
1 1 2 3 1 4
3 3 1 1 1 2 3
5
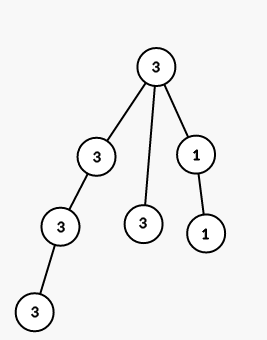
The tree from the first sample is shown on the picture (numbers are vetices' indices):
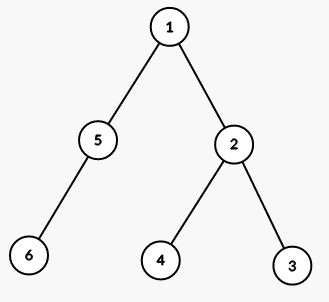
On first step we color all vertices in the subtree of vertex 1 into color 2 (numbers are colors):
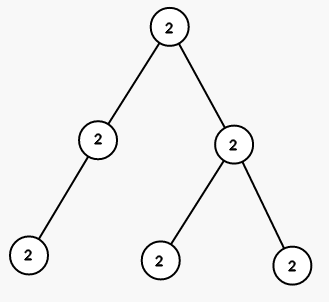
On seond step we color all vertices in the subtree of vertex 5 into color 1:
On third step we color all vertices in the subtree of vertex 2 into color 1:
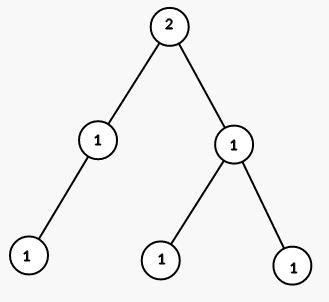
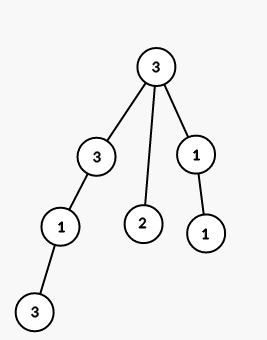
The tree from the second sample is shown on the picture (numbers are vetices' indices):
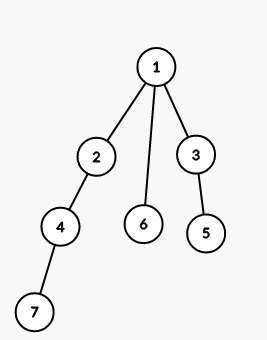
On first step we color all vertices in the subtree of vertex 1 into color 3 (numbers are colors):
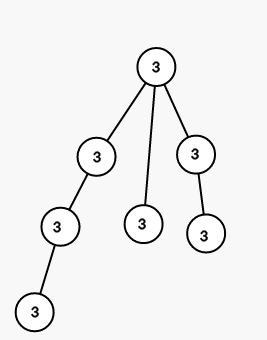
On second step we color all vertices in the subtree of vertex 3 into color 1:
On third step we color all vertices in the subtree of vertex 6 into color 2:
On fourth step we color all vertices in the subtree of vertex 4 into color 1:
On fith step we color all vertices in the subtree of vertex 7 into color 3:
题意：给你一颗树，初始无色，为颜色0。然后输入指定树上每个结点的颜色。你每次染色必须选定一个结点，把该结点的子树全染成同一颜色。问你至少需要多少次染色才能把整颗树染成指定的颜色。
题解：写个dfs，如果当前结点u和子结点p的颜色不同，那么u的子树的染色数+=p的子树的染色数，否则u的子树的染色数+=p的子树的染色数-1。初始每个结点染色数为1。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=1e5+10; 9 struct edg 10 { 11 int next,to; 12 }edge[N*2]; 13 int head[N],ecnt; 14 void addedge(int u,int v) 15 { 16 edge[++ecnt]=(edg){head[u],v}; 17 head[u]=ecnt; 18 return ; 19 } 20 int col[N],num[N]; 21 int n,m,k,t; 22 void dfs(int u,int pre) 23 { 24 int p; 25 num[u]=1; 26 for(int i=head[u];i!=-1;i=edge[i].next) 27 { 28 p=edge[i].to; 29 if(p!=pre) 30 { 31 dfs(p,u); 32 if(col[u]==col[p]) 33 num[u]+=num[p]-1; 34 else 35 num[u]+=num[p]; 36 } 37 } 38 return ; 39 } 40 int main() 41 { 42 scanf("%d",&n); 43 ecnt=0; 44 clr_1(head); 45 for(int i=2;i<=n;i++) 46 { 47 scanf("%d",&k); 48 addedge(k,i); 49 addedge(i,k); 50 } 51 for(int i=1;i<=n;i++) 52 scanf("%d",col+i); 53 dfs(1,1); 54 printf("%d ",num[1]); 55 return 0; 56 }
Sasha is taking part in a programming competition. In one of the problems she should check if some rooted trees are isomorphic or not. She has never seen this problem before, but, being an experienced participant, she guessed that she should match trees to some sequences and then compare these sequences instead of trees. Sasha wants to match each tree with a sequence a0, a1, ..., ah, where h is the height of the tree, and ai equals to the number of vertices that are at distance of i edges from root.
Unfortunately, this time Sasha's intuition was wrong, and there could be several trees matching the same sequence. To show it, you need to write a program that, given the sequence ai, builds two non-isomorphic rooted trees that match that sequence, or determines that there is only one such tree.
Two rooted trees are isomorphic, if you can reenumerate the vertices of the first one in such a way, that the index of the root becomes equal the index of the root of the second tree, and these two trees become equal.
The height of a rooted tree is the maximum number of edges on a path from the root to any other vertex.
The first line contains a single integer h (2 ≤ h ≤ 105) — the height of the tree.
The second line contains h + 1 integers — the sequence a0, a1, ..., ah (1 ≤ ai ≤ 2·105). The sum of all ai does not exceed 2·105. It is guaranteed that there is at least one tree matching this sequence.
If there is only one tree matching this sequence, print "perfect".
Otherwise print "ambiguous" in the first line. In the second and in the third line print descriptions of two trees in the following format: in one line print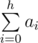 
integers, the k-th of them should be the parent of vertex k or be equal to zero, if the k-th vertex is the root.
These treese should be non-isomorphic and should match the given sequence.
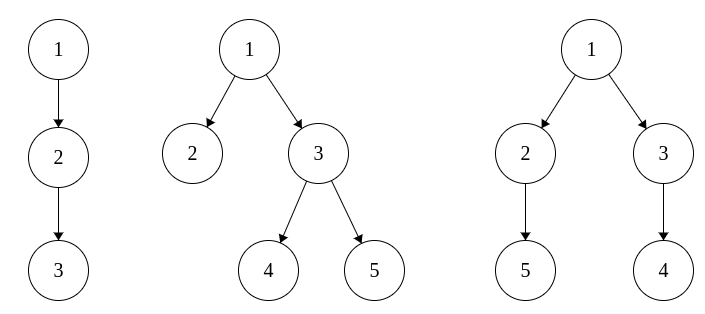
2
1 1 1
perfect
2
1 2 2
ambiguous
0 1 1 3 3
0 1 1 3 2
The only tree in the first example and the two printed trees from the second example are shown on the picture:
题意：给你一串序列a0~ah，ai代表深度为i的结点的个数，问你能不能构造出两棵符合序列的不同构的树，如果能，输出ambiguous以及描述任意两棵不同构并且符合序列的树。不能则输出perfect。
题解：很显然，只要ai≥ 2并且 ai-1 ≥2，那么这个序列就能造出不同构的两棵树，否则该序列只能表示唯一的一棵树。
那么怎么构造这棵树呢。我们做个ai前缀和prei代表该层最后一个结点的编号。那么我们第一棵树把所有同层结点连接在上一层最后一个结点上就行了。第二棵树找到第一个ai≥ 2并且 ai-1 ≥2的i层，一个点链到上层的倒数第二个结点，其他都链到最后一个结点。对于其余层和第一棵树的做法一样。这样就能构造出不同构的两棵树了。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=2e5+10; 9 int a[N],pre[N]; 10 int fa[N]; 11 bool flag; 12 int n,m,k; 13 int main() 14 { 15 scanf("%d",&n); 16 a[0]=pre[0]=0; 17 for(int i=1;i<=n+1;i++) 18 { 19 scanf("%d",a+i); 20 if(a[i-1]>=2 && a[i]>=2) 21 flag=1; 22 pre[i]=pre[i-1]+a[i]; 23 } 24 if(!flag) 25 { 26 printf("perfect "); 27 } 28 else 29 { 30 printf("ambiguous "); 31 for(int i=1;i<=n+1;i++) 32 for(int j=1;j<=a[i];j++) 33 printf(" %d",pre[i-1]); 34 printf(" "); 35 flag=1; 36 for(int i=1;i<=n+1;i++) 37 if(flag && a[i-1]>=2 && a[i]>=2) 38 { 39 for(int j=1;j<=a[i]-1;j++) 40 printf(" %d",pre[i-1]); 41 printf(" %d",pre[i-1]-1); 42 flag=0; 43 } 44 else 45 { 46 for(int j=1;j<=a[i];j++) 47 printf(" %d",pre[i-1]); 48 } 49 printf(" "); 50 } 51 return 0; 52 }
Suppose you have two polynomials 
and 
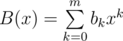. Then polynomial 
can be uniquely represented in the following way:
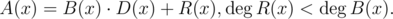
This can be done using long division. Here,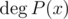 
denotes the degree of polynomial P(x). 
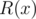is called the remainder of division of polynomial by polynomial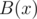 
, it is also denoted as 
.
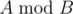Since there is a way to divide polynomials with remainder, we can define Euclid's algorithm of finding the greatest common divisor of two polynomials. The algorithm takes two polynomials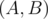 
. If the polynomial 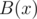is zero, the result is , otherwise the result is the value the algorithm returns for pair 
. On each step the degree of the second argument decreases, so the algorithm works in finite number of steps. But how large that number could be? You are to answer this question.
You are given an integer n. You have to build two polynomials with degrees not greater than n, such that their coefficients are integers not exceeding 1 by their absolute value, the leading coefficients (ones with the greatest power of x) are equal to one, and the described Euclid's algorithm performs exactly n steps finding their greatest common divisor. Moreover, the degree of the first polynomial should be greater than the degree of the second. By a step of the algorithm we mean the transition from pair 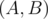to pair .
You are given a single integer n (1 ≤ n ≤ 150) — the number of steps of the algorithm you need to reach.
Print two polynomials in the following format.
In the first line print a single integer m (0 ≤ m ≤ n) — the degree of the polynomial.
In the second line print m + 1 integers between - 1 and 1 — the coefficients of the polynomial, from constant to leading.
The degree of the first polynomial should be greater than the degree of the second polynomial, the leading coefficients should be equal to 1. Euclid's algorithm should perform exactly n steps when called using these polynomials.
If there is no answer for the given n, print -1.
If there are multiple answer, print any of them.
1
1
0 1
0
1
2
2
-1 0 1
1
0 1
In the second example you can print polynomials x2 - 1 and x. The sequence of transitions is
There are two steps in it.
题意:给定多项式的最高次数，类似于高精度除法，做多项式除法（具体公式题目中表示出来了），然后有了多项式除法延伸出多项式gcd的欧几里得算法。让你构造两个最高次数小于等于n的多项式，并且其中一个最高次数要等于n，并且他们能做n步的欧几里得算法。
题解:一个玄学构造题，我们设定p0=1，p1=x,那么pn=pn-1*x±pn-2，加和减具体看加减上去以后会不会出现除-1,0,1以外的数。同样的还可以构造pn=pn-1*x+pn-2mod 2，
超过1的系数mod 2
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define LL long long 5 #define mod 1000000007 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=2e5+10; 9 int a[1000],acnt; 10 int b[1000],bcnt; 11 int c[1000],ccnt; 12 void dfs(int k) 13 { 14 if(k==0) 15 { 16 a[0]=1; 17 acnt=1; 18 bcnt=0; 19 return ; 20 } 21 dfs(k-1); 22 ccnt=acnt; 23 for(int i=0;i<acnt;i++) 24 c[i]=a[i]; 25 for(int i=acnt;i>0;i--) 26 a[i]=a[i-1]; 27 a[0]=0; 28 acnt++; 29 int flag=1; 30 for(int i=0;i<bcnt;i++) 31 if(a[i]+b[i]>1 || a[i]+b[i]<-1) 32 { 33 flag=-1; 34 break; 35 } 36 for(int i=0;i<acnt;i++) 37 if(i<bcnt) 38 a[i]+=flag*b[i]; 39 for(int i=0;i<ccnt;i++) 40 b[i]=c[i]; 41 bcnt=ccnt; 42 return ; 43 } 44 int main() 45 { 46 int n; 47 scanf("%d",&n); 48 dfs(n); 49 printf("%d ",acnt-1); 50 for(int i=0;i<acnt;i++) 51 printf("%d ",a[i]); 52 printf(" "); 53 printf("%d ",bcnt-1); 54 for(int i=0;i<bcnt;i++) 55 printf("%d ",b[i]); 56 printf(" "); 57 return 0; 58 }