八皇后8皇后，探讨最效率的算法。

数据结构与算法之美|极客时间，里边的课程，关于八皇后的问题。我喜欢先说结果，然后带着疑问去学习。结果：我感觉我的效率比老师的快百分之50，也许老师的只是想让我们易读懂。

哪位大神觉得自己效率高的贴在留言区，我们要互相学习，才能进步~

结果截图：

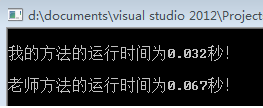
老师的代码如下：

int nTotal2 = 0;
int result2[8] = {0};
bool isOk(int row, int column) {//判断row行column列放置是否合适
	int leftup = column - 1, rightup = column + 1;
	for (int i = row-1; i >= 0; --i) { // 逐行往上考察每一行
		if (result2[i] == column) return false; // 第i行的column列有棋子吗？
		if (leftup >= 0) { // 考察左上对角线：第i行leftup列有棋子吗？
			if (result2[i] == leftup) return false;
		}
		if (rightup < 8) { // 考察右上对角线：第i行rightup列有棋子吗？
			if (result2[i] == rightup) return false;
		}
		--leftup; ++rightup;
	}
	return true;
}
void cal8queens(int row) {
	if (row == 8) { // 8个棋子都放置好了，打印结果
		++nTotal2;
		return; // 8行棋子都放好了，已经没法再往下递归了，所以就return
	}
	for (int column = 0; column < 8; ++column) { // 每一行都有8中放法
		if (isOk(row, column)) { // 有些放法不满足要求
			result2[row] = column; // 第row行的棋子放到了column列
			cal8queens(row+1); // 考察下一行
		}
	}
}

我的代码：

const int MaxLen = 8;
int nTotal1 = 0;
int result1[8] = {0};
void EnterNextLayer(int nNextX)
{
	if (nNextX == MaxLen)
	{
		++nTotal1;
		return;
	}
	//开始判断nNextX层
	bool bEnterNext = true;
	for (int nLegalY = 0; nLegalY < MaxLen; ++nLegalY)
	{
		bEnterNext = true;
		for (int i = 0; i < nNextX; ++i)
		{
			if(i == nNextX
				|| result1[i] == nLegalY
				|| (i - result1[i]) == (nNextX - nLegalY)
				|| (i + result1[i]) == (nNextX + nLegalY))
			{
				bEnterNext = false;
				break;
			}
		}
		if (bEnterNext)
		{
			result1[nNextX] = nLegalY;
			EnterNextLayer(nNextX + 1);
		}
	}
}

　　

测试效率代码:

#include <iostream>
#include <time.h>
#include <math.h>
int main()
{
	clock_t start,finish;
	start=clock();
	for (int i = 0;i<100;++i)
	{
		nTotal1 = 0;
		EnterNextLayer(0);
		//std::cout<<nTotal1<<std::endl;
	}
	finish=clock();
	std::cout<<"
方法1的运行时间为"<<(double)(finish-start)/CLOCKS_PER_SEC<<"秒！"<<std::endl;

	start=clock();
	for (int i = 0;i<100;++i)
	{
		nTotal2 = 0;
		cal8queens(0);
	}
	finish=clock();
	std::cout<<"
方法2的运行时间为"<<(double)(finish-start)/CLOCKS_PER_SEC<<"秒！"<<std::endl;

	return 0;
}