题目链接
思路:以中序遍历为例,在
现在将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
如何标记呢,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
如下所示是带有标记的迭代中序遍历:
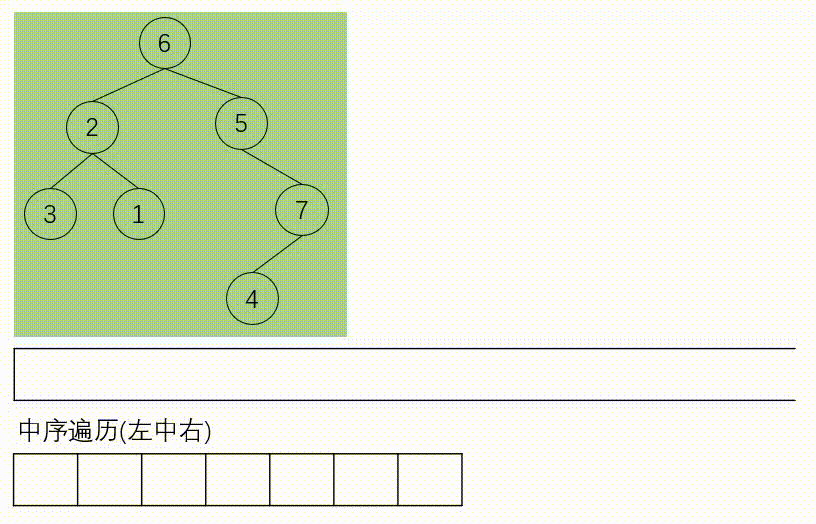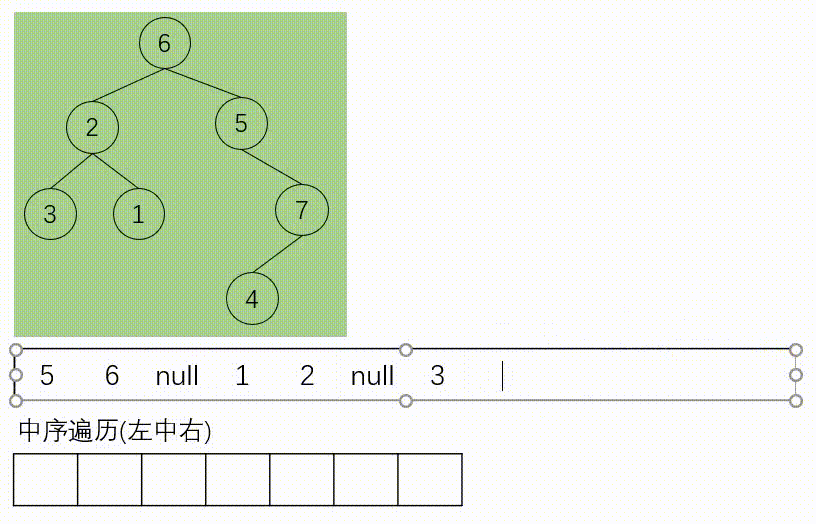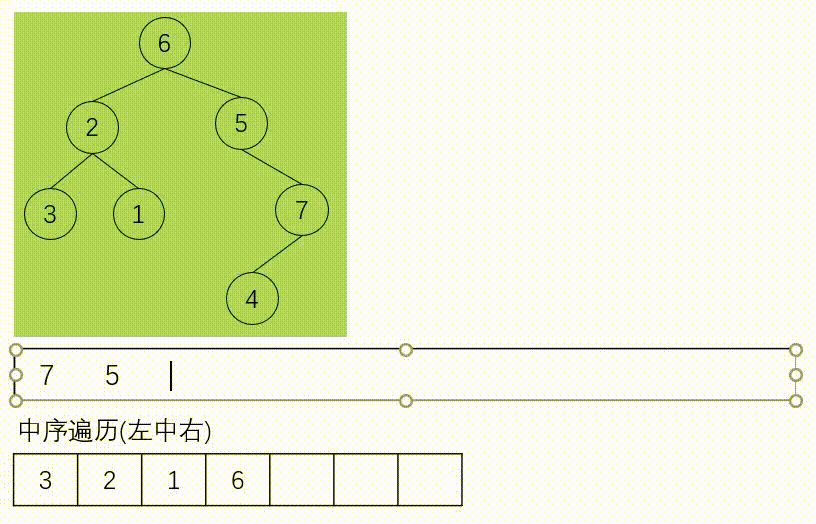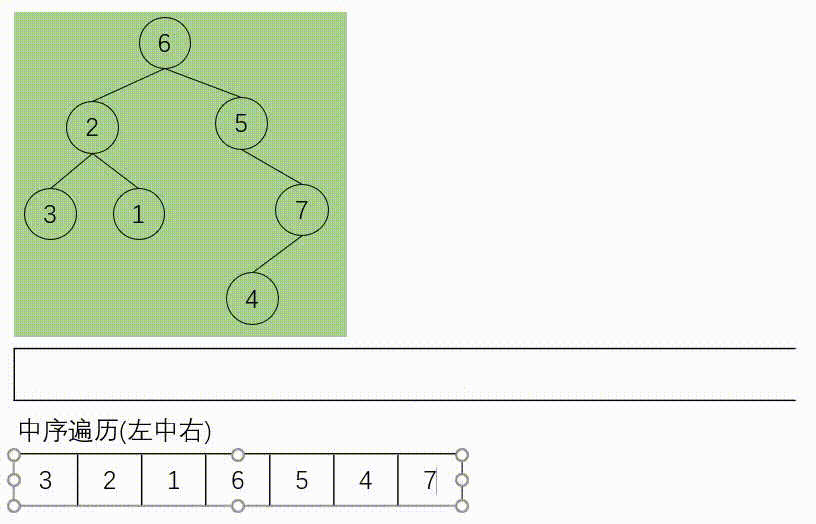
中序遍历(统一迭代法)
代码(C++):
//中序遍历(统一迭代) class Solution2 { public: vector<int> inorderTraversal(TreeNode* root) { stack<TreeNode*> sta; vector<int> result; if (root == nullptr) return result; else sta.push(root); while (!sta.empty()) { TreeNode* node = sta.top(); if (node != nullptr) { sta.pop(); //先将该节点弹出,避免重复操作 //遍历顺序:右-中null-左 //右节点不为空时入栈 if (node->right != nullptr) sta.push(node->right); //中间节点+标记 入栈 (中间节点访问过,但是还未处理) sta.push(node); sta.push(nullptr); //左节点不为空时入栈 if (node->left != nullptr) sta.push(node->left); } else { //当前节点为空时,将下一结果放入结果中 sta.pop(); result.push_back(sta.top()->val); sta.pop(); } } return result; } };
前序遍历(统一迭代法)
代码(C++):
//前序遍历(统一迭代) class Solution1 { public: vector<int> preorderTraversal(TreeNode* root) { stack<TreeNode*> sta; vector<int> result; if (root != nullptr) sta.push(root); while (!sta.empty()) { TreeNode* node = sta.top(); if (node != nullptr) { sta.pop(); //遍历顺序:右-左-中null if (node->right != nullptr) sta.push(node->right); if (node->left != nullptr) sta.push(node->left); sta.push(node); sta.push(nullptr); } else { sta.pop(); result.push_back(sta.top()->val); sta.pop(); } } return result; } };
后序遍历(统一迭代法)
代码(C++):
//后序遍历(统一迭代) class Solution3 { public: vector<int> postorderTraversal(TreeNode* root) { stack<TreeNode*> sta; vector<int> result; if (root != nullptr) sta.push(root); while (!sta.empty()) { TreeNode* node = sta.top(); if (node != nullptr) { //遍历顺序:中null-右-左 sta.push(nullptr); if (node->right != nullptr) sta.push(node->right); if (node->left != nullptr) sta.push(node->left); } else { sta.pop(); result.push_back(sta.top()->val); sta.pop(); } } return result; } };
参考链接