集合统计类期望题目。
题目描述
在一片大海上有 (n) 个岛屿,规划建设 (m) 座桥,第i座桥的成本为 (z_i),但由于海怪的存在,第 (i) 座桥有 (p_i) 的概率不能建造。
求在让岛屿尽量联通的情况下,期望最小成本为多少。
尽量联通:在对每座桥确定能否建造的情况下,对于任意两个岛屿,如果存在一种建桥方案使得它们联通,那么它们必须联通。
输入输出格式
输入格式:
第一行:两个整数 (n) 和 (m)((n) 为岛屿数量,(m) 为桥的数量),中间用空格分割。
之后 (m) 行,每行三个整数 (x_i,y_i,z_i) 和一个实数 (p_i),表示一条联通岛屿 (x_i) 与 (y_i) 的桥,成本为 (z_i),有 (p_i) 的概率损坏。保证不存在重边。
输出格式:
一行,一个实数 (ans),表示期望最小成本。输出保留6位小数。
输入输出样例
输入样例:
3 3 1 2 10 0.5 1 3 10 0.5 2 3 10 0.5输出样例:
13.750000说明
数据范围:
(nle 14, mle frac{n(n−1)}{2}, z_ile 100000, 0<p_i<1)
样例解释:
有 (frac 18) 的概率能建 (3) 座桥,那么尽量联通的最小代价是 (20)。
有 (frac 38) 的概率能建 (2) 座桥,那么尽量联通的最小代价是 (20)。
有 (frac 38) 的概率能建 (1) 座桥,那么尽量联通的最小代价是 (10)。
有 (frac 18) 的概率能建 (0) 座桥,那么尽量联通的最小代价是 (0)。
因此,总代价(=frac{1 imes 20+3 imes 20+3 imes 10+0}8=13.750000)。
题解:
集合一类的题目比较抽象,所以转移方程也有些难想。
首先我们考虑一条边在什么情况下会做出贡献。
理解题目中“尽量连通”的意思。对于一张图,如果两个点在原图上连通,那么要求他们在新图上必须连通。也就是求出最小生成森林。
因为相同权值的不同边对最小生成森林的最终结果互不影响,所以我们可以认为它们互不相同,对我们接下来的算法流程有一定的简化。首先按 (z_i) 排序,相同的 (z_i) 以下标为第二关键字。
那么一条边产生贡献当且仅当
- 它没有被破坏:(1-p_i),
- 不存在一条比它小的边连接 (x_i,y_i)。
令 (f[S]) 表示集合 (S) 是当前的一个极大最小生成树的概率。极大最小生成树表示不存在一条边 (left<u,v ight>) 使得 (uin S,v otin S) 且 (S) 内部互相连通。
对于一条边 (left<x_i,y_i ight>),枚举 (x_iin S,y_iin T) 的集合 (S) 和 (T),且 (Scap T=varnothing),则 (f[Scup T]) 的值与当前边就有了关系。如果之前没有连通,那么这条边会造成一个新的贡献;如果之前连通了,则不造成影响。所以 (f[Scup T]) 是加和关系。方程为 (f[Scup T]=f[Scup T]+f[S] imes f[T] imes P imes (1-p_i)),其中 (P) 是一个参数,表示重复计算的一些量,在下面会重提。
当这条边被摧毁时,二者均不变。方程表示为 (f[S]=f[S] imes p_i),这里没有上面的 (P),原因在于当 (f[S]) 这个值有意义时,就代表之前全部都合法。
此时我们进一步讨论“如果之前没有连通”的情况。事实上不连通只要满足 (Scap T=varnothing) 就可以了,看上去是直接贡献到答案的,但是需要考虑一些特殊的边。
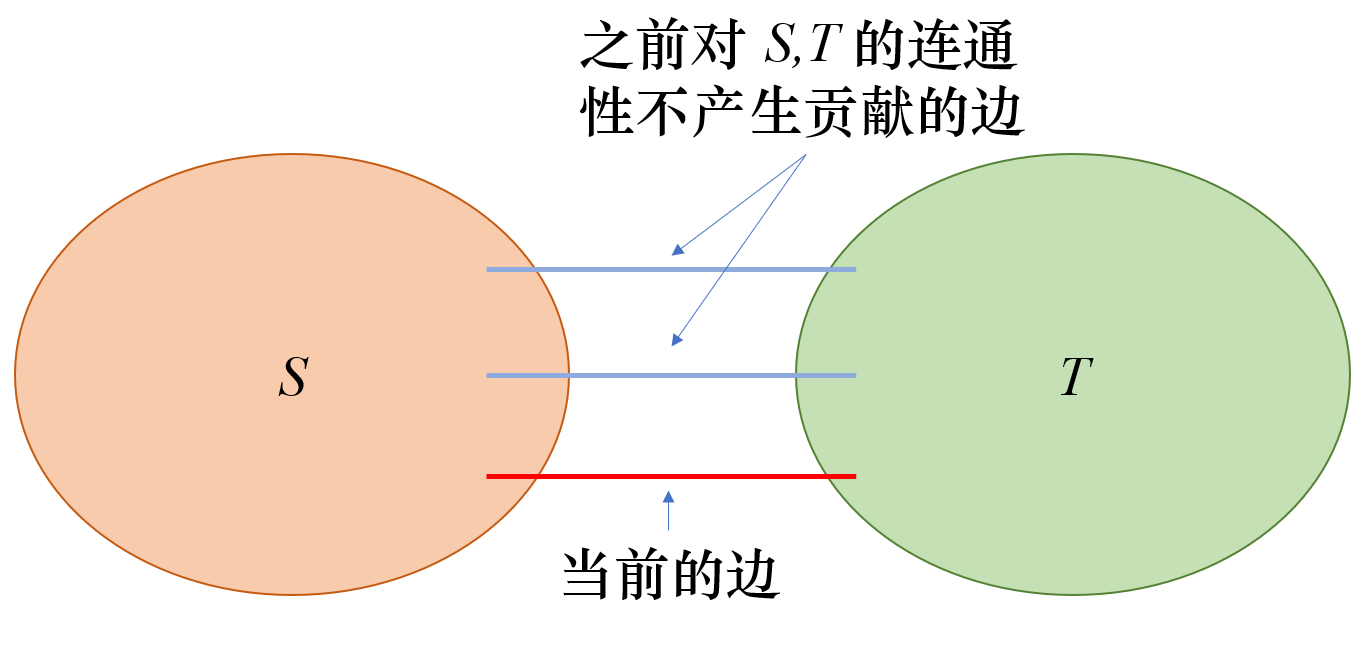
假设当前的边是红色,已经枚举到了 (S,T) 这两个集合。那么上面的蓝色边被摧毁时,分别在 (S) 和 (T) 处乘了 (p_i),但是实际上这样的边每条只出现了一次。因此在合并的时候我们要把它除掉,令 (g[S][T]) 表示
就是蓝色边的 (p) 的乘积。那么对于一条边以及它两边的集合 (S,T),它的 (P=g[S][T]),对答案的贡献就是 (f[S] imes f[T] imes P imes (1-p_i) imes z_i)。
此时考虑怎么算 (g[S][T]),你甚至无法开下一个 (2^{28}) 大小的数组。但是这个数可以 (O(1)) 计算或每次动态维护,这里给出 (O(1)) 的计算方法。
令 (h[S]) 表示 (S) 内部没有点互相连通的概率。对于第 (i) 条边,还是枚举左右的集合 (S,T)。(h[Scup T]) 仍不连通的概率是 (h[Scup T] imes p_i),注意这里和 (h[S],h[T]) 都没有关系。直观上理解是因为 (S) 和 (T) 之间可能还有一些边连接了,理性上分析原因是 (h[Scup P]) 如果仍不连通,那么之前一定不连通,同时当前这条边也没有做出贡献。(就这么简单)
然后发现 (h[Scup T]) 中的概率也是蓝色的边多算了一次,因此 (g[S][T]=frac{h[Scup T]}{h[S] imes h[T]})。然后枚举计算就可以了。
同时要注意 (f) 要满足无后效性,所以在更新完答案和一些无关的 (f,h) 后再更新一些不影响的 (f[S]=f[S] imes p_i)。
做了几个期望题..感觉到只要有任何一处细节错误就是 (100 o 0) 的节奏啊..省选应该不会主动开概率题的吧...
注意除法的常数极大,尽量转为乘法或者提前计算多次用到的数据。
由于枚举子集的子集复杂度为 (O(3^n)),所以总时间复杂度是 (O(mcdot 3^{n-2}))(题解说的。
(O(2^{|S|})) 枚举子集的方法可见博客置顶帖。
Code:
#include<cstdio>
#include<cstring>
#include<algorithm>
#define db double
struct edge
{
int x,y,z;
db p;
friend bool operator <(edge a,edge b)
{return a.z<b.z;}
}e[300];
db f[1<<14],h[1<<14];
//h是完全不连通概率
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i)
{
scanf("%d%d%d%lf",&e[i].x,&e[i].y,&e[i].z,&e[i].p);
--e[i].x;
--e[i].y;
}
std::sort(e+1,e+1+m);
for(int i=0;i<n;++i)
f[1<<i]=1;
for(int i=0;i<(1<<n);++i)
h[i]=1;
int U=(1<<n)-1;
db ans=0;
for(int i=1;i<=m;++i)
{
int x=1<<e[i].x,y=1<<e[i].y;
int s=U^x^y;
for(int j=s;j>=0;j=s&(j-1))
{
int t=U^j^x^y;
for(int k=t;k>=0;k=t&(k-1))
{
db g=f[j|x]*f[k|y]*(1-e[i].p)/h[j|x|k|y]*h[j|x]*h[k|y];
f[j|x|k|y]+=g;
ans+=g*e[i].z;
h[j|x|k|y]*=e[i].p;
if(!k)
break;
}
if(!j)
break;
}
for(int j=s;j>=0;j=s&(j-1))
{
f[j|x]*=e[i].p;
f[j|y]*=e[i].p;
if(!j)
break;
}
}
printf("%.6lf
",ans);
return 0;
}