ML_评价

如何评价模型的好坏。
学习目标有三个：数据拆分：训练数据集&测试数据集（西瓜书第二章）

　　

（一）数据拆分的原因：防止过拟合，即只有训练数据在模型中表现好，而之外的数据都会出现拟合较差的情况——泛化能力差

　　learning目的：寻找泛化误差小的模型，但是又依赖于经验误差——将样本集分为training &test（互斥），用test error近似泛化误差

　　常见split方法：

　　　1.　留出hold_out:直接将数据集D划分为两个互斥的集合

　　　　　　tips!training samples 和test samples的划分要尽可能保持数据分布的一致性，避免由于数据划分引起的偏差对结果产生影响。如——分层抽样

　　　　　　单次使用留出法得到的结果不可靠，一般采用若干次随机划分，每次都评估，留出法返回的是多个结果的平均

　　　　　　划分比例：若训练集S中包含绝大多数样本，则训练出来的模型会更加接近于D训练出来的模型，但是T比较小，评估结果可能会不稳定。若T中包含较多的样本，则S与D的差别较大，降低了评估的保真性fidelity。为了避免这些问题，常将2/3—4/5的样本用于training,剩下的testing

　　2.cross validation较差验证法

　　将D划分为k个大小相似，数据分布尽可能一致的互斥子集，（如分层），将K-个子集的并集作为training,剩余testing。则可以做k次检验，最终返回K次结果的均值

 　　留一法—K=n

　　3.自助法bootstrapping——减少训练样本规模变小的影响

　　bootstrap sample采样:每次都从D（m）中取出一个样本放到D‘中，最终D'中有m个样本

 调参：对每个参数选择范围和步长

最终模型：先用训练集进行评估测试，最后选定算法和参数，再用D重新训练模型，这就是提交给用户的最终模型

　　 在训练集上训练模型（参数），在验证集上评估模型，一旦找到的最佳的参数（超参数），就在测试集上最后测试一次，测试集上的误差作为泛化误差的近似。

　　吴恩达老师的视频中，如果当数据量不是很大的时候（万级别以下）的时候将训练集、验证集以及测试集划分为6：2：2；若是数据很大，可以将训练集、验证集、测试集比例调整为98：1：1；但是当可用的数据很少的情况下也可以使用一些高级的方法，比如留出方，K折交叉验证等。

#%%数据拆分开
#%%#0x01 判断模型好坏
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as  plt

iris=datasets.load_iris()
X=iris.data
y=iris.target
X.shape
y.shape
#拆分工作
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #方法一
#将X和y合并为同一个矩阵，然后对矩阵进行shuffle，之后再分解
#对y的索引进行乱序，根据索引确定与X的对应关系，最后再通过乱序的索引进行赋值
#shuffle() 方法将序列的所有元素随机排序。
tempConcat = np.concatenate((X, y.reshape(-1,1)), axis=1) #方法一
    #reshape(-1,1)表示行数自动计算，axis=1按列拼接
np.random.shuffle(tempConcat)
shuffle_X,shuffle_y = np.split(tempConcat, [4], axis=1) 
test_ratio = 0.2
test_size = int(len(X) * test_ratio) # 设置划分的比例
X_train = shuffle_X[test_size:]
y_train = shuffle_y[test_size:]
X_test = shuffle_X[:test_size]
y_test = shuffle_y[:test_size]

shuffle_index = np.random.permutation(len(X))  # 方法2
    # 将x长度这么多的数，返回一个新的打乱顺序的数组，注意，数组中的元素不是原来的数据，而是混乱的索引
test_ratio = 0.2
test_size = int(len(X) * test_ratio)# 指定测试数据的比例
test_index = shuffle_index[:test_size]
train_index = shuffle_index[test_size:]
X_train = X[train_index]
X_test = X[test_index]
y_train = y[train_index]
y_test = y[test_index]
y_test.shape
#
from sklearn.neighbors import KNeighborsClassifier
knn_0307=KNeighborsClassifier(n_neighbors=3)
knn_0307.fit(X_train,y_train)
y_predict=knn_0307.predict(X_test)

#对比
np.row_stack([y_predict,y_test])  #合并
#准确率
sum(y_predict == y_test) / len(y_test)
knn_0307.score(X_test,y_test)
#%%0x02 分类准确度accuracy
#数据探索
digits = datasets.load_digits() # 手写数字数据集，封装好的对象，可以理解为一个字段
X=digits.data
X.shape
y=digits.target
y.shape
digits.target_names#分类标签
# 去除某一个具体的数据，查看其特征以及标签信息
some_digit = X[666]
y[666]
some_digmit_image = some_digit.reshape(8, 8)
plt.imshow(some_digmit_image, cmap = plt.cm.binary)
plt.show()

#%%超参数：所谓超参数，就是在机器学习算法模型执行之前需要指定的参数。（调参调的就是超参数） 如kNN算法中的k
# 指定最佳值的分数，初始化为0.0；设置最佳值k，初始值为-1
best_score = 0.0
best_k = -1
for k in range(1, 11):  # 暂且设定到1～11的范围内
    knn_clf = KNeighborsClassifier(n_neighbors=k)
    knn_clf.fit(X_train, y_train)
    score = knn_clf.score(X_test, y_test)   
    if score > best_score:
        best_k = k
        best_score = score
print("best_k = ", best_k)
print("best_score = ", best_score)
#权重
#在 sklearn.neighbors 的构造函数 KNeighborsClassifier 中有一个参数：weights，默认是uniform即不考虑距离，也可以写distance来考虑距离权重
best_method = ""
best_score = 0.0
best_k = -1
for method in ["uniform","distance"]:    
    for k in range(1, 11):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method, p=2)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)        
        if score > best_score:
            best_k = k
            best_score = score
            best_method = method
print("best_method = ", method)
print("best_k = ", best_k)
print("best_score = ", best_score)

#网格搜索——一次性地把我们想要得到最好的超参数组合列出来
param_search = [
    { "weights":["uniform"], "n_neighbors":[i for i in range(1,11)] },
    { "weights":["distance"], "n_neighbors":[i for i in range(1,11)],"p":[i for i in range(1,6)]}
        ]
knn_clf = KNeighborsClassifier()# 调用网格搜索方法
from sklearn.model_selection import GridSearchCV
    # 定义网格搜索的对象grid_search，其构造函数的第一个参数表示对哪一个分类器进行算法搜索，第二个参数表示网格搜索相应的参数
grid_search = GridSearchCV(knn_clf, param_search)
grid_search.fit(X_train, y_train)
grid_search.best_estimator_
grid_search.best_score_

#随机划分
data = np.hstack([X,y[:,np.newaxis]])
#先将数据集进行拼接，要不然我们只针对样本进行采样的话，会找不到对应的标签的
train_set,test_set = train_test_split(data,test_size = 0.2,random_state = 42)
print(len(train_set),len(test_set))
#分层划分样本集
from sklearn.model_selection import StratifiedShuffleSplit

split = StratifiedShuffleSplit(n_splits = 1,test_size = 0.2,random_state = 42)

for train_index,test_index in split.split(data,data[:,-1]):
train_set = data[train_index,:]
test_set = data[test_index,:]

print(len(train_set),len(test_set))
#如果想要知道抽取的各个样本的比例——转换为dataframe
import pandas as pd
train_data = pd.DataFrame(train_set)
train_data.info()
#查看各个类别的比例-count函数
print(train_data[4].value_counts() / len(train_data))

（二）评价分类结果：精准度、混淆矩阵、精准率、召回率、F1 Score、ROC曲线等

1、分类算法的评价

　　对于一个回归问题，可以使用MSE、RMSE、MAE、R方。对于一个分类问题，可以使用分类精准度。但是实际上，分类精准度是存在陷阱的，有时候我们会需要更加全面的信息。

　　对于极度偏斜(Skewed Data)的数据，只使用分类准确度是不能衡量。这是就需要使用混淆矩阵(Confusion Matrix)做进一步分析。

　　混淆矩阵：第二个字母：What's your judgement about the sample?；第一个字母：Is your judgement right(true) or not(false)?

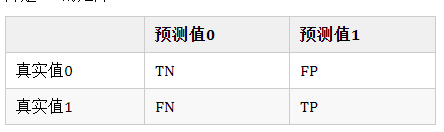
2、精准率和召回率

　　　　precesion = TP/(TP+FP) 即，查准率，检索结果中，都是你认为应该为正的样本（第二个字母都是P），但是其中有你判断正确的和判断错误的（第一个字母有T ，F）。通常更关注值为1的特征，比如“患病”，比如“有风险”。精准率为我们关注的那个事件，预测的有多准。

　　　　recall = TP/(TP+FN)即，查全率，检索结果中，你判断为正的样本也确实为正的，以及那些没在检索结果中被你判断为负但是事实上是正的（FN）。召回率也就是我们关注的那个事件真实的发生情况下，我们成功预测的比例是多少。

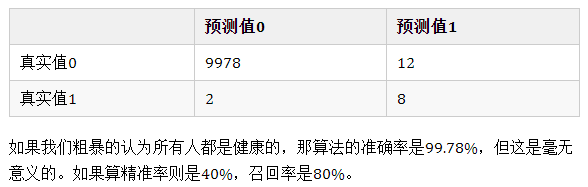
思考

①是否只关注accuracy？

虽然准确率可以判断总的正确率，但是如果存在样本不均衡的情况下，就不能使用accuracy来进行衡量了。比如，一个总样本中，正样本占90%,负样本占10%，那么只需要将所有样本预测为正，就可以拿到90%的准确率，而这显然是无意义的。正因为如此，我们就需要精准率和召回率了。

②那么精准率和召回率这两个指标如何解读？如果对于一个模型来说，两个指标一个低一个高该如何取舍呢？

精准率的应用场景：预测癌症。医生预测为癌症，患者确实患癌症的比例。

召回率的应用场景：网贷违约率，相对好用户，我们更关心坏用户。召回率越高，代表实际坏用户中被预测出来的概率越高。

例如对一般搜索的情况是在保证召回率的情况下提升准确率，而如果是疾病监测、反垃圾邮件等，则是在保证准确率的条件下，提升召回率。但有时候，需要兼顾两者，那么就可以用F-score指标

3、F1score_是调和平均数，只有两者都高的时候调和平均数才会高

4、ROC曲线受试者工作特征曲线 receiver operating characteristic curve ) 的简写，又称为感受性曲线(sensitivity curve)

　　阈值：为了将逻辑回归值映射到二元类别，您必须指定分类阈值（也称为判定阈值）。如果值高于该阈值，则表示“垃圾邮件”；如果值低于该阈值，则表示“非垃圾邮件”。人们往往会认为分类阈值应始终为 0.5，但阈值取决于具体问题，因此您必须对其进行调整 

　　横轴假正率（FP率），纵轴为真正率（TP率）-TPR和FPR之间是成正比的，TPR高，FPR也高。ROC曲线就是刻画这两个指标之间的关系。

TPR就是所有正例中，有多少被正确地判定为正；FPR是所有负例中，有多少被错误地判定为正。 分类阈值取不同值，TPR和FPR的计算结果也不同，最理想情况下，我们希望所有正例 & 负例 都被成功预测  TPR=1，FPR=0，即 所有的正例预测值 > 所有的负例预测值，此时阈值取最小正例预测值与最大负例预测值之间的值即可。

TPR越大越好，FPR越小越好，但这两个指标通常是矛盾的。为了增大TPR，可以预测更多的样本为正例，与此同时也增加了更多负例被误判为正例的情况。

ROC曲线是通过遍历所有阈值来描述整条曲线的。如果我们不断遍历所有阈值，预测的正样本与负样本数就在不断变化，相应的就会在ROC曲线移动。注意，此时ROC曲线本身的形状不会变化。

思考：

改变阈值并不会影响ROC曲线本身，那么如何判断ROC曲线的好坏？

重新回归到曲线本身，横轴是假正率，纵轴是真正率，我们希望在FP率低的情况下，TP率高。也就是说，ROC曲越陡越好

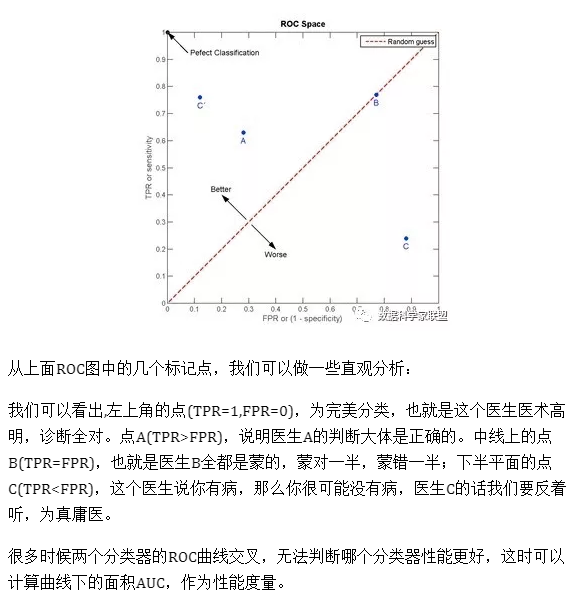
 5、AUC

一般在ROC曲线中，我们关注是曲线下面的面积， 称为AUC（Area Under Curve）。这个AUC是横轴范围（0,1 ），纵轴是（0,1）所以总面积是小于1的。

ROC和AUC的主要应用：比较两个模型哪个好？主要通过AUC能够直观看出来。

ROC曲线下方由梯形组成，矩形可以看成特征的梯形。因此，AUC的面积可以这样算：（上底+下底）* 高 / 2，曲线下面的面积可以由多个梯形面积叠加得到。AUC越大，分类器分类效果越好。

• AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样，模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

• #%%分类评价
  import numpy as np
  from sklearn import datasets
  from sklearn.model_selection import train_test_split
  from sklearn.linear_model import LogisticRegression
  
  digits=datasets.load_digits()
  X=digits.data
  y=digits.target.copy()
  y.shape
  # 要构造偏斜数据，将数字9的对应索引的元素设置为1，0～8设置为0
  y[digits.target==9]=1
  y[digits.target!=9]=0
  
  X_train,X_test,y_train,y_test=train_test_split(X, y, random_state=666)
  log_reg=LogisticRegression()
  log_reg.fit(X_train,y_train)
  y_log_predict=log_reg.predict(X_test)
  log_reg.score(X_test, y_test)
  #定义混淆矩阵的四个指标：TN
  def TN(y_true, y_predict):
      assert len(y_true) == len(y_predict)
      # (y_true == 0)：向量与数值按位比较，得到的是一个布尔向量
      # 向量与向量按位与，结果还是布尔向量
      # np.sum 计算布尔向量中True的个数(True记为1，False记为0)
      return np.sum((y_true == 0) & (y_predict == 0))  # 向量与向量按位与，结果还是向量
  TN(y_test, y_log_predict)
  
  #定义混淆矩阵的四个指标：FP
  def FP(y_true, y_predict):
      assert len(y_true) == len(y_predict)
      # (y_true == 0)：向量与数值按位比较，得到的是一个布尔向量
      # 向量与向量按位与，结果还是布尔向量
      # np.sum 计算布尔向量中True的个数(True记为1，False记为0)
      return np.sum((y_true == 0) & (y_predict == 1))  # 向量与向量按位与，结果还是向量
  FP(y_test, y_log_predict)
  
  #定义混淆矩阵的四个指标：FN
  def FN(y_true, y_predict):
      assert len(y_true) == len(y_predict)
      # (y_true == 0)：向量与数值按位比较，得到的是一个布尔向量
      # 向量与向量按位与，结果还是布尔向量
      # np.sum 计算布尔向量中True的个数(True记为1，False记为0)
      return np.sum((y_true == 1) & (y_predict == 0))  # 向量与向量按位与，结果还是向量
  FN(y_test, y_log_predict)
  #定义混淆矩阵的四个指标：TP
  def TP(y_true, y_predict):
      assert len(y_true) == len(y_predict)
      # (y_true == 0)：向量与数值按位比较，得到的是一个布尔向量
      # 向量与向量按位与，结果还是布尔向量
      # np.sum 计算布尔向量中True的个数(True记为1，False记为0)
      return np.sum((y_true == 1) & (y_predict == 1))  # 向量与向量按位与，结果还是向量
  TP(y_test, y_log_predict)
  #输出混淆矩阵
  def confusion_matrix(y_true, y_predict):
      return np.array([
          [TN(y_true, y_predict), FP(y_true, y_predict)],
          [FN(y_true, y_predict), TP(y_true, y_predict)]
      ])
  confusion_matrix(y_test, y_log_predict)
  #精准率
  def precision_score(y_true, y_predict):
      tp = TP(y_true, y_predict)
      fp = FP(y_true, y_predict)
      try:
          return tp / (tp + fp)
      except:
          return 0.0
  precision_score(y_test, y_log_predict)
  #召回率
  def recall_score(y_true, y_predict):
      tp = TP(y_true, y_predict)
      fn = FN(y_true, y_predict)
      try:
          return tp / (tp + fn)
      except:
          return 0.0
  recall_score(y_test, y_log_predict)
  # scikit-learn中的混淆矩阵，精准率和召回率
  from sklearn.metrics import confusion_matrix,precision_score,recall_score
  confusion_matrix(y_test,y_log_predict)
  precision_score(y_test,y_log_predict)
  recall_score(y_test,y_log_predict)
  #F1_SCORE
  import numpy as np
  def f1_score(precision, recall):
      try:
          return 2 * precision * recall / (precision + recall)
      except:
          return 0.0
  precision = 0.5
  recall = 0.5
  f1_score(precision, recall)
  precision = 0.9
  recall = 0.1
  f1_score(precision, recall)
  #decision_function，即返回分类阈值
  decision_scores = log_reg.decision_function(X_test)
  y_predict = np.array(decision_scores >= 5, dtype='int')  #大于等于5则为1
  
  # =============================================================================
  # #ROC
  # =============================================================================
  import numpy as np
  import matplotlib.pyplot as plt
  from sklearn import datasets
  from sklearn.model_selection import train_test_split
  from sklearn.linear_model import LogisticRegression
  
  digits = datasets.load_digits()
  X = digits.data
  y = digits.target.copy()
  
  # 要构造偏斜数据，将数字9的对应索引的元素设置为1，0～8设置为0
  y[digits.target==9]=1
  y[digits.target!=9]=0
  
  # 使用逻辑回归做一个分类
  X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
  
  log_reg = LogisticRegression()
  log_reg.fit(X_train,y_train)
  # 计算逻辑回归给予X_test样本的决策数据值
  # 通过decision_function可以调整精准率和召回率
  decision_scores = log_reg.decision_function(X_test)
  
  # TPR
  def TPR(y_true, y_predict):
      tp = TP(y_true, y_predict)
      fn = FN(y_true, y_predict)
      try:
          return tp / (tp + fn)
      except:
          return 0.0
  
  # FPR
  def FPR(y_true, y_predict):
      fp = FP(y_true, y_predict)
      tn = TN(y_true, y_predict)
      try:
          return fp / (fp + tn)
      except:
          return 0.0
  
  fprs = []    
  tprs = []
  
  # 以0.1为步长，遍历decision_scores中的最小值到最大值的所有数据点，将其作为阈值集合
  thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), 0.1)
  for threshold in thresholds:
      # decision_scores >= threshold 是布尔型向量，用dtype设置为int
      # 大于等于阈值threshold分类为1，小于为0，用这种方法得到预测值
      y_predict = np.array(decision_scores >= threshold, dtype=int)
      #print(y_predict)
      # print(y_test)
      #print(FPR(y_test, y_predict))
      # 对于每个阈值，所得到的FPR和TPR都添加到相应的队列中
      fprs.append(FPR(y_test, y_predict))
      tprs.append(TPR(y_test, y_predict))
      
  # 绘制ROC曲线，x轴是fpr的值，y轴是tpr的值
  plt.plot(fprs, tprs)
  plt.show()
  #SKLEARN中的roc
  from sklearn.metrics import roc_curve
  fprs, tprs, thresholds = roc_curve(y_test, decision_scores)
  plt.plot(fprs, tprs)
  plt.show()
  #sklearn中的auc
  from sklearn.metrics import roc_auc_score
  roc_auc_score(y_test,decision_scores)

（三）评价回归结果：MSE、RMSE、MAE、R Squared

1、均方误差MSE 

为了抵消掉数据量的形象，可以除去数据量，抵消误差。通过这种处理方式得到的结果叫做 均方误差MSE（Mean Squared Error）：

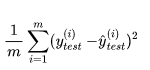
2、 均方根误差RMSE

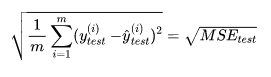
3、平均绝对误差MAE

 

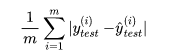
在之前确定损失函数时，我们提过，绝对值函数不是处处可导的，因此没有使用绝对值。但是在评价模型时不影响。因此模型的评价方法可以和损失函数不同。

4、R_square

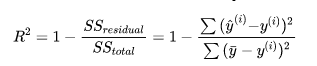
• 对于分子来说，预测值和真实值之差的平方和，即使用我们的模型预测产生的错误。
• 对于分母来说，是均值和真实值之差的平方和，即认为“预测值=样本均值”这个模型（Baseline Model）所产生的错误。
• 我们使用Baseline模型产生的错误较多，我们使用自己的模型错误较少。因此用1减去较少的错误除以较多的错误，实际上是衡量了我们的模型拟合住数据的地方，即没有产生错误的相应指标。

 

#%%波士顿放假——回归评价
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 查看数据集描述
boston = datasets.load_boston()
print(boston.DESCR)
# 查看数据集的特征列表
boston.feature_names
#RM average number of rooms per dwelling 每个住宅的平均房间数 选一个特征建模
x = boston.data[:,5]
x.shape
# 取出样本标签
y = boston.target
y.shape
plt.scatter(x,y)
#数据清洗——去掉50

np.max(y)
# 这里有一个骚操作，用比较运算符返回一个布尔值的向量，将其作为索引，直接在矩阵里对每个元素进行过滤。
x = x[y < 50.0]
y = y[y < 50.0]
plt.scatter(x,y)
plt.show()
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.3)
y.shape
x.shape
from sklearn import linear_model
reg=linear_model.LinearRegression()
reg.fit(x_train.reshape(-1, 1),y_train)
reg.intercept_
reg.coef_
y_predict = reg.predict(x_test.reshape(-1, 1))
print(y_predict)
# =============================================================================
#MSE
mse_test = np.sum((y_predict - y_test) ** 2) / len(y_test)
mse_test

from math import sqrt
rmse_test = sqrt(mse_test)
rmse_test
#MAE
mae_test = np.sum(np.absolute(y_predict - y_test)) / len(y_test)
mae_test
#SKLEARN
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
mean_squared_error(y_test, y_predict)
mean_absolute_error(y_test,y_predict)
# =============================================================================
#r^2
1 - mean_squared_error(y_test, y_predict) / np.var(y_test)
from sklearn.metrics import r2_score
r2_score(y_test, y_predict)