目录
什么是因子分析
因子分析法是指从研究指标相关矩阵内部的依赖关系出发，把一些信息重叠、具有错综复杂关系的变量归结为少数几个不相关的综合因子的一种多元统计分析方法。基本思想是：根据相关性大小把变量分组，使得同组内的变量之间相关性较高，但不同组的变量不相关或相关性较低，每组变量代表一个基本结构一即公共因子。
因子分析法的步骤
应用因子分析法的主要步骤如下：
(1)对数据样本进行标准化处理。
(2)计算样本的相关矩阵R。
(3)求相关矩阵R的特征根和特征向量。
(4)根据系统要求的累积贡献率确定主因子的个数。
(5)计算因子载荷矩阵A。
(6)确定因子模型。
(7)根据上述计算结果，对系统进行分析。
因子分析法的实例 [1]
【例：1】
假设某一社会经济系统问题，其主要特性可用4个指标表示，它们分别是生产、技术、交通和环境。其相关矩阵为：
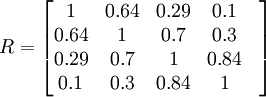
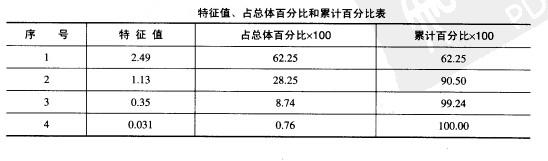
相应的特征值、占总体百分比和累计百分比如下表：
对应特征值的特征向量矩阵为：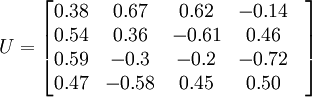 
假如要求所取特征值反映的信息量占总体信息量的90％以上，则从累计特征值所占百分比看，只需取前两项即可。也就是说，只需取两个主要因子。对应于前两列特征值的特征向量，
可求的其因子载荷矩阵A为：
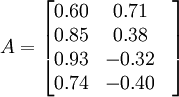
于是，该问题的因子模型为：
Xl = 0.60f1 + 0.71f2
X2 = 0.85f1 + 0.38f2
X3 = 0.93f1 − 0.32f2
X4 = 0.74f1 − 0.40f2
由以上可以看出，两个因子中，f1是全面反映生产、技术、交通和环境的因子，而f2却不同，它反映了对生产和技术这两项增长有利，而对交通和环境增长不利的因子。也就是说，按照原有统计资料得出的相关矩阵分析的结果是如果生产和技术都随f2增长了，将有可能出现交通紧张和环境恶化的问题，f2反映了这两方面的相互制约状况。
因子分析与主成分分析的区别 [2]
因子分析法与主成分分析法都属于因素分析法，都基于统计分析方法，但两者有较大的区别：主成分分析是通过坐标变换提取主成分，也就是将一组具有相关性的变量变换为一组独立的变量，将主成分表示为原始观察变量的线性组合；而因子分析法是要构造因子模型，将原始观察变量分解为因子的线性组合。通过对上述内容的学习，可以看出因子分析法和主成分分析法的主要区别为：
(1)主成分分析是将主要成分表示为原始观察变量的线性组合，而因子分析是将原始观察变量表示为新因子的线性组合，原始观察变量在两种情况下所处的位置不同。
(2)主成分分析中，新变量Z的坐标维数j(或主成分的维数)与原始变量维数相同，它只是将一组具有相关性的变量通过正交变换转换成一组维数相同的独立变量，再按总方差误差的允许值大小，来选定q个(q<p)主成分；而因子分析法是要构造一个模型，将问题的为数众多的变量减少为几个新因子，新因子变量数m小于原始变量数P，从而构造成一个结构简单的模型。可以认为，因子分析法是主成分分析法的发展。
(3)主成分分析中，经正交变换的变量系数是相关矩阵R的特征向量的相应元素；而因子分析模型的变量系数取自因子负荷量，即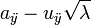
。因子负荷量矩阵A与相关矩阵R满足以下关系：
其中，U为R的特征向量。
在考虑有残余项ε时，可设包含εi的矩阵ρ为误差项，则有R − AAT = ρ。
在因子分析中，残余项应只在ρ的对角元素项中，因特殊项只属于原变量项，因此，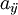
的选择应以ρ的非对角元素的方差最小为原则。而在主成分分析中，选择原则是使舍弃成分所对应的方差项累积值不超过规定值，或者说被舍弃项各对角要素的自乘和为最小，这两者是不痛的。
相关条目
参考文献
本条目相关文档
from：《《多元统计分析》》
转自：MBA智库百科 http://wiki.mbalib.com/wiki/%E5%9B%A0%E5%AD%90%E5%88%86%E6%9E%90%E6%B3%95