【等距螺旋的别名是等速度比螺旋】
等距螺旋的公式中,直线速度w与圆周速度v并不独立出现,而是以速度比的形式出现,如下所示:
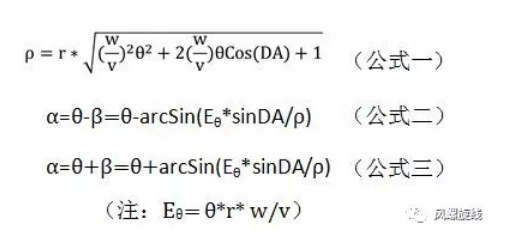
- 等距螺旋中存在突变点,突变点对应的角度为-v/(w*CosDA)。
(注:由于v与w均为正值,DA角范围为(-90°,90°)因此,突变点仅出现在负值区间。由于螺旋的对称效应,可使用-α来代表与α方向相反的螺旋,计算时按α>0来分析。)
- 从圆周移动到近地点,共需要经历的旋转角度为v*cosDA/w(弧度单位)。
通过以上的这些计算都可以看到,直线速度与基圆速度的比值可以用来判断螺旋是否是等距离外扩(比值恒定为等距螺旋,不恒定为非等距螺旋),或者螺旋是否相同(不同的速度搭配,若速度比值相同即为同一条螺旋)。
当旋转速度加倍,直线速度同时也加倍的情况下,速度的比值没有发生变化,即螺旋的公式将不会发生变化,也就是说速度同时加倍的情况下,仍属于同一条螺旋。渐开线打开的快慢,并不影响它的螺旋轨迹的大小,就是这一原理的最佳证据。
再回到阿基米德螺旋的一个经典案例,小虫匀速从唱片的中心向外爬去。小虫越向外走,我们观察到的小虫的弧线速度是在增加的,但它所形成的螺旋轨迹却是等距离外扩的。在这里,小虫的直线速度对应的基圆速度(阿基米德螺旋并未提到基圆的概念,但它是真实存在的)之比是固定的,因此,它属于等距离外扩的螺旋。小虫的直线运动穿过圆心,因此,螺旋轨迹属于等距螺旋中的阿基米德螺旋。
在小虫与唱片这样的旋转系统中,小虫与唱片之间存在摩擦力,这种摩擦力使得小虫的弧线速度在不断的增加,当小虫从唱片外沿掉落的时候,它的速度相当于唱片外沿的速度与直线爬行速度的叠加。小虫的直线爬行速度与基圆速度相绑定,与它实际的空间速度无关。唱片每一个旋转周期的时间是固定的,传统的分析中引入了角动量的概念,而角动量可以线性的转化为基圆速度v,从速度比的角度来看,它们的速度比是一个固定值,因此属于等距螺旋。
【非等距螺旋的联想】
(直线运动与圆周运动的)速度比恒定的情况下会产生等距离外扩螺旋,那么速度比均匀增加或均匀减小的情况下,必然出现加速度外扩(或是收缩)的螺旋,它些螺旋可以统称为非等距螺旋。

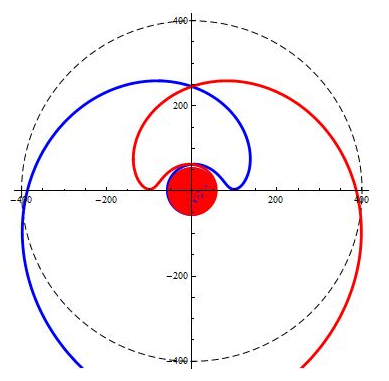
如果我们的宇宙处于某个非等距螺旋轨道上,周围的星体也同样位于这样的轨道中。那么,当这个旋转系统的旋转速度在减慢,而直线速度并未变化的情况下,从我们观察的角度来看,会发现世界在加速膨胀。因为,我们进入了螺旋的发散阶段,各个星体轨迹之间的微小差异,都会在不断的放大。从这样的角度来看,宇宙的膨胀并不需要外力来支持,而只是我们所处的世界旋转的更慢了一些而已。

前面两张图形实际上是数学公式出错的产物,非等距螺旋的分析是等距螺旋理论的进一步延伸,我们只是站在它的门口向里面望了一眼而已。古人云“吾生也有涯,而知也无涯。以有涯随无涯,殆已”,所以这个方向的讨论留给对数学感兴趣的朋友们继续吧。
【为什么会有突变点】
在等距螺旋的公式里,角度进入到负值区间的某个位置时,会出现突变,螺旋轨迹会进入到它的互补螺旋的轨迹中去。那么,为什么会有突变点呢?
首先,这是数学公式的不完美造成的。当我们试图用单一公式来表达顺时针外扩与逆时针外扩的螺旋时,就会发现在某个位置,公式出现了“错误”。所以对于数学公式应保持警惕的态度,在没有对参数区间进行完整论证之前,不要先入为主的以为数据是平滑安全的。
其次,这是由于螺旋的互补性造成的。在螺旋的世界里顺时针旋转的螺旋与逆时针旋转的螺旋互补,它们在角度关系与表达式上是非常近似的。二者角度之间相差180度,突变点的计算过程也正好符合这样的一种设定。
从科幻的角度来说,电影、小说里对于时空穿越点的描述已经是常态化的标配了,突变点的存在非常默契的配合了这样的题材。尽管我个人对时空穿越持怀疑态度(少部分人的穿越,让全世界来陪同,这个能量消耗不科学啊),但如果这样能帮助我们更好的理解突变点,倒也不妨按这个思路去想象一下。
【等距螺旋的过去、现在和未来】
阿基米德(公元前287年—公元前212年)在距今两千两百多年前将“螺线”定义为一个匀速运动的点沿直线从圆心向外运动,直线同时进行匀速旋转时,动点所形成的螺旋状曲线。由于最初的这种定义,很多人以为只有匀速运动才能得到螺旋,故又将它称为等速螺旋。
网上搜索渐开线起源,几乎全部与齿轮相关,真实的出现年代反而无从考证。齿轮最早在公元前400年至200年出现在中国,1694年法国科学家Philippe首先提出渐开线可作为齿形曲线,此后渐开线在齿轮加工领域里得到了逐步的发展。新中国成立之初,我们几乎没有现化化齿轮的加工能力,经过很多人的努力,最终形成了完整的加工体系。
风螺旋(wind spiral)是随着航空工业的发展而引入的一种螺旋,在上个世纪开始的国际民航组织8168文件中,对风螺旋进行了描述,它假想航空器在转弯过程中,受到累积风的影响而形成的螺旋状的最大外边界。国际民航组织并未对风螺旋给出相应的计算公式,这使得飞行程序保护区在自动化绘制时遇到了非常大的困难。不少人使用阿基米德螺旋来代替风螺旋,除了极易产生范围偏小或者精度不够的情况外,等距外扩、切线与公切线的计算都走入了死胡通。
2014年8月,《风螺旋线的深度分析》一文在《空中交通》杂志正式刊发,文中列出的风螺旋公式就是后来的等距螺旋公式1与公式2。此后,相继完成了传统程序保护区的算法分析,论文选题覆盖了程序转弯(2017年)、基线转弯(2017年)、等待程序(2018年)。算法中解决了切线与公切线的计算,并且非常简单的实现了等距外扩的计算。
在传统程序保护区分析论证的基础之上,通过对风螺旋的算法进行全面的回顾整理,对照其它的典型螺旋进行分析,最终发现风螺旋公式在特定角度条件下,可以成功的转换为阿基米德公式以及渐开线公式,从运动形式到计算方法,实现了螺旋概念的统一。2018年6月《数学的实践与认识》刊发了《等距螺旋的原理与计算》,标志着全新的螺旋概念的形成。文章中对典型螺旋的公式转换方法进行了详细的分析,证明了风螺旋并不是一个孤立的存在,而是等距螺旋的通用公式。

2019年,风螺旋在PBN中的算法应用文章将陆续刊发,实现从传统程序向PBN保护区算法的跨越。未来随着PBN技术的广泛应用,风螺旋算法在飞行程序中必将取得更广阔的发展空间。
【等距螺旋的特性】
当我们观察一条“完整”的等距螺旋时,我们首先会发现它是轴对称图形,也就是说完整的螺旋具备对称性。
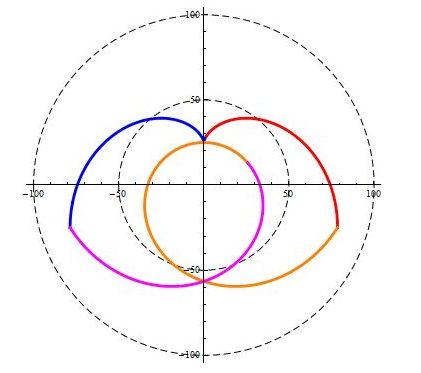
其次,正向旋转与反向旋转,会得到两条互补的螺旋,它们会在近地点的位置相切,这是螺旋所体现出的互补性。互补的两条螺旋在公式表达上,也体出了互换的特点,当螺旋经过突变点时,正向螺旋的公式会与反向螺旋的公式互换,并且按照交换后的公式继续发展。
基础参数相同的等距螺旋,无论它们出发时的角度有多么不同,经过多个周期的旋转外扩之后,它们看起来都会非常的相似,这体现了等距螺旋的趋同性。
【等距螺旋的哲学意义】
我们的世界中随处可见螺旋的影子,让人不禁猜想,大的宇宙体系是否也是某种螺旋扩散的结构。
从完整的螺旋运动轨迹来看,世界可以从无限远处逐渐旋转收缩,到达最接近圆心的位置(近地点)后,再继续旋转放大,去向无限远的地方。这种不知道起点、终点的状况,用“无所从来,无所从往”来描述最恰当不过。虽然不知道起点、终点,但从螺旋的轨迹上可以确定的是,我们从哪里来,必将回到哪里去。
我们已知宇宙进入了膨胀的周期,这意味着经过了收缩周期(如果有的话)之后,我们已经是在“回去”的路上了。剩下的唯一问题就是时间,宇宙仅仅是膨胀以来的时间就有大约150亿年,如果“来时”用了相同的时间,那么回去也该差不多的时间才可以。在这个漫长而孤独的星际旅行里,照顾好自己,照顾好身边的人,照顾好我们的星球就是最基本的生命意义。
回到个体的角度来看,在运动方式固定的情况下,所有的螺旋最终都是相似的。这意味没有所谓的捷径,坚持各自的方向就是最佳的选择,“万千法门皆可得道”说的就是这种情形。正如大多数人的生活一样,走过的路或许不同,但生命的轨迹却一定是相似的。
感谢您阅读至此,今天的文字超长,是因为在终结这个系列的话题之前,想说的话还有太多。今天的很多内容已经是未经实验,仅供猜想的成分了。简单来说,等距螺旋的研究还有很多方向,但时间和精力的关系,只能先止步于此了。后续我们将集中精力,回到飞行程序算法分析的轨道上去,力争在风螺旋算法的推广之路上走得更远,飞得更高。