Tensorflow2.0笔记
本博客为Tensorflow2.0学习笔记,感谢北京大学微电子学院曹建老师
5 扩展方法
5.1 本地读取鸢尾花数据集
在这部分我们尝试从本地读取鸢尾花数据集的 txt 文件,并将其输入至神经网络进行训练。鸢尾花数据集的 txt 文件包含内容如图 5.1 所示。
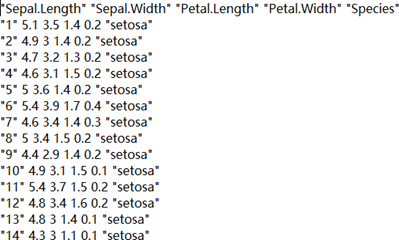
图 5.1 鸢尾花数据集 txt 文件内容
(1) 利用 pandas 中函数读取,并处理成神经网络需要的数据结构,即利用pd.read_csv('文件名',header=第几行作为表头,sep='分割符号')
(2)利用 open 函数打开 txt 文件,并处理成神经网络需要的数据结构,即利用 open('文件名','r')。
利用 pandas 中函数读取方法如下:
df = pd.read_csv('iris.txt',header = None,sep=',') #读取本地文件
data = df.values # 去掉索引并取值
x_data = [lines[0:4] for lines in data] # 取输入特征
x_data = np.array(x_data,float) # 转换为 numpy 格式
y_data = [lines[4] for lines in data] # 取标签
for i in range(len(y_data)):
if y_data[i] == 'Iris-setosa':
y_data[i] = 0
elif y_data[i] == 'Iris-versicolor':
y_data[i] = 1
......
y_data = np.array(y_data)
即通过读取本地文件、取特征输入、取标签并将其转换为规定格式,实现本地数据集的读取。
利用 open 函数读取方法如下:
f = open('iris.txt','r') # 取本地文件
contents = f.readlines() # 按行读取
i=0
for content in contents:
temp = content.split(',') # 按逗号分隔
x_data[i] = np.array([temp[0:4]],dtype=float) # 取输入特征
if temp[4] == 'Iris-setosa
': # 判断标签并赋值
y_data[i] = 0
elif temp[4] == 'Iris-versicolor
':
y_data[i] = 1
......
i = i + 1
即通过读取本地文件、分割、取输入特征、取标签,实现本地数据集的读取。
5.2 搭建神经网络
数据集较为简单,可利用简单网络结构进行拟合,仅考虑输入层与输出层, 构建单层神经网络。参数定义如下:
w1 = tf.Variable(tf.random.truncated_normal[4,3],stddev = 0.1,seed = 1))
b1 = tf.Variable(tf.random.truncated_normal[3],stddev = 0.1,seed = 1))
将学习率设置为 0.5,训练后可发现出现梯度爆炸,网络不能有效收敛,训练过程 loss 曲线如图 5.2。
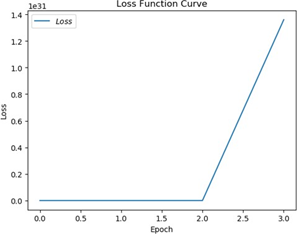
图 5.2 梯度爆炸时 loss 曲线
分析产生梯度爆炸的原因,考虑到使用梯度下降思想时,其计算公式为

参数更新量为学习率与损失函数偏导数相乘,二者乘积过大,则会导致梯度爆炸。因此,解决梯度爆炸问题可针对学习率进行调整,也可对数据进行调整。故解决方法可为:(1)逐步减小学习率,0.1、0.01 等;(2)对数据进行预处理后再输入神经网络,减小偏差值的大小,抑制梯度爆炸,即数据归一化与标准化,其主要方法有线性归一化、非线性归一化、Z-Score 标准化。
线性归一化将数据映射到[0,1]区间中,计算公式如下:
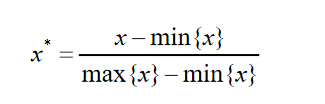
非线性归一化(log 函数转换)使数据映射到[0,1]区间上,计算公式如下:

Z-Score 标准化使每个特征中的数值平均值变为 0,标准差变为 1,计算公式如下:
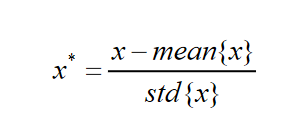
以线性归一化为例,其代码实现如下:
def normalize(data):
x_data = data.T # 每一列为同一属性,转置到每一行
for i in range(4):
x_data[i] = (x_data[i] - tf.reduce_min(x_data[i])) /
(tf.reduce_max(x_data[i]) - tf.reduce_min(x_data[i]))
return x_data.T # 转置回原格式
5.3优化
做完数据标准化,上述网络已经可以跑通,下面对网络进行部分优化,增加指数衰减学习率,指数衰减学习率可在训练初期赋予网络较大学习率,并在训练过程中逐步减小,可有效增加网络收敛速度,其在 tensorflow 中对应函数为tf.compat.v1.train.exponential_decay(learning_rate_base,global_step,decay_step,deca y_rate,staircase =True(False),name),当 staircase 为 True 时,学习率呈现阶梯状递减。
做完优化后,对网络进行训练。笔者采用 Z-score 标准化后训练 1000 个 eopch,当 staircase =True 时,其 loss、准确率、学习率曲线如图 5.3 所示。
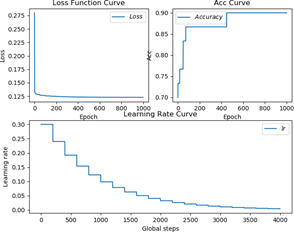
图 5.3 staircase =True 训练过程准确率曲线
当 staircase =False 时,其 loss、准确率、学习率曲线如图 5.4 所示。
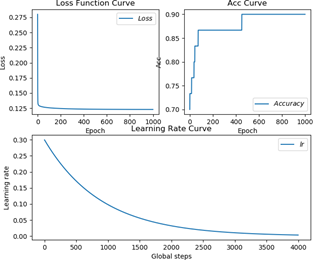
图 5.4 staircase =False 训练过程准确率曲线