Codeforces-698B Fix a Tree

A tree is an undirected connected graph without cycles.

Let's consider a rooted undirected tree with n vertices, numbered 1 through n. There are many ways to represent such a tree. One way is to create an array with n integers p1, p2, ..., pn, where pi denotes a parent of vertex i (here, for convenience a root is considered its own parent).

For this rooted tree the array p is [2, 3, 3, 2].

Given a sequence p1, p2, ..., pn, one is able to restore a tree:

1. There must be exactly one index r that pr = r. A vertex r is a root of the tree.
2. For all other n - 1 vertices i, there is an edge between vertex i and vertex pi.

A sequence p1, p2, ..., pn is called valid if the described procedure generates some (any) rooted tree. For example, for n = 3 sequences(1,2,2), (2,3,1) and (2,1,3) are not valid.

You are given a sequence a1, a2, ..., an, not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.

Input

The first line of the input contains an integer n (2 ≤ n ≤ 200 000) — the number of vertices in the tree.

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n).

Output

In the first line print the minimum number of elements to change, in order to get a valid sequence.

In the second line, print any valid sequence possible to get from (a1, a2, ..., an) in the minimum number of changes. If there are many such sequences, any of them will be accepted.

Examples

input

4
2 3 3 4

output

1
2 3 4 4 

input

5
3 2 2 5 3

output

0
3 2 2 5 3 

input

8
2 3 5 4 1 6 6 7

output

2
2 3 7 8 1 6 6 7

Note

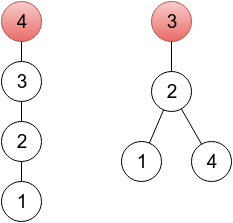
In the first sample, it's enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex 4(because p4 = 4), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex 3 (right drawing below). On both drawings, roots are painted red.

In the second sample, the given sequence is already valid.

题目大意：

给你一棵树，但是这棵树不一定是一个合法的树，不合法的情况有

1.存在回路

2.不连通

问你最少的操作使得这个树合法，并输出这个树，如果有多个随意输出一个即可

解题思路：

并查集或者DFS或者BFS都是可以的，比较推荐并查集。

代码：

#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 2e5 + 5;
int n, p[maxn], pre[maxn];

int findfather(int x){
    return pre[x] = (pre[x] == x ? pre[x] : findfather(pre[x]));
}
int main()
{
    scanf("%d", &n);
    int ans = 0, root = 0;
    for(int i = 1; i <= n; ++i) pre[i] = i;
    for(int i = 1; i <= n; ++i){
        scanf("%d", &p[i]);
        if(p[i] == i){
            root = i;
            ++ans;
        }else{
            int fx = findfather(i);
            int fy = findfather(p[i]);

            if(fx == fy){
                p[i] = i;
                ++ans;
            }else pre[fx] = fy;
        }
    }

    if(root == 0){
        for(int i = 1; i <= n; ++i) if(p[i] == i) root = i;
        ++ans;
    }

    printf("%d
", ans - 1);
    for(int i = 1; i <= n; ++i){
        if(i != 1) printf(" ");
        if(p[i] == i) p[i] = root;
        printf("%d", p[i]);
    }
    puts("");
    return 0;
}