对于二分类问题:
对于结果是0或1(正或负)的数据集,利用线性回归算法用直线对数据进行拟合:设置一个分类器输出的阈值(0.5),当样本分布不均时,效果可能不会很好;
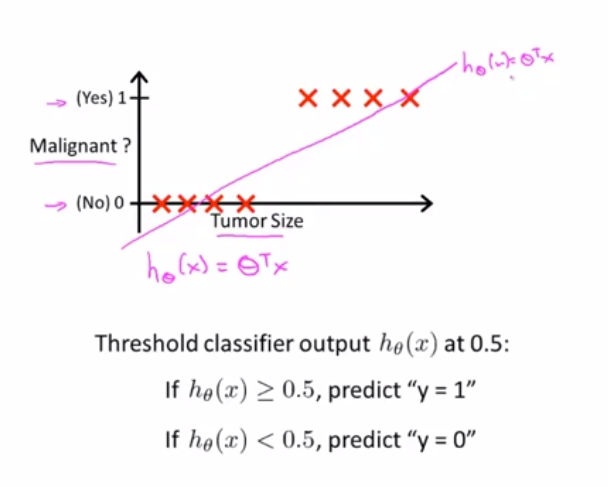

图1 拟合效果 图2 横轴延长增加一个不太重要的样本,效果却变差了
logistic Regression:算法的输出或者预测值一直介于0和1之间,不会大于或小于0,这是一种分类算法,命名中的“回归”可能会令人困惑,但实际logistic回归是用于离散分类的:y=0 or y=1。
sigmoid函数/logisitc函数:1/(1+e-x)
代码实现:
import numpy as np
import math
from matplotlib import pyplot as plot
def sigmoid_logs_function(x):
return 1./(1 + np.exp(-x))
if __name__ =='__main__':
sl = np.arange(-10,10,0.01)#创建等差数组,(开始,结束,步长)
fsl = sigmoid_logs_function(sl)
plot.title("Sigmoid Function")
plot.xlabel('d')
plot.ylabel('y(d)')
plot.plot(sl, fsl)
plot.show()
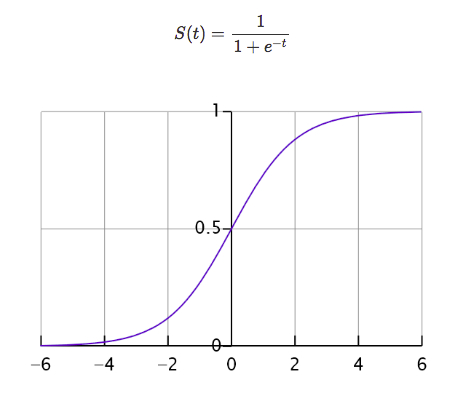
用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点:
优点:平滑、易于求导。
缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
损失函数
机器学习中,对模型的训练都是对loss function 进行优化。分类问题中 ,一般使用极大似然估计来构造损失函数。对损失函数求极大/极小值,得到参数估计值。
Logistic回归采用交叉熵作为损失函数,并使用梯度下降法来对参数进行优化。
Logistic回归常用的优化方法:
一阶:梯度下降、随机梯度下降、mini 随机梯度下降降法。随机梯度下降不但速度上比原始梯度下降要快,局部最优化问题时可以一定程度上抑制局部最优解的发生。
二阶:牛顿法,拟牛顿法;
这里详细说一下牛顿法的基本原理和牛顿法的应用方式。牛顿法其实就是通过切线与x轴的交点不断更新切线的位置,直到达到曲线与x轴的交点得到方程解。在实际应用中我们因为常常要求解凸优化问题,也就是要求解函数一阶导数为0的位置,而牛顿法恰好可以给这种问题提供解决方法。实际应用中牛顿法首先选择一个点作为起始点,并进行一次二阶泰勒展开得到导数为0的点进行一个更新,直到达到要求,这时牛顿法也就成了二阶求解问题,比一阶方法更快。我们常常看到的x通常为一个多维向量,这也就引出了Hessian矩阵的概念(就是x的二阶导数矩阵)。
缺点:牛顿法是定长迭代,没有步长因子,所以不能保证函数值稳定的下降,严重时甚至会失败。还有就是牛顿法要求函数一定是二阶可导的。而且计算Hessian矩阵的逆复杂度很大。
拟牛顿法: 不用二阶偏导而是构造出Hessian矩阵的近似正定对称矩阵的方法称为拟牛顿法。拟牛顿法的思路就是用一个特别的表达形式来模拟Hessian矩阵或者是他的逆使得表达式满足拟牛顿条件。主要有DFP法(逼近Hession的逆)、BFGS(直接逼近Hession矩阵)、 L-BFGS(可以减少BFGS所需的存储空间)。
逻辑斯特回归为什么要对特征进行离散化
- 非线性!非线性!非线性!逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合; 离散特征的增加和减少都很容易,易于模型的快速迭代;
- 速度快!速度快!速度快!稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
- 鲁棒性!鲁棒性!鲁棒性!离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
- 方便交叉与特征组合:离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
- 稳定性:特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
- 简化模型:特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。