1301. Number of Paths with Max Score

You are given a square board of characters. You can move on the board starting at the bottom right square marked with the character 'S'.

You need to reach the top left square marked with the character 'E'. The rest of the squares are labeled either with a numeric character 1, 2, ..., 9 or with an obstacle 'X'. In one move you can go up, left or up-left (diagonally) only if there is no obstacle there.

Return a list of two integers: the first integer is the maximum sum of numeric characters you can collect, and the second is the number of such paths that you can take to get that maximum sum, taken modulo 10^9 + 7.

In case there is no path, return [0, 0].

Example 1:

Input: board = ["E23","2X2","12S"]
Output: [7,1]

Example 2:

Input: board = ["E12","1X1","21S"]
Output: [4,2]

Example 3:

Input: board = ["E11","XXX","11S"]
Output: [0,0]

Constraints:

• 2 <= board.length == board[i].length <= 100

class Solution {
    public int[] pathsWithMaxScore(List<String> board) {
        int MOD = (int)(1e9 + 7);
        int m = board.size();
        int[][] dp = new int[m+1][m+1];
        int[][] cc = new int[m+1][m+1];
        cc[m-1][m-1] = 1;
        for(int i = m-1;i>=0;i--)
            for(int j = m-1; j>=0;j--){
                char c= board.get(i).charAt(j);
                if(c!='X'){
                    int max = Math.max(Math.max(dp[i+1][j], dp[i][j+1]), dp[i+1][j+1]);
                    int num = c-'0';
                    if(c=='S' || c=='E') num = 0;
                    dp[i][j] = num + max;
                    if(dp[i+1][j] == max) cc[i][j] = (cc[i][j] + cc[i+1][j]) % MOD;
                    if(dp[i+1][j+1] == max) cc[i][j] = (cc[i][j] + cc[i+1][j+1]) % MOD;
                    if(dp[i][j+1] == max) cc[i][j] = (cc[i][j] + cc[i][j+1]) % MOD;
                }
            }
        
        return cc[0][0] > 0 ? new int[]{dp[0][0], cc[0][0]} : new int[]{0, 0};
    }
}

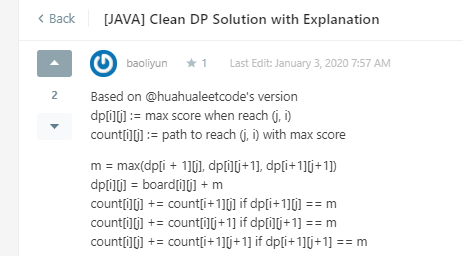
 如果是单纯的最大值，从右下角往上走，每一步选取最大的邻居加上当前值就可以

加上要算path后，当前path必须先判断要从哪个邻居过来（通过判断最大邻居获得）

 https://www.youtube.com/watch?v=WwdjLkWmDPs

这题好叼，两个不同的dp相辅相成。注意最后的判断条件是cc[0][0]>0而不能是dp[0][0] > 0, 否则如果中间有一行xxx的话会出现判断错误