set集合容器使用一种红黑树(Red-Black Tree)的平衡二叉检索树的数据结构,来组织泛华的元素数据。元素数据的检索,使用二叉检索树得中序遍历算法,检索的效率高于vector、deque和list等容器。
红黑树的节点结构:
color left parent right data (颜色 左指针 父指针 右指针 数据域)
红黑树在二叉检索树基础上做的补充定义:(不要求子节点必须是黑色)
1、根节点是黑色
2、其他节点是红色或者黑色
3、每个红色节点的左右节点必须是黑色
4、每条从叶子节点到根节点的路经,都包含相同数目的黑色节点。
注:由性质3,红黑树的任何路经都不会出现两个相邻的红色节点;由性质4,红黑树的所有从根节点到叶子结点的路径中,最长路经不会超过最短路径的2倍。
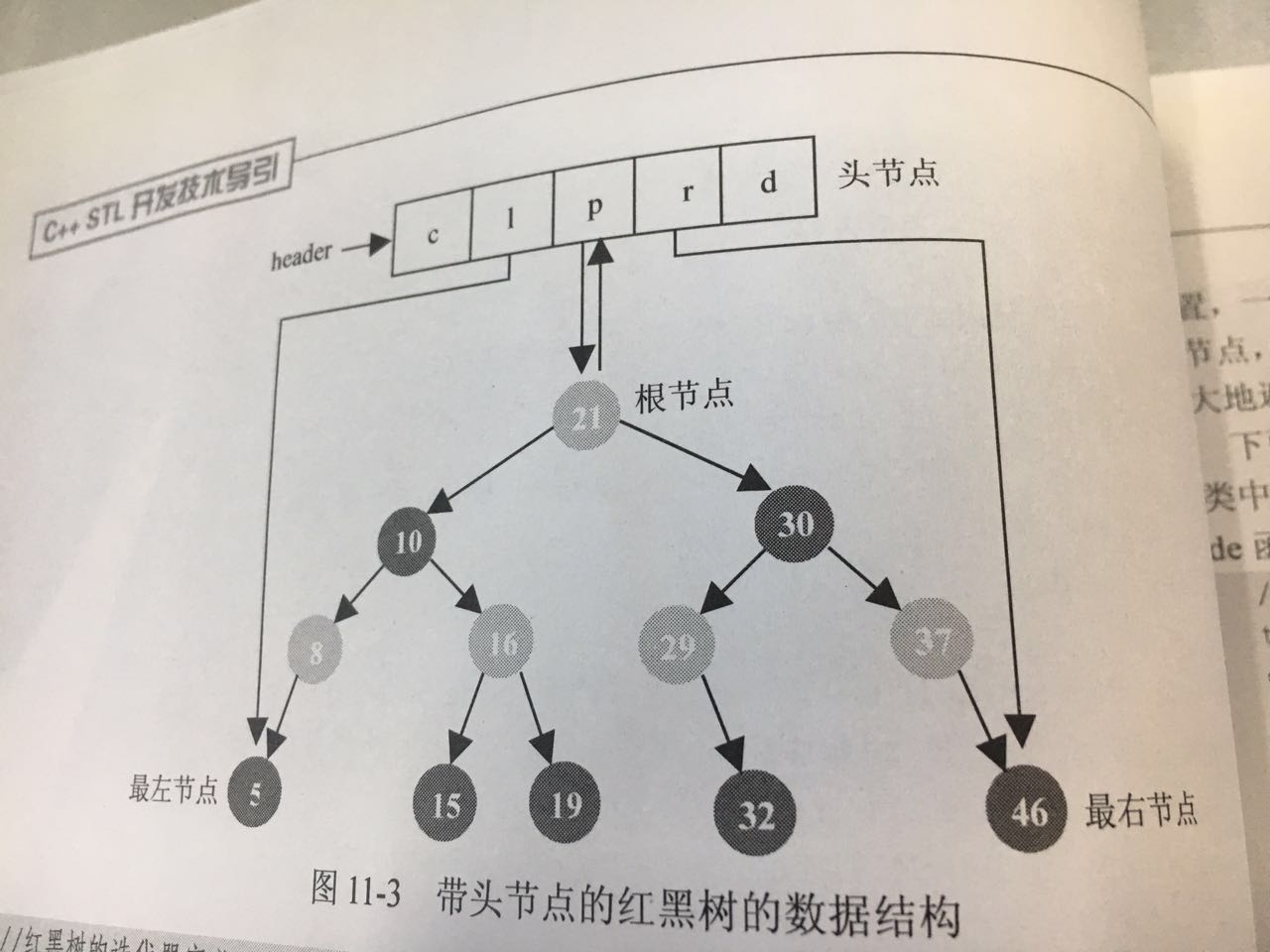
如图,为了提供end函数返回的迭代器,在红黑树的结构上增设了一个头结点,该头结点的位置就是end函数的返回值,即最后一个原色的下一位置。头结点的left指针指向红黑树的最左节点(即键值最小的节点),right指向指针的最右节点(键值最大的节点),parent指针指向红黑树的根节点。头结点为红色。
建树过程:一般是每次插入一个新节点(黑色根节点除外),都着色为红色。然后,再检查红黑树的定义规则是否被破坏,否则要进行子树的左右旋转以作平衡处理。
插入节点:新节点必须先“着色”为红色,因此,当父节点也是红色节点时,所插入的新节点就会破坏原来的红黑树平衡。所以需要从当前插入位置开始上溯到根节点为止,检查是否有父子节点连续出现红色,如果是则进行相应的节点位置调整,使其节点“着色”满足定义要求。
红黑平衡调整函数(Rb_tree_rebalance):
1、当父节点和叔父节点都是红色时,插入节点x,由于x必须是红色,破坏了红黑树的定义要求。因此,可将父节点和叔父节点都改为黑色,祖父节点改为红色,从而使x到其祖父节点符合红黑树的定义。然后继续在祖父节点处往上执行平衡函数循环处理,直至头结点。
2、父节点红色叔父节点黑色时,由于原红黑树平衡,所以祖父节点为黑色。此时,插入节点x,出现冲突。为此现将父节点改为红色,而叔父节点改为红色。但是仍不能满足红黑树路径黑节点数相同的要求,再将x右转,即以x的祖父节点为轴右旋转,从而将黑色节点数维持为原红黑树的平衡数目。
注:其中1、2又分为父节点为左子树和右子树 两种情况。
删除节点:每删除一个节点,也必须要考虑红黑平衡。
注:其中的find函数找所有节点中>=k并且<=k的节点处。
set插入节点调用:insert_unique();
multiset插入调用:insert_equal();
刚看完set数据集,马上来到map映照容器。
map容器元素的数据结构:键值+映照数据
map的元素可通过pair封装成一个结构对象,map容器要做的就是将这个pair对象插入到红黑树,完成一个元素的添加。同时,也要提供一个仅使用键值进行比较的函数对象,传递给红黑树。由此,可利用红黑树操作,将map元素数据插入到二叉树中的正确位置,也可根据键值进行元素的删除的检索。
总结:map跟set的基础数据结构一样,只是在其上增长成为pair,而且map还定义了数组的“【】”操作符,不仅可用键值的方式访问元素的映照数据,还可以用来添加map容器的元素。
multimap:多重映照容器。使用红黑树的insert_equal函数插入元素。允许元素键值的重复插入,使得数组操作符“【】”利用键值访问失去意义,所以multimap并没有定义数组方式的“【】”操作运算。
红黑树插入算法复杂度:查找复杂度:O(lgn)+修复复杂度(O(1),O(lgn))=O(lgn);
红黑树删除算法复杂度:查找复杂度:O(lgn)+修复复杂度(O(1),O(lgn))=O(lgn);