Word2Vec

Word2vec基础

词嵌入的假设，是通过一个词所在的上下文可以获得词的语义甚至语法结构，有相似上下文的词在向量空间中是邻近的点。

背景概念

Word2Vec要解决的根本问题，说到底是自然语言处理的问题。一般认为自然语言处理模型氛围两大派系，分别是形式文法和统计语言模型

统计语言模型

简单地说，可以用统一地形式化表示：

[p(S)=p(w_1,w_2,cdots,w_n)=prodlimits_{i=1}^{n}p(w_i|w_1,w_2,…,w_{i-1}) ]

上述表示可以看做是用来计算词构成一个句子的概率模型，这就是统计语言模型的本质。但是概率的计算是个大问题，数据稀疏、参数过多，很难实际运用。前辈们研究了各种模型。例如n-gram、n-pos、决策树模型、最大熵模型等

n-gram

基于马尔科夫假设，即认为每个词只与前面n−1个词（上下文）有关。例如bigram：

[p(S)=p(w_1)p(w_2|w_1)p(w_3|w_2)…p(w_n|w_{n-1}) ]

至于n的选择，在NLP任务中，普遍认为只需使用2或3，而概率的计算实质为：

[p(w_i|w_1,w_2,cdots,w_{i-1})=frac{count(w_1,w_2,cdots,w_{i-1},w_i)}{count(w_1,w_2,cdots,w_{i-1})} ]

神经网络语言模型(NNLM)

Distributed Representation的代表，每个输入词都是一个实数向量，而模型包含输入层、投影层、隐藏层和输出层。这个直接读Bengio2003的论文《A Neural Probabilistic Language Model》

Log-Bilinear模型

虽然与Word2Vec关系紧密，但与本文话题暂时不相干，所以暂不展开

词向量

具体地，词如何用向量来表示？通常认为有两种基本思路，一种称为One-hot Representation，而另一种叫做Distributed Representation。

One-hot的表示方法，非常稀疏, 每个词就是一个很长的向量，向量的维度就是词表的大小，而只有该词对应位置的数字是1，其他都是0。这种表示方法无法捕捉词与词之间的相似关系，且容易发生维数灾难。

Distributed的表示方法，Hinton在1986年提出，大致思想是用较低维度的实数向量来表示词，而用词之间的距离（例如余弦距离）来表示相似度。普遍认为这种方法能够较好地捕捉词与词之间的语义相似度。

许多模型或方法可以用来获取词向量，除了word2vec使用的模型外，LSA矩阵分解模型、pLSA潜在语义分析模型、LDA文档生成模型，也均可用来估计词向量。

数据结构

Huffman编码

Huffman编码是一种用于无损数据压缩的熵编码（权编码）算法。由大卫·霍夫曼在1952年发明。该方法通过一种变长编码表来对符号进行编码，而变长编码表是通过评估符号出现概率的方法得到，目标是出现概率高的符号使用较短的编码，出现概率低的符号则使用较长的编码。这种方式能有效降低编码之后的字符串的平均长度。

在谈论数据结构的时候，Huffman编码又称为最优二叉树，表示一种带权路径长度最短的二叉树。带权路径长度，指的就是叶子结点的权值乘以该结点到根结点的路径长度。

因此最短长度问题被转化为构建一个由字符（每个字符都是叶子结点）的出现频率作为权值所产生的Huffman树的问题。

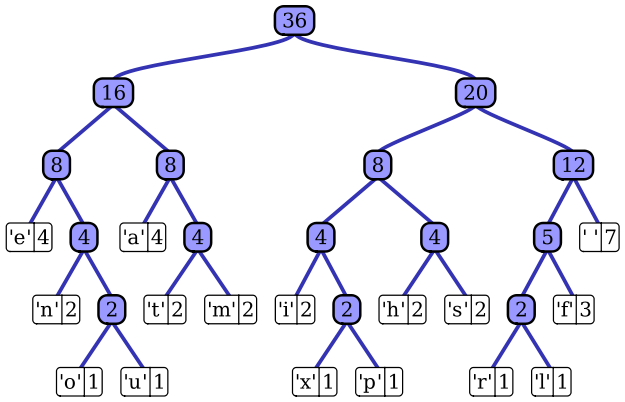
构造Huffman树

算法描述：假设有n个权值，则构造出来的Huffman树有n个叶子结点。若n个权值分别为({w_1,w_2,dots,w_n})

1. 将({w_1,w_2,dots,w_n})当作n棵树（每棵树1个结点）组成的森林
2. 选择根结点权值最小的两棵树，合并，获得一棵新树，且新树的根结点权值为其左、右子树根结点权值之和。词频大的结点作为左孩子结点，词频小的作为右孩子结点
3. 从森林中删除被选中的树，保留新树
4. 重复2、3步，直至森林中只剩下一棵树为止

模型概要

CBOW

CBOW（Continuous Bag-of-Words Model）：在已知上下文，例如(w_{t−2},w_{t−1},w_{t+1},w_{t+2})的前提下，如何预测当前词(w_t)。学习的目标函数是最大化对数似然函数:

[sum limits_{w in C}log p(w|Context(w)) ]

Skip-gram

Skip-gram（Continuous Skip-gram Model）：在已知当前词(w_t)的前提下，预测其上下文，例如(w_{t−2},w_{t−1},w_{t+1},w_{t+2})。目标函数形如:

[sum limits_{w in C}log p(Context(w)|w) ]

模型比较

CBOW和Skip-gram均为三层神经网络（输入层、投影层和输出层），而上下文的词的具体个数是可定义的。窗口大小为5时，两个模型的网络结构如下：

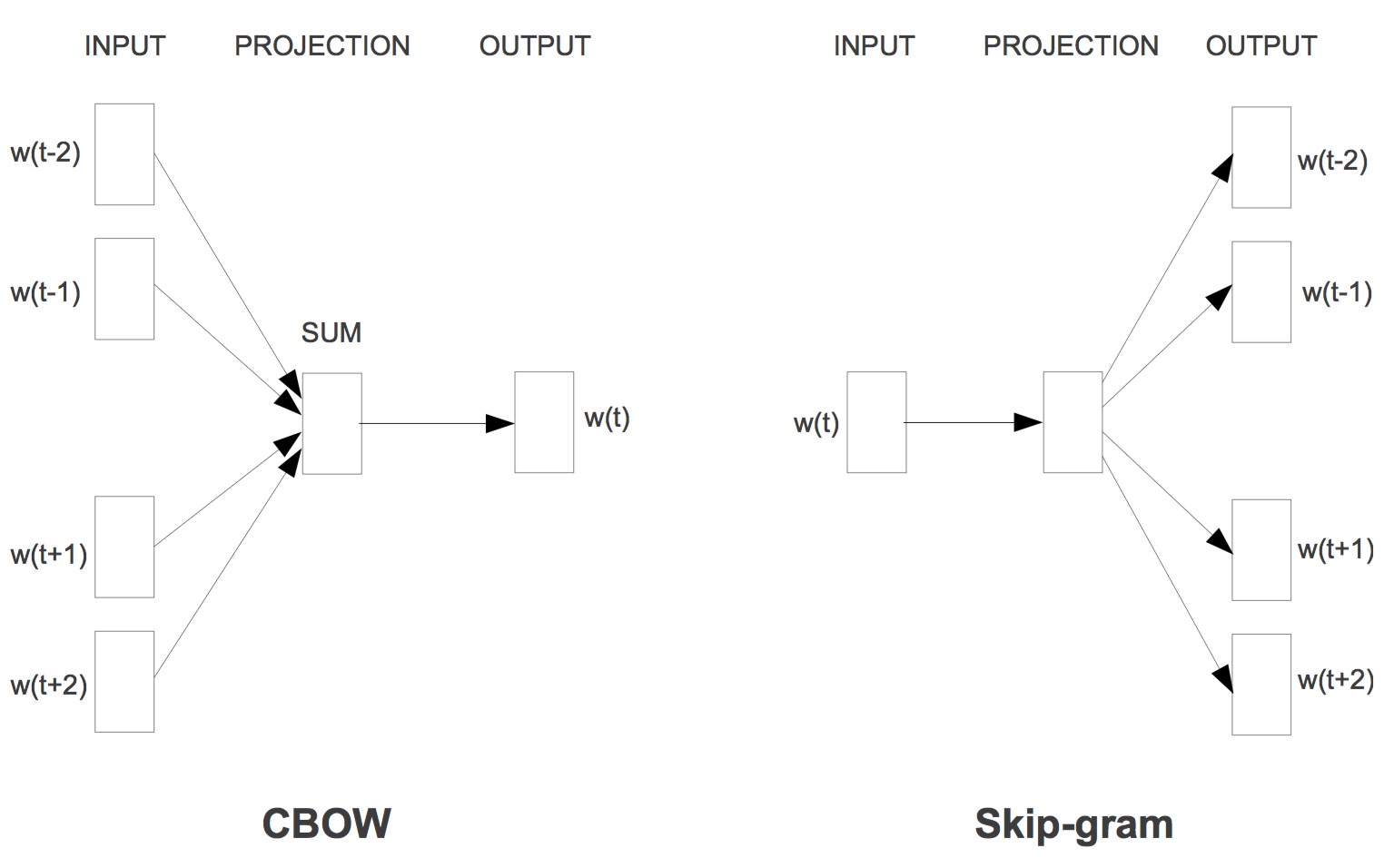
同样用于计算概率值，从模型的计算方式看，skip-gram想要预测更多（上下文），一次会更比CBOW慢一些，但有观点认为对低频词效果更好一些。

算法策略

然而，上面的公式计算很不切实际，因为计算(log p(w_{t+j}|w_t))的梯度与W的大小直接相关。为了降低复杂度，Word2Vec使用了Hierarchical Softmax和Negative Sampling两种求解策略。普遍认为Hierarchical Softmax对低频词效果较好；Negative Sampling对高频词效果较好，向量维度较低时效果更好。

Hierarchical Softmax

作为一种计算高效的近似方法，Hierarchical Softmax被广泛使用。Morin和Bengio首先将这种方法引入神经网络语言模型。该方法不用为了获得概率分布而评估神经网络中的(W)个输出结点，而只需要评估大约(log_2(W))个结点。层次Softmax使用一种二叉树结构来表示词典里的所有词，(V)个词都是二叉树的叶子结点，而这棵树一共有(V−1)个非叶子结点。

对于每个叶子结点（词），总有一条从根结点出发到该结点的唯一路径。这个路径很重要，因为要靠它来估算这个词出现的概率。以下图为例，白色结点为词典中的词，深色是非叶子结点。图中画出了从根结点到词(w_2)的唯一路径，路径长度(L(w_2)=4)，而(n(w,j))表示从根结点到词w2的路径上的的第(j)个结点。

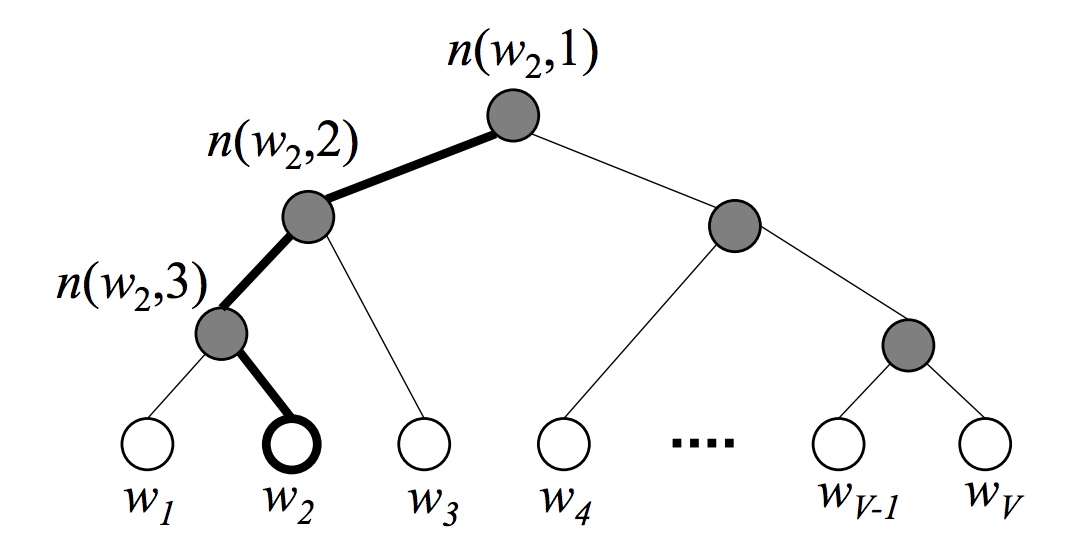
在层次Softmax模型中，叶子节点的词没有直接输出的向量，而非叶子节点其实都有响应的输出向量。

求目标词的概率

在模型的训练过程中，通过Huffman编码，构造了一颗庞大的Huffman树，同时会给非叶子结点赋予向量。我们要计算的是目标词w的概率，这个概率的具体含义，是指从root结点开始随机走，走到目标词w的概率。因此在途中路过非叶子结点（包括root）时，需要分别知道往左走和往右走的概率。例如到达非叶子节点n的时候往左边走和往右边走的概率分别是：

[p(n,left)=sigma( heta_n^Tcdot h) ]

[p(n,right)=1-sigma( heta_n^Tcdot h)=sigma(- heta_n^Tcdot h) ]

以上图中目标词为(w_2)为例:

[egin{aligned} p(w_2)& = p(n(w_2,1),left)cdot p(n(w_2,2),left)cdot p(n(w_2,3),right) \ & = sigma( heta_{n(w_2,1)}^Tcdot h) cdot sigma( heta_{n(w_2,2)}^Tcdot h) cdot sigma( heta_{n(w_2,3)}^Tcdot h) cdot end{aligned}]

到这里可以看出目标词为(w)的概率可以表示为：

[p(w)=prod limits_{j=1}^{L(w)-1} sigma(sign(w,j)cdot heta^T_{n(w,j)}h) ]

其中(θ_{n(w,j)})是非叶子结点(n(w,j))的向量表示（即输出向量）；h是隐藏层的输出值，从输入词的向量中计算得来；(sign(x,j))是一个特殊函数定义：

[egin{aligned} sign(w,j)= egin{cases} 1, quad 若n(w,j+1)是n(w,j)的左孩子 \ -1, quad 若n(w,j+1)是n(w,j)的右孩子 \ end{cases}end{aligned}]

此外，所有词的概率和为1，即：

[sum limits_{i=1}^{n}p(w_i)=1 ]

参数更新公式

[ heta^{(new)}_j= heta^{(old)}_j - eta(sigma( heta_j^T h)-t_j)h ]

其中(j=1,2,cdots,L(w)-1)

Negative Sampling

原文博客

Hierarchical Softmax的另一个替代方法叫做Noise Contrastive Estimation(NCE)，Gutmann和Hyvarinen介绍了这种方法，而Mnih和Teh将该方法应用到了语言模型中。但是如果我们的训练样本里的中心词(w)是一个很生僻的词，那么就得在霍夫曼树中辛苦的向下走很久了。

比如我们有一个训练样本，中心词是(w),它周围上下文共有(2c)个词，记为(context(w))。由于这个中心词(w),的确和(context(w))相关存在，因此它是一个真实的正例。通过Negative Sampling采样，我们得到(neg)个和(w)不同的中心词(w_i,i=1,2,..neg)，这样(context(w))和(w_i)就组成了neg个并不真实存在的负例。利用这一个正例和neg个负例，我们进行二元逻辑回归，得到负采样对应每个词(w_i)对应的模型参数(θ_i)，和每个词的词向量。

从上面的描述可以看出，Negative Sampling由于没有采用霍夫曼树，每次只是通过采样neg个不同的中心词做负例，就可以训练模型，因此整个过程要比Hierarchical Softmax简单。

不过有两个问题还需要弄明白：1）如何通过一个正例和neg个负例进行二元逻辑回归呢？ 2） 如何进行负采样呢？

负采样的方法

现在我们来看看如何进行负采样，得到neg个负例。word2vec采样的方法并不复杂，如果词汇表的大小为V,那么我们就将一段长度为1的线段分成(V)份，每份对应词汇表中的一个词。当然每个词对应的线段长度是不一样的，高频词对应的线段长，低频词对应的线段短。每个词w的线段长度由下式决定:

[len(w)=frac{count(w)}{sum_{uin vocab}count(u)} ]

在word2vec中，分子和分母都取了3/4次幂(调参)如下:

[len(w)=frac{count(w)^{3/4}}{sum_{uin vocab}count(u)^{3/4}} ]

在采样前，我们将这段长度为1的线段划分成M等份，这里(M>>V)，这样可以保证每个词对应的线段都会划分成对应的小块。而M份中的每一份都会落在某一个词对应的线段上。在采样的时候，我们只需要从(M)个位置中采样出neg个位置就行，此时采样到的每一个位置对应到的线段所属的词就是我们的负例词。

在word2vec中，(M)取值默认为(10^8)。(M)足够大，所以每个词被采样到的概率近似于线段的长度。

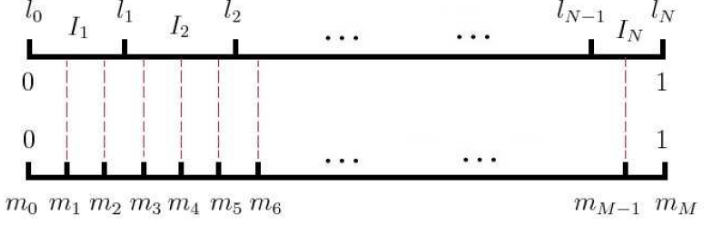
预处理技巧

以下根据源代码来看下两个初始化环节

词典构建

拿到sentences以后首先是创建词典，即从文本序列中创建一个词典。词典数据是一个词对应一个出现次数，词典的规模是可以定义的，有一个参数叫做max_vocab_size即是用来限定最大词典量的。因为这是创建词典的过程，一般希望出现频率较高的词被保留，而频率较低的词被略去。所以统计的过程中，如果当前词汇数超过max_vocab_size，则需要按略去词频低于min_reduce的词，初始化的时候，min_reduce为1。随着实际词典的增大，min_reduce有可能会递增。

SubSampling

全部扫过一遍词典后，需要再次考虑删去总体频率较低的词（出现次数少于min_count的长尾词）。不过，最重要的还是Subsampling。

SubSampling有时候被称作DownSampling，也曾有人译作亚采样，实际是对高频词进行随机采样，关于随机采样的选择问题，考虑高频词往往提供相对较少的信息，因此可以将高于特定词频的词语丢弃掉，以提高训练速度。Mikolov在论文指出这种亚采样能够带来2到10倍的性能提升，并能够提升低频词的表示精度。

采样参数sample表示采样百分比，默认是1e-3，Google推荐的是1e-3至1e-5。

[p(w_i)=1-sqrt{frac{t}{f(w_i)}} ]

其中(f(w_i))是词(w_i)的词频，t是阈值。而这个是Mikolov论文里的说法，实际Word2Vec的代码，以及后续gensim的实现，都采用了如下公式来表示词(w_i)被丢弃的概率：

[p(w_i)=1-()sqrt{frac{v_{wi}}{sample*N_w}+1}*frac{sample*N_w}{v_{wi}} ]

其中：(N_W)是参与训练的单词总数，包含重复单词，实质即词频累加；(v_{wi})是词(w_i)的词频。在gensim的实现中，对(sample<1)和(sample geq 1)的情况区分对待，具体可去看gensim版源码。

Word2vec模型细节

原文博客

CBOW

One-word context

从CBOW模型的最简单版本开始介绍——One-word context。即假定context（预测目标单词的上下文信息）只有一个单词，也就是说One-word context 模型是在只要一个上下文单词（one context word）的情况下来预测一个目标单词（one target word）的生成概率

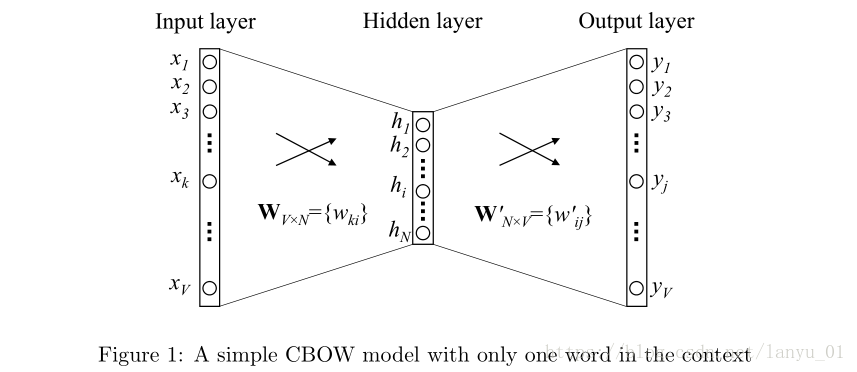
如图描述的就是One-word context定义之下的神经网络模型。这里我们假设文本词汇量的大小为(V),隐藏层的大小为(N)，相邻层的神经元是全连接的。输入层是一个用one-hot方式编码的单词向量(x=(x_1,...,x_V))，其中只有一个(x_i)为1，其余均为0。 从输入层到 隐藏层的权重值可以用一个(V imes N)维的矩阵(W)来表示:

[egin{bmatrix} w_{11} & w_{12} & cdots & w_{1N} \ cdots & cdots & cdots & cdots \ w_{V1} & w_{V2} & cdots & w_{VN} end{bmatrix}]

其中(W)矩阵的每一行代表的是一个与输入层相关的单词的(N)维向量表示形式(v_ω)。那么假设我们给定了一个输入单词（a context）,其单词向量的第(k)个元素(x_k=1)，其余均为0，则有

[h=W^Tx=W^T_{k,cdot}x_k=v^T_{wI} ]

从上式我们可以看出，(h)向量完全是从(W)矩阵第(k)行复制过来的,(v_{ωi})即为输入单词(ω_I)(上下文单词)的一种向量表示

分析完输入层到隐藏层之后，我们再看隐藏层到输出层，同样连接权重用一个新的
(N imes V)矩阵(W^{'}={ω^{'}_{ij}})来表示如下:

[egin{bmatrix} w^{'}_{11} & w^{'}_{12} & cdots & w^{'}_{1V} \ cdots & cdots & cdots & cdots \ w^{'}_{N1} & w^{'}_{N2} & cdots & w^{'}_{NV} end{bmatrix}]

通过这些权重，我们可以为词表中的每一个单词都计算出一个得分(mu_j):

[mu_j=(v^{'}_{wj})^Th ]

其中(v^{'}_{wj})即为矩阵(W^{'})的第(j)列向量

经过以上讨论之后，我们可以使用一种对数-线性分类模型softmax函数来计算单词的后验分布（是多项式分布）

[p(w_j|w_I)=y_j=frac{exp(mu_j)}{sum_{j=1}^{V}exp(mu_j)} ]

其中，(y_j)表示输出层第(j)个神经元的输出。结合上面三式，有训练目标：

[p(w_j|w_I)=frac{exp((v^{'}_{wj})^Tv_{wI})}{sum_{j=1}^{V}exp((v^{'}_{wj})^Tv_{wI})} ]

(v_ω)和(v^{′}_ω)是单词的两种向量表示形式。其中(v_ω)实际上是权重矩阵(W)（input->hidden）的某一行向量，(v^{′}_ω)则是权重矩阵(W^{′})（hidden->output）的某一列向量。分别称为“输入向量和“输出向量”

Multi-word context

基于multi-word context的CBOW模型就是利用多个上下文单词来推测中心单词target word的一种模型

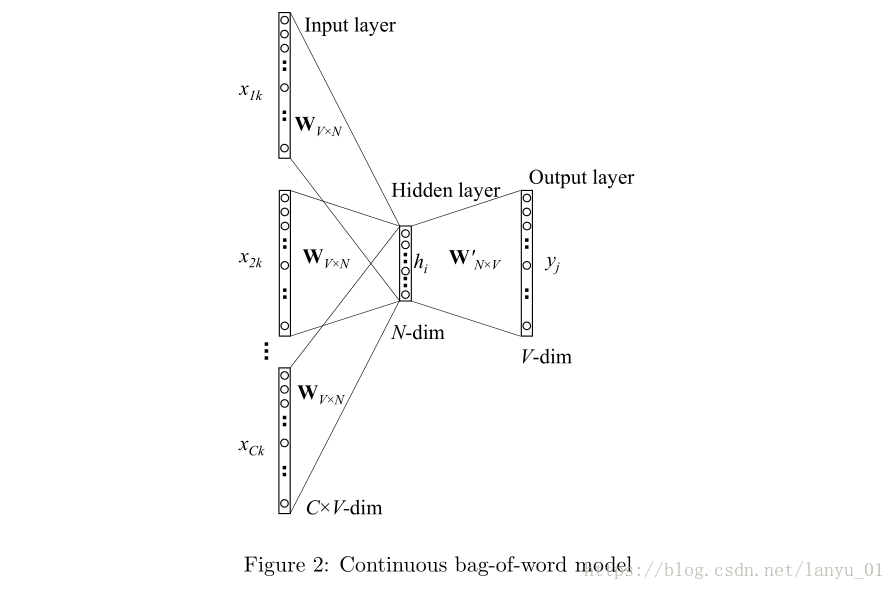
其隐藏层的输出值的计算过程为：首先将输入的上下文单词（context words）的向量叠加起来并取其平均值，接着与input→hidden的权重矩阵相乘，作为最终的结果，公式如下:

[egin{aligned} h & = dfrac{1}{C}W^T(x_1+x_2+cdots+x_C) \ & = dfrac{1}{C}(v_{w1}+v_{w2}+cdots+x_{wC})^T end{aligned}]

其中(C)为上下文单词的个数，(ω_1,dots,ω_C)为上下文单词，(v_ω)为单词(ω)的输入向量。损失函数为：

[egin{aligned} mathcal{L} & = -log p(w_O|w_{I,1},w_{I,2},cdots,w_{I,C}) \ & = -mu^*_j+log sum limits_{j=1}^V exp(mu_j^{'}) \ & = -(v^{'}_{wO})^Tcdot h + log sum limits_{j=1}^Vexp ((v^{'}_{wj})^Tcdot h) end{aligned}]

Skip-gram

与CBOW模型正好相反，Skip-Gram模型是根据中心单词（target word）来预测其上上下文信息（context words）

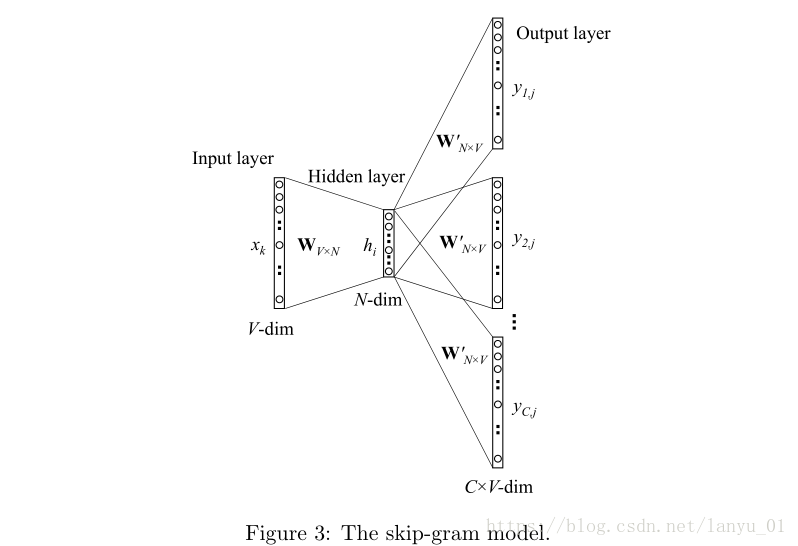
我们仍然使用(v_{ωI})来表示输入层上唯一的那个单词的输入向量，因此，我们对于隐藏层的输出值(h)的计算公式与第一节公式相同，表示如下:

[h=W^T_{k,cdot}:=v_{wI} ]

上式显示，(h)向量其实就是input->hidden权重矩阵(W)的某一行结合输入单词(ω_I)的向量拷贝。在输出层，与CBOW模型的输出为单个多项式分布不同的是，SG模型在输出层输出了C个多项式分布。每个输出都使用相同的hidden->output矩阵计算：

[p(w_{c,j}=w_{O,c}|w_I)=y_{c,j}=frac{exp(mu_{c,j})}{sum_{j=1}^{V}exp(mu_{j}^{'})} ]

其中，(ω_{c,j})表示输出层的第(c)个panel的第(j)个单词（何为panel?就是输出层的表示每个上下文单词的神经元的组合，图中一种有C个context words，所以总共有C个panel）；(ω_{O,c})实际上表示的是输出上下文单词（output context words）的第(c)个单词；(ω_I)是唯一的输入单词；(y_{c,j})为输出层的第c个panel上的第j个神经单元的概率输出值；(mu_{c,j})表示的是输出层第c个panel的第j个神经元的输入值；由于输出层的所有panels共享同一权重矩阵(W^{′}),因此：

[mu_{c,j}=mu_j=(v_{wj}^{'})^T cdot h quad ext{for} c=1,2,cdots,C ]

其中，(v_{wj}^{'})为词汇表第(j)个单词(ω_j)的输出向量；同样，它也是取自于hidden→output权重矩阵(W^{′})的一列