二叉查找树
一颗查找树是这样一颗树,其元素的组织方式能让我们方便地找到一个具体的元素,查找树中的元素按照它们之间相对关系的特定方式来保存。
- 二叉查找树是一棵二叉树,对其中的每个节点,左子树上的元素小于父节点的值,而右子树上的元素大于等于父节点的值。
- 二叉查找树可以保存任意的数据类型或对象,只要有办法能判断它们之间的大小,可以使用compareTo方法,所有实现Comparable接口的对象都可以保存的二叉查找树中。
添加元素
- 若树为空,则添加的元素作为树的根
- 若树不为空,则比较元素与根节点,若大于根节点则转入比较左子树的根节点,若小于根节点则转入比较右子树的根节点,根据上述规则进行递归,直到某个子树的左右子树为空,则将该元素作为其左右节点,特别的相等的值保存在右子树中
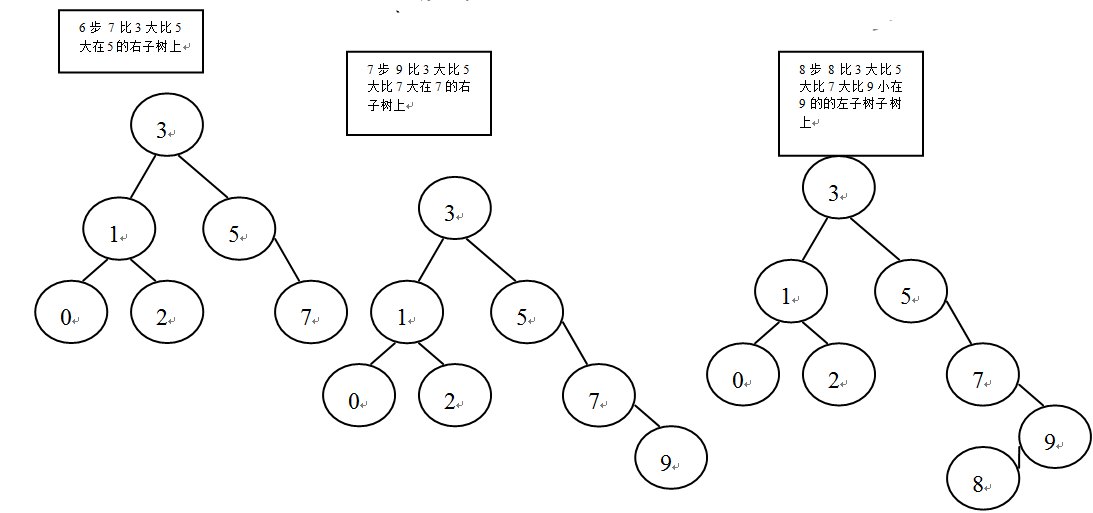
删除元素
- 情况一:要删除的元素结点是叶子结点,只需要修改它的双亲结点的指针为空
- 情况二:要删除的元素节点仅有一个子节点,只需要用子节点来取代被删的父节点。
- 情况三:要删除的节点有两个子节点。要删除有两个子节点的节点时,先从树中删除它的中序后继,然后用这个中序后继来替代实际要被删除的节点,被删除元素的子节点变为代替节点的子节点。
//BSTNode
public BSTNode<T> remove(T target)
{
BSTNode<T> result = this;
if (target.compareTo(element) == 0)
{
if (left == null && right == null)
result = null;
else if (left != null && right == null)
result = (BSTNode)left;
else if (left == null && right != null)
result = (BSTNode)right;
else
{
result = getSuccessor();
result.left = left;
result.right = right;
}
}
else
if (target.compareTo(element) < 0)
if (left != null)
left = ((BSTNode)left).remove(target);
else
if (right != null)
right = ((BSTNode)right).remove(target);
return result;
}
// LInkenBinarySearchTree
public T remove (T target)
{
BSTNode<T> node = null;
if (root != null)
node = ((BSTNode)root).find(target);
if (node == null)
throw new ElementNotFoundException ("Remove operation failed. "
+ "No such element in tree.");
root = ((BSTNode)root).remove(target);
return node.getElement();
}
protected BSTNode<T> getSuccessor()
{
BSTNode<T> successor = (BSTNode)right;
while (successor.getLeft() != null)
successor = (BSTNode) successor.getLeft();
((BSTNode)right).remove (successor.getElement());
return successor;
}
-
首先在LinkedBinarySearchTree中remove方法调用乐方法find用来找到目标元素,返回值是被删除的值,而当被删除的树为空或者没有找到目标元素时,则抛出异常。找到元素后则调用BSTNode的remove方法删除指定元素。可以看到BSTNode的remove方法有很多if判断方法。外层if语句用来判断删除元素是否与根元素相等。若相等:内层有四个if语句代表前面提到的三种情况。其中最复杂的是第三种情况:如果存在两个子节点,先调用getSuccessor方法从代码中可以读出她返回指向被删节点的中序后继引用(如何找到中序后继:从节点开始向右走一步
BSTNode<T> successor = (BSTNode)right;,然后一直向左走知道左节点为空while (successor.getLeft() != null) successor = (BSTNode) successor.getLeft();,最后调用remove方法删除这个后继节点。 -
图例:删除途中30
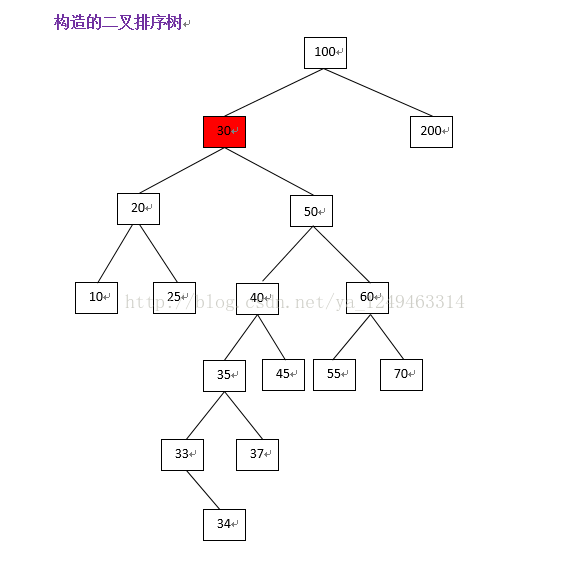
删除节点30后的树图
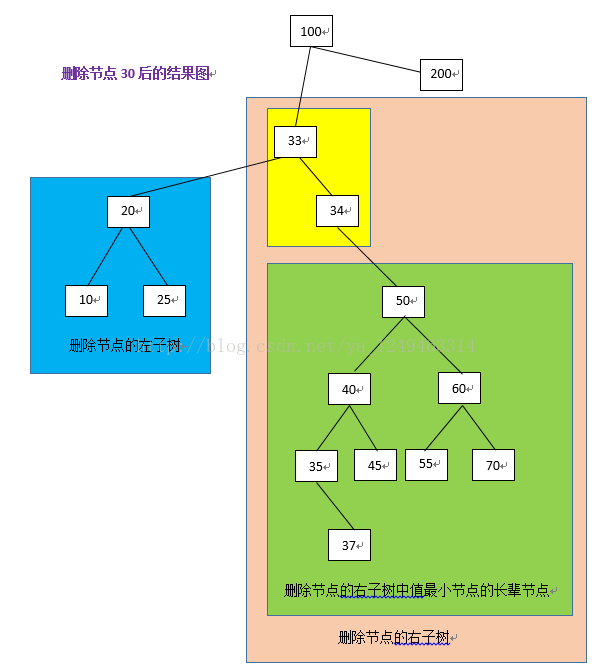
-
若不相等:首先判断目标元素与根元素的大小,若大于则转入根元素的左节点进行递归,若小于则转入根元素的右节点进行递归。
平衡二叉查找树
右旋转
- 令根的左子结点变为新的根
- 令原根结点变为新的根结点的右子结点
- 令原根的左子结点的右子结点变为原根结点的新的左子节点。
左旋转
- 令根的右子结点变为新的根
- 令原根结点变为新根节点的左子节点
- 令原根的右子结点的左子结点县委原根结点的新右子结点