题目背景
在下克上异变中,博丽灵梦为了找到异变的源头,一路打到了天守阁
异变主谋鬼人正邪为了迎击,将天守阁反复颠倒过来,而年久失修的天守阁也因此掉下了很多块地板
异变结束后,恢复了正常大小的小碗回到了天守阁,想要修复这里的地板,她需要知道自己要采购的地板数量(一个惊人的数字),于是,她找到了精通oi的你来帮忙
题目描述
为了使万宝槌能发挥出全部魔力,小碗会将买来的地板铺满一个任意边长的正方形(地板有图案,因此不允许旋转,当然,地板不允许重叠)来达到最大共鸣
现在,她能够买到规格为a∗b的地板,为了省钱,她会购买尽可能数量少的地板
现在,她想知道对于每一对a,b(1≤a,b≤n),她最少需要购买的地板数量
由于输出可能很大,所以你只需要输出所有答案的乘积即可,为了避免高精度,小碗很良心的让你将答案对19260817取模
输入输出格式
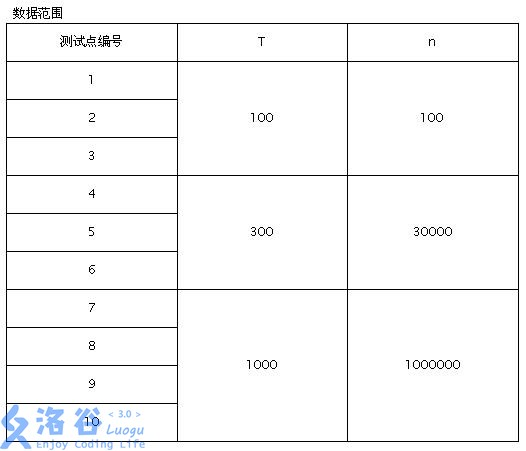
输入格式:第一行一个整数T,表示数据组数
下面T行,每行一个整数n
共T行,每行一个整数,表示取模后的答案
输入输出样例
说明
样例解释:
对于n=1,a,b仅有(1,1)一种情况,只需要一块1∗1的地板,答案为1
对于n=2,a,b有(1,1),(1,2),(2,1),(2,2)四种情况,分别需要一块(1*1),两块(1∗2),两块(2∗1),一块(2∗2)的地板,答案为1∗2∗2∗1=4
追加解释:a,b有四种取值,分别是(1,1),(1,2),(2,1),(2,2)
当只能买到1∗1的地板时,需要一块(本身就是正方形)
当只能买到1∗2的地板时,需要两块(两块拼在一起组成2∗2的正方形)
当只能买到2∗1的地板时,需要两块(两块拼在一起组成2∗2的正方形)
当只能买到2∗2的地板时,需要一块(本身就是正方形)
答案就是这些数的乘积,即4
第一天停课的早上,在$yuli$dalao已经a掉12道题的同时,终于把这道题搞清楚了。
出题人颠覆了我对noip的看法!

抱头痛哭QAQ
题解写的确实清楚,但这这这noipd2t1考的知识点要不要太多aaa!!!欧拉函数+逆元线性筛,$gcd$和$lcm$相关公式推导,同除$O(sqrt{n})$优化.....我大概也就到了能把第一步式子推出来的地步吧....
先考虑单个询问的情况,可以得到如下结论:
用$a*b$规格的地板摆成的正方形的边长最小是$lcm(a,b)$(木板不允许旋转),所以需要最小的木板数量是$frac{lcm(a,b)}{a}*frac{lcm(a,b)}{b}$
问题中说要把所有可能的$(a,b)$的答案求乘积,那么问题就转换成了求
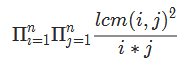
首先你必须知道
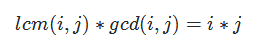
(唯一分解后易证)
因此
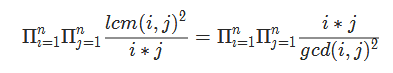
先考虑分子:
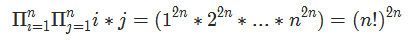
所以可以先$O(n)$预处理出阶乘$fac(i)$,用快速幂$O(logn)$算出分子
接下来考虑分母
为了方便,可以先求出
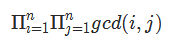
再平方
考虑枚举$d$,那么我们求出对于每个$d$有多少对$(i,j)$满足$gcd(i,j)=d$再套用快速幂即可
显然$i,j$都是$d$的倍数是必要条件,所以设$i=k_1d,j=k_2d(k1,k2≤lfloor frac{n}{d}
floor)$
那么当且仅当$gcd(k1,k2)=1$即$k1,k2$互质时符合$gcd(i,j)=d$的条件(否则$gcd$可以扩大为$d*gcd(k1,k2)$
不妨令 $k1>k2$,那么符合条件的点对数 为每个在范围内的$k1$,小于它且与它互质的数的个数的和(即$sumφ$),所以真正的答案就是
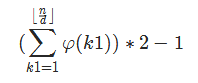
好了,到现在复杂度为$O(n+Tnlogn)$,可以拿到$60$分的好成绩(雾)
最后一个优化:
不难发现,$lfloor frac{n}{d}
floor$的取值只有$2sqrt{n}$种,那么可以把$lfloor frac{n}{d}
floor$相等的所有d放在一起处理
假设某一段从i到j的所有数的这个值都等于x,那么这一段的乘积就等于
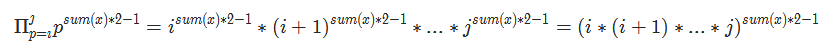
那么先预处理出$19260817$的逆元$inv(i)$,这一段的答案就是$(fac(j)*inv(fac(i-1)))^{sum(x)*2-1}$
这样处理后的最终复杂度是$O(n+Tsqrt{n}log(n))$,可以愉快的通过此题
#include<bits/stdc++.h> #define LL long long #define mod 19260817 #define maxn 1000000 using namespace std; LL mpow(LL a, LL b) { LL ans = 1; for(; b; b >>= 1, a = a * a % mod) if(b & 1) ans = ans * a % mod; return ans; } int isnot[maxn+5], prime[maxn+5], t; int fac[maxn+5], inv[mod+5]; LL phi[maxn+5]; void init() { isnot[1] = 1; phi[1] = 1; for(int i = 2; i <= maxn; i ++) { if(!isnot[i]) { prime[++t] = i; phi[i] = i - 1; } for(int j = 1; j <= t; j ++) { if(i * prime[j] > maxn) break; isnot[i * prime[j]] = 1; if(i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j] - 1); else { phi[i * prime[j]] = phi[i] * prime[j]; break; } } } for(LL i = 2; i <= maxn; i ++) phi[i] += phi[i-1]; fac[0] = 1; for(LL i = 1; i <= maxn; i ++) fac[i] = (LL)(fac[i-1] * i) % mod; inv[0] = inv[1] = 1; for(LL i = 2; i < mod; i ++) inv[i] = (LL)((LL)(-(mod / i) * (LL)inv[mod % i]) % mod + mod) % mod; } int main() { int T; scanf("%d", &T); init(); while(T --) { int n; scanf("%d", &n); LL ans1 = mpow(fac[n], 2 * n); LL ans2 = 1; for(LL d = 1, L; d <= n; d = L + 1) { LL p = (LL)2 * phi[n/d] - 1; L = n / (n / d);///////////////////////////////同除优化 ans2 = (LL)ans2 * mpow((LL)fac[L] * (LL)inv[fac[d-1]] % mod, p) % mod; } ans2 = ans2 * ans2 % mod; ans2 = inv[ans2]; printf("%lld ", ans1 * ans2 % mod); } return 0; }
!!!愉快个猪皮怪物!!(不过好在复习了线性筛和一些小公式)
还有一个知识点在这里用到。
BZOJ2818:
2818: Gcd
Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 8803 Solved: 3908
[Submit][Status][Discuss]
Description
给定整数N,求1<=x,y<=N且Gcd(x,y)为素数的
数对(x,y)有多少对.
Input
一个整数N
Output
如题
Sample Input
Sample Output
HINT
hint
对于样例(2,2),(2,4),(3,3),(4,2)
1<=N<=10^7
Source
上面题解也有讲到,设$gcd(x,y)=d$,那么题目就是求对于每个$d$,$gcd(frac{x}{d},frac{y}{d})=1$的对数。设$frac{y}{d}=k1>frac{x}{d}=k2$,我们求$φ$的前缀和,那么就是求$φ(k1)*2-1$($1$会多一个重复)(对于$k1=lfloor frac{n}{d} floor$),然后枚举$d$就可以了。
这道题要求$d$是素数,所以枚举素数就行了。
#include<bits/stdc++.h> #define LL long long #define maxn 10000000 + 5 using namespace std; LL phi[maxn]; int isnot[maxn], prime[maxn], n, t; void init() { isnot[1] = 1; phi[1] = 1; for(int i = 2; i <= n; i ++) { if(!isnot[i]) prime[++t] = i, phi[i] = i - 1; for(int j = 1; j <= t; j ++) { int to = prime[j] * i; if(to > n) break; isnot[to] = 1; if(i % prime[j] == 0) { phi[to] = phi[i] * prime[j];//////////记住就好! break; } else phi[to] = phi[i] * (prime[j] - 1);//////互质用积性函数的性质 } } for(int i = 1; i <= n; i ++) phi[i] += phi[i-1]; } int main() { scanf("%d", &n); init(); LL ans = 0; for(int i = 1; i <= t && prime[i] <= n; i ++) ans += (phi[n/prime[i]] * 2 - 1); printf("%lld", ans); return 0; }