Louvain
Introduce
Louvain算法是社区发现领域中经典的基于模块度最优化的方法,且是目前市场上最常用的社区发现算法。社区发现旨在发现图结构中存在的类簇(而非传统的向量空间)。
Algorithm Theory
-
模块度(modularity)
要想理解Louvain算法需先理解模块度,模块度是衡量一个网络社区划分好坏的度量指标,可以简单理解为“给定算法得到的图中的社区划分D,社区内节点的连边权重和与对应随机图中的连边权重和的差,可以理解为社区内边权重之于社区间边权重的比例,当然,社区内边权重越大,则模块度越大,社区中节点联系更加紧密,社区划分质量越好。”模块度的公式如下所示:

以下均无向无权图为例,m为图中的边数,2m为图的总度数,A为邻接矩阵,当两个节点直接相连时Aij=1,否则Aij=0,ki为节点i的度,δ(ci,cj)为指示函数,当节点i、j位于同一个社区,其为1,否则为0。
公式中比较难理解的是中括号中的第二项,啥意思呢? 之前提到随机图,这边公式中的第二项指的是随机图中度为ki和度为kj的两个节点相连的概率。得到的社区划分与随机图(无规律,且无明显社区结构)相差越大,则社区内连接越紧密,社区间连接越稀疏(即社区边界更明显),发现的社区质量越好。
好了,模块度就理解到这儿,简单总结一下,模块度范围在[-0.5,1),一般模块度越高,发现的社区质量越好。(原始模块度论文表示当模块度值在0.3~0.7之间时,社区质量好)
-
Louvain Flow Chart:
现在进入正题,Louvain算法的总体框架(流程图)如下图所示:
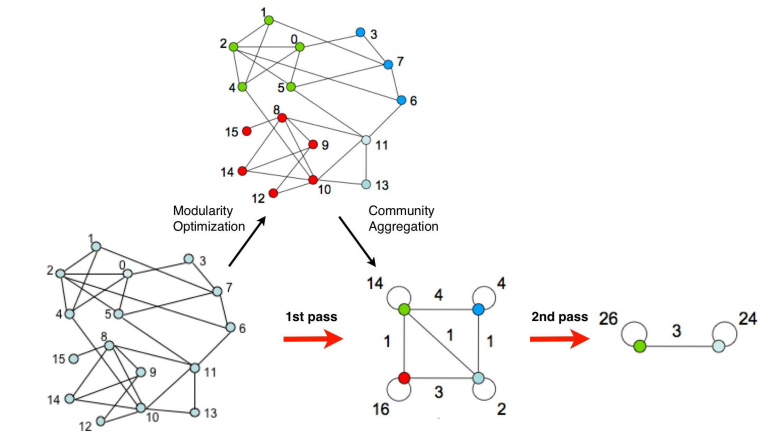
Louvain是一个迭代更新算法(初始每个节点自成一个社区),每个迭代称为一个pass,每个pass都包括两个步骤。即Louvain算法等价于不断迭代以下两个步骤(阶段):
(1)步骤1:首先,为每个节点分配一个单独的社区。其次对于每个节点i,考虑其邻居j,计算将节点i归入节点j所在社区模块度的增益。考虑节点i的所有邻居,并且将节点i归入到模块度增益的社区最大。如果节点i归到他邻居所在社区都没有模块度增益(即模块度增益为0或者负数)的话,那节点i仍然留在他原始的社区中。这个过程反复做,直到改变任何节点的社区标签都没有更进一步的模块度增益就停止,停止之后第一阶段就结束了。以上最重要的就是要搞懂模块度增益这玩意怎么算呢? 模块度增益可以通过以下公式计算。
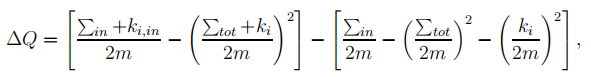
啥意思呢?我们可以化简一下得到如下式子:
Delta Q =[frac{k_{i,in}}{2m}-frac{sum_{tot}k_i}{2m^2}]括号中第一项的意思可以理解为节点i加入邻居所在社区之后对应社区内的连边数。括号中第二项的意思可以理解为结点加入邻居社区后,对应社区间以及社区内的连边数。最大化该模块度增益,就是最大化这个差,这个差大了,就说明节点i加入到这个邻居社区之后,使得该社区的内聚度更高了,社区结构越明显了。emmm,模块度增益最大化大概就是这么个意思了。
(2)步骤2:算法的第二阶段做的事情是,结合步骤1得到的初始社区划分建立一个新的网络,新网络的节点是在第一阶段发现的初始社区(把社区粗化成一个粗化节点),两个粗化节点之间的边由两个社区原始对应的社区间边的权重和(无向图即两个社区间相连的边数),同一社区节点之间的连边权重生成这个社区粗化节点的一个自环边。一旦完成了第二阶段,就将构成的新的网络输入第一阶段再进行迭代(因为粗化(层次的概念),每次网络中的初始社区数会变小,因此后面迭代的速度会更快)。
至此,Louvain算法介绍结束。
Reference
- Blondel V D, Guillaume J L, Lambiotte R, et al. Fast unfolding of communities in large networks[J]. Journal of statistical mechanics: theory and experiment, 2008, 2008(10): P10008.
- 社区发现算法——louvain完全解读
- 模块度与Louvain社区发现算法