为什么使用交叉熵作为损失函数？

如果概括性地回答这个问题，我们其实是希望得到最大似然(maximum likelihood)，使得模型的预测分布与数据的实际分布尽可能相近。而最大化log似然等同于最小化负log似然，最小化负log似然等价于最小化KL散度(相对熵)，KL散度里包含有只与数据集相关而与模型无关的$log{\hat{p}}_{data}$，这一部分对每个特定数据集来说是一个定值，为了简化去掉该部分我们最后得到了交叉熵。

上面博主补充这段如果你不是很理解，可以参见下面来自知乎这张图：

图中：$p(x)$是由数据决定的概率，那么$p(x)$是定值，则它的log $lnp(x)$也是定值，所以最小化交叉熵最终等效与最小化$-\int lnq(x)$，而$-\int lnq(x)$即为负log似然。

也就是说，虽然最小化的是交叉熵，但其实我们的目的是最大似然，因为最大似然有以下性质：

 
最大似然有两个非常好的统计性质：

1. 样本数量趋于无穷大时，模型收敛的概率会随着样本数m的增大而增大。这被称为一致性。
2. 一个一致性估计器能够在固定数目的样本m下取得更低的泛化误差(generalization error)，或者等价的，需要更少的样本就可以得到固定水平的泛化误差。这被称作统计高效性。

最大化log似然和最小化均方误差(MSE)，得到的估计是相同的。



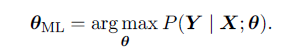
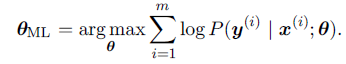
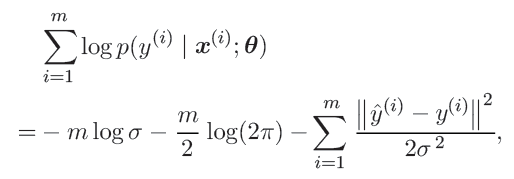
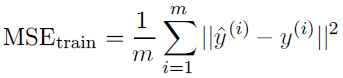
The Cramér-Rao lower bound (Rao, 1945; Cramér, 1946)证明了没有任何其他的一致性估计器(consistent estimator)比最大log似然估计器有更小的MSE。

另外，在梯度计算层面上，交叉熵对参数的偏导不含对sigmoid函数的求导，而均方误差(MSE)等其他则含有sigmoid函数的偏导项。大家知道sigmoid的值很小或者很大时梯度几乎为零，这会使得梯度下降算法无法取得有效进展，交叉熵则避免了这一问题。

综上所述，最小化交叉熵能得到拥有一致性和统计高效性的最大似然，而且在计算上也比其他损失函数要适合优化算法，因此我们通常选择交叉熵作为损失函数。

参考文献

【1】Deep Learning 英文版
【2】https://blog.csdn.net/huwenxing0801/article/details/82791879