软件工程(2018)第3次作业

一、题目

• 最大连续子数组和（最大子段和）

---

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》
二、代码

算法代码借鉴[五种求解最大连续子数组的算法]（https://www.cnblogs.com/AlgrithmsRookie/p/5882379.html）

 #include"stdio.h"
 #include"iostream"
using namespace std;
int sum = 0;
int main()
{
	int length, a[100];
	int i;
	int max_sum(int length, int a[]);
	printf("给定整数的个数:
");
	cin >> length;
	printf("输入数列
");
	for (i = 0; i<length; i++)
	{
		cin >> a[i];
	}
	printf("序列子段和的最大值:
");
	sum = max_sum(length, a);
	printf("%d
", sum);
	return 0;
}
 int max_sum(int length, int a[])
 {
	int b[100];
	b[0] = a[0];
	int max;
	max = b[0];
	for (int i = 1; i<length; i++)
	{
		if (b[i - 1]>0)
			b[i] = b[i - 1] + a[i];
		else
			b[i] = a[i];
		if (b[i]>max)
			max = b[i];
		if (max <= 0)
			max = 0;
	}
	sum = max;
        return sum;
 }

其算法的时间复杂度为O(n)
代码已上传coding.net

三、单元测试选择：五种覆盖标准对比

语句覆盖 每条语句至少执行一次
判定覆盖 判定的每个分支至少执行一次
条件覆盖 判定的每个条件应取到各种可能的值
判定-条件覆盖 同时满足判定覆盖和条件覆盖
条件组合覆盖 判定中各种条件的每一种组合至少出现一次

• 上述程序代码流程图

---

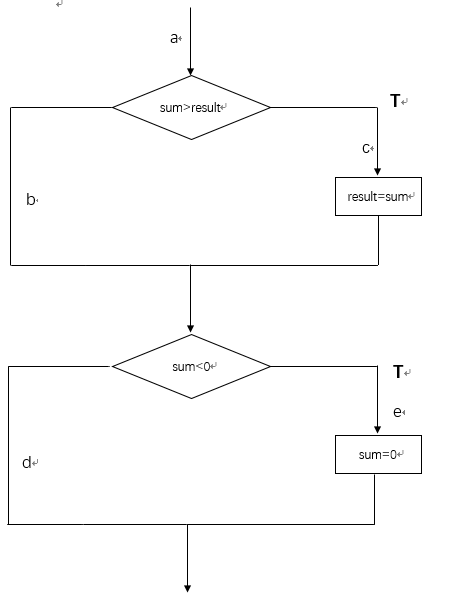
• 故，我选择条件组合覆盖，根据条件组合覆盖的定义，每个判定包含一个条件
  测试用例（-2，11，-4，13，-5）测试结果：20
  测试用例（-1，-3，-5，-6，-2）测试结果：0
  四、测试代码
  ===========
  ···

  TEST_CLASS(UnitTest1)
  {
  public:

   TEST_METHOD(TestMethod1)
   {
   	// TODO: 在此输入测试代码
   	int a[5] = { -1,-3,-5,-7,-9 };
   	int sum = max_sum(6, a);
   	Assert::AreEqual(0, sum);
   }
   TEST_METHOD(TestMethod2)
   {
   	// TODO: 在此输入测试代码
   	int a[5] = { -2,11,-4,,13,-5 };
   	int sum = qiusum(6, a);
   	Assert::AreEqual(30, sum);
   }
  

···
五、总结

这次作业真的是又一次凝练了我的编程能力，收获很多，也发现了很多不足的地方，需要加倍努力才是。