hdu 5128 The E-pang Palace

E-pang Palace was built in Qin dynasty by Emperor Qin Shihuang in Xianyang, Shanxi Province. It was the largest palace ever built by human. It was so large and so magnificent that after many years of construction, it still was not completed. Building the great wall, E-pang Palace and Qin Shihuang's tomb cost so much labor and human lives that people rose to fight against Qin Shihuang's regime. 

Xiang Yu and Liu Bang were two rebel leaders at that time. Liu Bang captured Xianyang -- the capital of Qin. Xiang Yu was very angry about this, and he commanded his army to march to Xianyang. Xiang Yu was the bravest and the strongest warrior at that time, and his army was much more than Liu Bang's. So Liu Bang was frighten and retreated from Xianyang, leaving all treasures in the grand E-pang Palace untouched. When Xiang Yu took Xianyang, he burned E-pang Palce. The fire lasted for more than three months, renouncing the end of Qin dynasty. 

Several years later, Liu Bang defeated Xiangyu and became the first emperor of Han dynasty. He went back to E-pang Palace but saw only some pillars left. Zhang Liang and Xiao He were Liu Bang's two most important ministers, so Liu Bang wanted to give them some awards. Liu Bang told them: "You guys can make two rectangular fences in E-pang Palace, then the land inside the fences will belongs to you. But the corners of the rectangles must be the pillars left on the ground, and two fences can't cross or touch each other." 

To simplify the problem, E-pang Palace can be consider as a plane, and pillars can be considered as points on the plane. The fences you make are rectangles, and you MUST make two rectangles. Please note that the rectangles you make must be parallel to the coordinate axes. 

The figures below shows 3 situations which are not qualified(Thick dots stands for pillars): 


Zhang Liang and Xiao He wanted the total area of their land in E-pang Palace to be maximum. Please bring your computer and go back to Han dynasty to help them so that you may change the history.

InputThere are no more than 15 test case. 

For each test case: 

The first line is an integer N, meaning that there are N pillars left in E-pang Palace(4 <=N <= 30). 

Then N lines follow. Each line contains two integers x and y (0 <= x,y <= 200), indicating a pillar's coordinate. No two pillars has the same coordinate. 

The input ends by N = 0.OutputFor each test case, print the maximum total area of land Zhang Liang and Xiao He could get. If it was impossible for them to build two qualified fences, print "imp".Sample Input

8
0 0
1 0
0 1
1 1
0 2
1 2
0 3
1 3
8
0 0
2 0
0 2
2 2
1 2
3 2
1 3
3 3
0

Sample Output

2
imp


题目大意：给你一些点，从这些点中选择八个点组成两个矩形，求矩形面积的最大和是多少？两个矩形不能如下图形式：

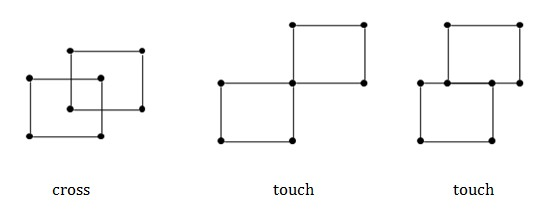
解题思路：首先使用结构体存储矩形的点，然后对于这些点有两种排序方式。方式1：对x进行由小到大的排序(既上下排序)；方式2：对y进行由小到大的排序(既左右排序)，然后对于每个找到的矩形，下一个满足条件的矩形要么在它的右边；要么在他的上边。注意：如果“回”字形的矩形我们只要求出大矩形的面积和大矩形之外的矩形的面积只和就可以了。

 

 

AC代码：

#include <iostream>
#include <bits/stdc++.h>

using namespace std;
struct node
{
    int x,y;
} a[50];
int flag[2000][2000];
int cmp2(const node &p,const node &q)
{
    if(p.x!=q.x)
        return p.x<q.x;
    else
        return p.y<q.y;
}
int cmp1(const node &p,const node &q)
{
    if(p.y!=q.y)
        return p.y<q.y;
    else
        return p.x<q.x;
}
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        if(n==0)
        break;
        memset(flag,0,sizeof(flag));
        for(int i=0; i<n; i++)
        {
            scanf("%d%d",&a[i].x,&a[i].y);
            flag[1000+a[i].x][1000+a[i].y]=1;
        }
        int maxx=0,cnt=0;
        sort(a,a+n,cmp1);
        for(int i=0; i<n; i++)
        {
            for(int j=i+1; j<n; j++)
            {
                if(a[j].x<=a[i].x||a[j].y<=a[i].y)
                    continue;
                if(flag[a[i].x+1000][a[j].y+1000]==1&&flag[a[j].x+1000][a[i].y+1000]==1)
                {
                    for(int u=i+1;u<j;u++)
                    {
                        for(int v=u+1;v<j;v++)
                        {
                            if((a[u].x>a[i].x&&a[v].x>a[u].x&&a[j].x>a[v].x)&&(a[u].y>a[i].y&&a[v].y>a[u].y&&a[j].y>a[v].y)&&(flag[a[u].x+1000][a[v].y+1000]==1&&flag[a[v].x+1000][a[u].y+1000]==1))
                            {
                               cnt=1;
                               maxx=max(maxx,(a[j].x-a[i].x)*(a[j].y-a[i].y));
                            }
                        }
                    }
                    int k;
                    for(k=0; k<n; k++)
                        if(a[k].y>a[j].y)
                            break;
                    for(int u=k; u<n; u++)
                    {
                        for(int v=u+1; v<n; v++)
                        {
                            if(a[v].x<=a[u].x||a[v].y<=a[u].y)
                                continue;
                            if(flag[a[u].x+1000][a[v].y+1000]==1&&flag[a[v].x+1000][a[u].y+1000]==1)
                            {
                                cnt=1;
                                maxx=max(maxx,(a[j].x-a[i].x)*(a[j].y-a[i].y)+(a[u].x-a[v].x)*(a[u].y-a[v].y));
                            }
                        }
                    }
                    node eps[2];
                    eps[0].x=a[i].x;
                    eps[0].y=a[i].y;
                    eps[1].x=a[j].x;
                    eps[1].y=a[j].y;
                    sort(a,a+n,cmp2);
                    for(k=0; k<n; k++)
                        if(a[k].x>eps[1].x)
                            break;
                    for(int u=k; u<n; u++)
                    {
                        for(int v=k; v<n; v++)
                        {
                            if(a[v].x<=a[u].x||a[v].y<=a[u].y)
                                continue;
                            if(flag[a[u].x+1000][a[v].y+1000]==1&&flag[a[v].x+1000][a[u].y+1000]==1)
                            {
                                cnt=1;
                                maxx=max(maxx,(eps[1].x-eps[0].x)*(eps[1].y-eps[0].y)+(a[u].x-a[v].x)*(a[u].y-a[v].y));
                            }
                        }
                    }
                }
            }
            sort(a,a+n,cmp1);
        }
        if(cnt==0)
        {
            printf("imp
");
        }
        else
        {
            printf("%d
",maxx);
        }
    }
    return 0;
}