问题简述:
Android的九宫格密码想必大家都见过了。
大于等于四个点相连便可以作为一种密码。
那么九宫格密码有多少种?
算法简述:
关键词: 组合 排列 动态规划
Android 的密码是 3 × 3 点阵中的一条路径,这条路径可以交叉,可以“走日字”,几乎是无所不能(只要不经过重复点),但却有一个例外:路径不允许跳过途中必须要经过 的点。例如, 如果从左上角的点连接到右上角的点,中间的那个点会被自动地加进路径里。但麻烦就麻烦在,这个规则本身也有一个值得注意的地方:如果中间的点是之前已经用过的,那么这个点就可以被跳过去了。
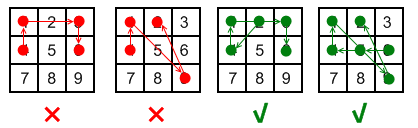
我们不妨把点阵中的九个点分别用数字 1 到 9 编号。按照上述规则,4136、4192 都是不合法的,但 24136、654192 则都是可行的。
算法思路参考:http://www.guokr.com/article/49408/
即:斜线有8条,共8对数字: 1-3前有2 1-7需有4 1-9需有5 2-8需有5
3-7需有5 3-9需有6 4-6需有5 7-9需有8 否则为失败
所以:通过动态规划遍历排列并验证(首先若i个数组合的某序列为失败,则其衍生出的后续i+1个数组合的某序列也为失败,故而不再验证,即也不会再向后动态迭代)
代码运行可知:
| 密码长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 总计 |
| 密码个数 | 9 | 56 | 320 | 1624 | 7152 | 26016 | 72912 | 140704 | 140704 | 389497 |
九宫格密码大于等于四位,故九宫格密码共有389212种,密码最好设置6位及6位以上。
代码如下:
1 package 九宫格; 2 3 public class Main{ 4 5 public static void main(String[] argv){ 6 7 // 计算组合数 8 int k[] = new int[9]; 9 int p_count[] = new int[9]; 10 int sum=0; 11 int Out_result=0; 12 13 for(int i=0; i<9;i++){ 14 15 if(i==0){ 16 k[i]=9; p_count[i]=1; 17 } 18 19 else{ 20 k[i]=k[i-1]*(9-i); 21 } 22 if(i>=3) 23 sum=sum+k[i]; 24 } 25 System.out.println(sum); 26 27 //计算排列 28 int [][] middle = new int[9][1]; 29 30 for(int i=0; i<9;i++){ 31 32 int n = k[i]; 33 int N = p_count[i]; 34 int mid_out[][] = new int[n][i+1]; 35 int pai_out[][] = new int[N][i+1]; 36 int j=0; 37 if(i==0){ 38 39 for(; j<N; j++ ) 40 pai_out[j][0]=0; 41 j=0; 42 for(; j<n; j++) 43 mid_out[j][0]=j+1; 44 j=0; 45 //更新上一次的可行序列数 46 k[i]=9; 47 } 48 else{ 49 50 // 获取排列 51 52 for(int t=0; t<k[i-1]; t++){ 53 54 int check[] =new int[10]; 55 for(int m=0; m<i;m++){ 56 57 check[middle[t][m]]=1; 58 59 } 60 for(int p=1; p<=9; p++ ){ 61 62 if(check[p]!=1){ 63 64 //排列验证成功则加入到序列中 65 if(check_Success(middle[t][i-1],p,check)){ 66 67 for(int m=0; m<i;m++){ 68 mid_out[j][m]=middle[t][m]; 69 } 70 71 mid_out[j][i]=p; 72 j++; 73 } 74 75 } 76 77 } 78 79 80 } 81 //更新上一次的可行序列数 82 k[i]=j; 83 } 84 if(i>2) 85 Out_result=Out_result+k[i]; 86 middle = new int[n][i+1]; 87 middle = mid_out; 88 for(int count_x=0; count_x<j; count_x++){ 89 System.out.print((count_x+1)+"th: "); 90 for(int count_y=0; count_y<=i;count_y++) 91 System.out.print(mid_out[count_x][count_y]+" "); 92 System.out.println(); 93 } 94 System.out.println("The"+i+"th result as..."+j); 95 96 97 } 98 99 System.out.println("The result is:"+Out_result); 100 for(int i=0; i<9; i++){ 101 102 System.out.println(k[i]); 103 } 104 } 105 106 public static boolean check_Success(int a, int b, int[] r){ 107 108 int[][] k_table = new int[10][10]; 109 // init... 110 k_table[1][3]=2; k_table[3][1]=2; 111 k_table[1][7]=4; k_table[7][1]=4; 112 k_table[1][9]=5; k_table[9][1]=5; 113 // init.... 114 k_table[2][8]=5; k_table[8][2]=5; 115 //init.... 116 k_table[3][7]=5; k_table[7][3]=5; 117 k_table[3][9]=6; k_table[9][3]=6; 118 // init.... 119 k_table[4][6]=5; k_table[6][4]=5; 120 // init.... 121 k_table[7][9]=8; k_table[9][7]=8; 122 if(k_table[a][b]>0){ 123 if(r[k_table[a][b]]==1) 124 return true; 125 else 126 return false; 127 } 128 else 129 return true; 130 131 132 } 133 }