通项、递推、递归的区别:
通项公式,是用自然数n的表达式表示数列的“通项”f(n)的公式,
递推,是由含有数列前边的若干项的表达式表示后边某一项的公式。
如果表达式中仅含数列前边的若干项(允许有常数系数),这个公式就叫递归公式。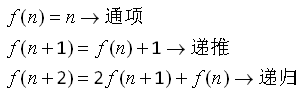
从函数方程观点看,递推,递归公式实际都是函数方程,而通项公式则是它们的解。
为了方便,把只含数列中的项(可以带有系数)的递推公式叫递归公式,一般形式: 一旦给出通项公式,数列便被唯一地确定。但递推特别是递归公式却不然,给出一个递归公式后,会有无穷多数列都满足这个递归公式,这是因为,由k阶递归公式的数列,它的前k项无法由递归公式本身确定。但给出数列的前k项的值后,递归公式就唯一地确定了数列,把数列前k项的值叫初值条件。同一个递归公式,由于初值条件不同,将得到不同的数列。
一旦给出通项公式,数列便被唯一地确定。但递推特别是递归公式却不然,给出一个递归公式后,会有无穷多数列都满足这个递归公式,这是因为,由k阶递归公式的数列,它的前k项无法由递归公式本身确定。但给出数列的前k项的值后,递归公式就唯一地确定了数列,把数列前k项的值叫初值条件。同一个递归公式,由于初值条件不同,将得到不同的数列。
这段话还是容易理解的。做一个简易例子,假如f(n+1)=2f(n),容易看出是一个等比数列,公比为2,符合这种条件的等比数列有无穷个,只有限定初项才能形成唯一一个数列。
构造首项为1,公比为q的等比数列,使它满足递归公式: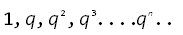 最后得到:
最后得到: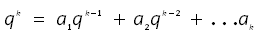 称之为递归公式的特征方程。
称之为递归公式的特征方程。
| 如果两个通项公式满足递归公式,则 1.每一项乘以一个常数仍满足 2.相乘之后,两个通项公式的各项再相加,依然符合递归公式。 |
