题目描述:
题目链接:64 Minimum Path Sum
问题是要求在一个全为正整数的 m X n 的矩阵中, 取一条从左上为起点, 走到右下为重点的路径, (前进方向只能向左或者向右),求一条所经过元素和最小的一条路径。
其实,题目已经给出了提示: , 动态规划应该是最直接的解法之一。
, 动态规划应该是最直接的解法之一。
这边我们了解到, 问题中只允许走到的每个点右移或者下移,这就意味着从起点开始, 都有两种后继路径(最后一行和最后一列除外),以此类推, 得到所有路径,然后取其中路径和虽小的值,就可以得到结果了。 但是!我们仔细想想,如果这么求解问题的话, 对于一个N X N 的矩阵, 他的可能路径条数有几条?(想想N层的二叉树的路径有几条)所以用这个思路的话, 可行, 但是不推荐,因为数据成长是O(2^N)的, 太可怕。
再想想,前面提到: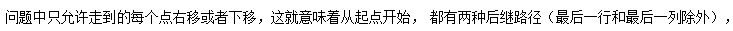
其实就是意味着: 从终点开始往前推, 都有两种前驱路径(第一行和第一列除外),最后一个点只可能从上边走下来,即为path_top或者从左边走过来path_left, 至于走哪条路, 自然是哪一条路径和小,就选择哪一条。
对于最后一个点1上边路径的最佳结果,已经从上边的红色区域中的带哦并累计到3这个点(另外需要一个路径和矩阵做记录)

对于最后一个点左边最小路径的结果,已经从左边的红色区域中得到并累积到8这个点(另外需要一个路径和矩阵做记录)
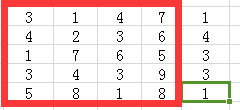
而对于以上红色区域的最后一个点, 也同样是从上层区域和左边区域已经求得的最优解来进行2选一操作, 做成最优解。
就像这样:


然后一直重复, 直到起点。
所以,对于(M,N)点处的结果, 必然是从(M-1)*N 矩阵 和 M* (N-1)矩阵中求取的,
ok, 推理到这一步, 其实问题已经解决了, 所有的问题都是从起点开始, 所有的点都是由之前点上的路径和决定的。
从最简单的情形开始:对于一个2*2的举证, [0,0] 决定了[0,1]和[1,0],

这样[1,1]的最小值肯定是从[0,1]的4 和 [1, 0]的7中比较取值, 所以最后的到在终点[1,1]的最小取值4+2 = 6;
我们定义对于走到每个点的最小路径和矩阵path_sum[m][n], 以及给出的每个点上的值矩阵matrix[m][n]
得到: path_sum[i, j] = min(path_sum[i-1][j], path_sum[i][j-1]) + matrix[m][n]
(注意, 上式中为处理边界是的情况, 只指出此递推式的核心步骤);
说的可能有点乱, 但核心思想就是尽然你每个非边界的点只能往后两条去路, 那必然非边界的每个点都肯定也只有两条来路,
最优解就是这两条来路里面2选一, done!
下面是个人的solution 代码, 仅供参考
