不等数列
【题目描述】
将1到n任意排列,然后在排列的每两个数之间根据他们的大小关系插入“>”和“<”。问在所有排列中,有多少个排列恰好有k个“<”。答案对2012取模。
【输入格式】
第一行2个整数n,k。
【输出格式】
一个整数表示答案。
【样例输入】
5 2
【样例输出】
66
【数据范围】
对于30%的数据:n <= 10
对于100%的数据:k < n <= 1000,
对于30% n<=10的数据,搜索打表,状态压缩动态规划......
对于1--n等类似的排列计数问题,以动态规划和组合数学2种大方向为基本解决方向。
组合数学在noip最难也就到杨辉三角左右,所以这题我从动态规划展开。
如果此类排列问题在脑中的模型是:“有n个格子,填入1--n”,那么相对应的DP就不得不记录哪些数填过了(从左到右填入)或者哪些格子填过了(从小到大填入)。这样一来就必须要使用状态压缩来存储这些信息,就使得复杂度变得难以接受。
而如果换个模型:“从小到大把数字插入数列”。注意是数列而不是格子,这样一来就不需要记录是哪些数字插入了(而只要记录插入到了第几个数字),同时不需要记录每个数字的具体位置,也不需要记录数字的相对位置,而只需记录相对关系的数目(对本题而言就是有几个“<”)。
因为是从小到大插入数字,所以当前插入的数字一定大于所有已经插入的。

蓝色是当前插入的数字,如果它插入到<关系的2个数字之间(或者数列最左端),就会使数列的<数量不变,>数量+1:
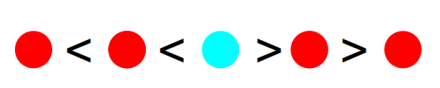
类似的,插入到>关系的2个数字之间(或者数列最右端),数列的<数量+1,>数量不变。
F[i][j]表示前i个数字构成的数列中,恰有j个‘<’号的方案数(‘>’号就有i-j-1个)。
F[i][j]=F[i-1][j-1]*(i-j)+F[i-1][j]*(j+1).
时空复杂度:O(n^2)
若打表则时间复杂度为O(1)
#include<iostream> #include<cstdio> using namespace std; int n,k,f[1010][1010]; int main(){ scanf("%d%d",&n,&k); for(int i=1;i<=n;i++)f[i][0]=1; for(int i=1;i<=n;i++) for(int j=1;j<i;j++) f[i][j]=max(f[i][j],f[i-1][j-1]*(i-j)%2012+f[i-1][j]*(j+1)%2012)%2012; cout<<f[n][k]; }