TZOJ 二分图练习

二分图主要是

1.如何建图，谁匹配谁，怎么匹配

2.判断求的是什么：最大匹配=最小点覆盖，最大独立子集=最小路径覆盖=最小边覆盖=图中顶点数-最大匹配

A.2733：棋盘游戏

描述

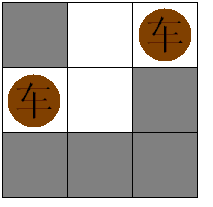
小希和Gardon在玩一个游戏：对一个N*M的棋盘，在格子里放尽量多的一些国际象棋里面的“车”，并且使得他们不能互相攻击，这当然很简单，但是Gardon限制了只有某些格子才可以放，小希还是很轻松的解决了这个问题（见下图）注意不能放车的地方不影响车的互相攻击。
所以现在Gardon想让小希来解决一个更难的问题，在保证尽量多的“车”的前提下，棋盘里有些格子是可以避开的，也就是说，不在这些格子上放车，也可以保证尽量多的“车”被放下。但是某些格子若不放子，就无法保证放尽量多的“车”，这样的格子被称做重要点。Gardon想让小希算出有多少个这样的重要点，你能解决这个问题么？

输入

输入包含多组数据，
第一行有三个数N、M、K(1<N,M<=100 1<K<=N*M)，表示了棋盘的高、宽，以及可以放“车”的格子数目。接下来的K行描述了所有格子的信息：每行两个数X和Y，表示了这个格子在棋盘中的位置。

输出

对输入的每组数据，按照如下格式输出：
Board T have C important blanks for L chessmen.

样例输入

3 3 4
1 2
1 3
2 1
2 2
3 3 4
1 2
1 3
2 1
3 2

样例输出

Board 1 have 0 important blanks for 2 chessmen.
Board 2 have 3 important blanks for 3 chessmen.

题意

给你一个n*m的棋盘，给你k个位置用于放“车”，问最多能放多少个车，然后问你放最多的“车”有几个位置是唯一的

题解

这个题一开始想到用DFS回溯去判断最多放“车”的数量，可是回溯复杂度太高了，果断不行

然后你可以发现，在X每行和Y每列只能放一个“车”，所有可以想到用二分图匹配去做

match[x]=y;给x匹配y，直接暴力跑匈牙利，求最大匹配

然后就是求“车”位置的唯一性，我们跑完匈牙利，match[x]=y;如果x有匹配则=y，否则=-1

那我们可以先把“车”放的位置去掉，G[x][match[x]]=0;再跑一遍匈牙利，若小于最大匹配，则为关键点

代码

#include<bits/stdc++.h>
using namespace std;
const int M=110;
int n,m,k,o;
int vis[M],match[M],p[M],G[M][M];
int Find(int y)//给x匹配y
{
    for(int x=1;x<=n;x++)
    {
        if(G[x][y]&&!vis[x])
        {
            vis[x]=1;
            if(match[x]==-1||Find(match[x]))
            {
                match[x]=y;
                return 1;
            }
        }
    }
    return 0;
}
int Hungary(int flag)
{
    int ans=0;
    memset(match,-1,sizeof(match));
    for(int i=1;i<=m;i++)
    {
        memset(vis,0,sizeof(vis));
        if(Find(i))ans++;
    }
    if(flag)
        for(int i=1;i<=m;i++)
            p[i]=match[i];//临时存放最大匹配
    return ans;
}
int main()
{
    while(scanf("%d%d%d",&n,&m,&k)!=EOF)
    {
        int x,y;
        memset(G,0,sizeof(G));
        for(int i=1;i<=k;i++)
        {
            scanf("%d%d",&x,&y);
            G[x][y]=1;
        }
        int maxx=Hungary(1),ip=0;
        for(int i=1;i<=n;i++)
        {
            if(p[i]==-1)continue;//x不是最大匹配点，跳过
            G[i][p[i]]=0;//删掉车点
            if(Hungary(0)<maxx)ip++;
            G[i][p[i]]=1;//还原
        }
        printf("Board %d have %d important blanks for %d chessmen.
",++o,ip,maxx);
    }
    return 0;
}

 B.2021:  Cat vs. Dog

描述

The latest reality show has hit the TV: ``Cat vs. Dog''. In this show, a bunch of cats and dogs compete for the very prestigious Best Pet Ever title. In each episode, the cats and dogs get to show themselves off, after which the viewers vote on which pets should stay and which should be forced to leave the show.

Each viewer gets to cast a vote on two things: one pet which should be kept on the show, and one pet which should be thrown out. Also, based on the universal fact that everyone is either a cat lover (i.e. a dog hater) or a dog lover (i.e. a cat hater), it has been decided that each vote must name exactly one cat and exactly one dog.

Ingenious as they are, the producers have decided to use an advancement procedure which guarantees that as many viewers as possible will continue watching the show: the pets that get to stay will be chosen so as to maximize the number of viewers who get both their opinions satisfied. Write a program to calculate this maximum number of viewers.

输入

On the first line one positive number: the number of testcases, at most 100. After that per testcase:

• One line with three integers c, d, v (1 ≤ c, d ≤ 100 and 0 ≤ v ≤ 500): the number of cats, dogs, and voters.
• v lines with two pet identifiers each. The first is the pet that this voter wants to keep, the second is the pet that this voter wants to throw out. A pet identifier starts with one of the characters `C' or `D', indicating whether the pet is a cat or dog, respectively. The remaining part of the identifier is an integer giving the number of the pet (between 1 and c for cats, and between 1 and d for dogs). So for instance, ``D42'' indicates dog number 42.

输出

Per testcase:

• One line with the maximum possible number of satisfied voters for the show.

样例输入

2
1 1 2
C1 D1
D1 C1
1 2 4
C1 D1
C1 D1
C1 D2
D2 C1

样例输出

1
3

题意

舞台上有c只猫，d只狗，台下有v个人，每个人都有喜欢的动物和讨厌的动物，如果舞台上有喜欢的并且没有讨厌的，这个人就会满足，求最大满足的人数

题解

很明显是一道二分图求最大独立集的问题，每两个人都不冲突

最大独立集=图中顶点数-最大匹配

接下来是建图的问题，首先最后要求的是所有人都不冲突，可以想到往两两冲突去建图，比如1和4冲突，那么4和1也冲突，最后人数-最大匹配/2，很幸运，这样234MS

然后有个建图的优化，把喜欢猫的放在左边，把喜欢狗的放在右边，两个集合内部没有冲突，最后人数-最大匹配，78MS

代码

#include<bits/stdc++.h>
using namespace std;
const int N=5e2+5;
int c,d,v;
int G[N][N],vis[N],match[N];
int Find(int x)//dog
{
    for(int i=0;i<v;i++)//cat
    {
        if(G[i][x]&&!vis[i])
        {
            vis[i]=1;
            if(match[i]==-1||Find(match[i]))
            {
                match[i]=x;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        char a[N][5],b[N][5];
        memset(G,0,sizeof(G));
        memset(match,-1,sizeof(match));
        scanf("%d%d%d",&c,&d,&v);
        for(int i=0;i<v;i++)
            scanf("%s%s",a[i],b[i]);
        ///G[cat][dog]
        for(int i=0;i<v;i++)
            if(a[i][0]=='C')
                for(int j=0;j<v;j++)
                    if(i!=j&&a[j][0]=='D'&&(strcmp(a[i],b[j])==0||strcmp(b[i],a[j])==0))
                        G[i][j]=1;//有冲突
        int ans=0;
        for(int i=0;i<v;i++)
        {
            memset(vis,0,sizeof(vis));
            if(Find(i))ans++;
        }
        printf("%d
",v-ans);
    }
    return 0;
}

 C.1911: A Plug for UNIX

描述

You are in charge of setting up the press room for the inaugural meeting of the United Nations Internet eXecutive (UNIX), which has an international mandate to make the free flow of information and ideas on the Internet as cumbersome and bureaucratic as possible.
Since the room was designed to accommodate reporters and journalists from around the world, it is equipped with electrical receptacles to suit the different shapes of plugs and voltages used by appliances in all of the countries that existed when the room was built. Unfortunately, the room was built many years ago when reporters used very few electric and electronic devices and is equipped with only one receptacle of each type. These days, like everyone else, reporters require many such devices to do their jobs: laptops, cell phones, tape recorders, pagers, coffee pots, microwave ovens, blow dryers, curling
irons, tooth brushes, etc. Naturally, many of these devices can operate on batteries, but since the meeting is likely to be long and tedious, you want to be able to plug in as many as you can.
Before the meeting begins, you gather up all the devices that the reporters would like to use, and attempt to set them up. You notice that some of the devices use plugs for which there is no receptacle. You wonder if these devices are from countries that didn't exist when the room was built. For some receptacles, there are several devices that use the corresponding plug. For other receptacles, there are no devices that use the corresponding plug.
In order to try to solve the problem you visit a nearby parts supply store. The store sells adapters that allow one type of plug to be used in a different type of outlet. Moreover, adapters are allowed to be plugged into other adapters. The store does not have adapters for all possible combinations of plugs and receptacles, but there is essentially an unlimited supply of the ones they do have.

输入

The input will consist of one case. The first line contains a single positive integer n (1 <= n <= 100) indicating the number of receptacles in the room. The next n lines list the receptacle types found in the room. Each receptacle type consists of a string of at most 24 alphanumeric characters. The next line contains a single positive integer m (1 <= m <= 100) indicating the number of devices you would like to plug in. Each of the next m lines lists the name of a device followed by the type of plug it uses (which is identical to the type of receptacle it requires). A device name is a string of at most 24 alphanumeric
characters. No two devices will have exactly the same name. The plug type is separated from the device name by a space. The next line contains a single positive integer k (1 <= k <= 100) indicating the number of different varieties of adapters that are available. Each of the next k lines describes a variety of adapter, giving the type of receptacle provided by the adapter, followed by a space, followed by the type of plug.

输出

A line containing a single non-negative integer indicating the smallest number of devices that cannot be plugged in.

样例输入

4
A
B
C
D
5
laptop B
phone C
pager B
clock B
comb X
3
B X
X A
X D

样例输出

1

题解

据说是用网络流写的二分图匹配，我太菜了没写出

 D.2380: Gopher II

描述

The gopher family, having averted the canine threat, must face a new predator.

The are n gophers and m gopher holes, each at distinct (x, y) coordinates. A hawk arrives and if a gopher does not reach a hole in s seconds it is vulnerable to being eaten. A hole can save at most one gopher. All the gophers run at the same velocity v. The gopher family needs an escape strategy that minimizes the number of vulnerable gophers.

输入

The input contains several cases. The first line of each case contains four positive integers less than 100: n, m, s, and v. The next n lines give the coordinates of the gophers; the following m lines give the coordinates of the gopher holes. All distances are in metres; all times are in seconds; all velocities are in metres per second.

输出

Output consists of a single line for each case, giving the number of vulnerable gophers.

样例输入

2 2 5 10
1.0 1.0
2.0 2.0
100.0 100.0
20.0 20.0

样例输出

1

题意

有n个地鼠，m个洞，老鹰s秒后会吃掉所有不在洞里的地鼠，地鼠以v的速度跑到洞里就可以避免被吃掉，求最后被吃了几个

题解

一开始vulnerable gophers以为是幸存的数量，wa？？？后来发现是vulnerable gophers脆弱的地鼠数量，英语太渣了

一道模板二分最大匹配，由于最大匹配是可以到洞里，所以最后地鼠总数-最大匹配

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e2+5;
int m,n;
int G[N][N],vis[N],match[N];
struct p{double x,y;}d[N];
int Find(int x)//地鼠
{
    for(int i=0;i<m;i++)//洞
    {
        if(G[x][i]&&!vis[i])
        {
            vis[i]=1;
            if(match[i]==-1||Find(match[i]))
            {
                match[i]=x;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    int s,v;
    while(scanf("%d%d%d%d",&n,&m,&s,&v)!=EOF)
    {
        memset(G,0,sizeof(G));
        memset(match,-1,sizeof(match));
        double dis=s*1.0*v;
        for(int i=0;i<n;i++)//地鼠位置
            scanf("%lf%lf",&d[i].x,&d[i].y);
        for(int i=0;i<m;i++)//洞的位置
        {
            double x,y;
            scanf("%lf%lf",&x,&y);
            for(int j=0;j<n;j++)
            {
                if(sqrt( (d[j].x-x)*(d[j].x-x)+(d[j].y-y)*(d[j].y-y) )<=dis)
                    G[j][i]=1;
            }
        }
        int ans=0;
        for(int i=0;i<n;i++)
        {
            memset(vis,0,sizeof(vis));
            if(Find(i))ans++;
        }
        printf("%d
",n-ans);
    }
    return 0;
}

 E.1023: Taxi Cab Scheme

描述

Running a taxi station is not all that simple. Apart from the obvious demand for a centralised coordination of the cabs in order to pick up the customers calling to get a cab as soon as possible,there is also a need to schedule all the taxi rides which have been booked in advance.Given a list of all booked taxi rides for the next day, you want to minimise the number of cabs needed to carry out all of the rides.
For the sake of simplicity, we model a city as a rectangular grid. An address in the city is denoted by two integers: the street and avenue number. The time needed to get from the address a, b to c, d by taxi is |a - c| + |b - d| minutes. A cab may carry out a booked ride if it is its first ride of the day, or if it can get to the source address of the new ride from its latest,at least one minute before the new ride's scheduled departure. Note that some rides may end after midnight.

输入

On the first line of the input is a single positive integer N, telling the number of test scenarios to follow. Each scenario begins with a line containing an integer M, 0 < M < 500, being the number of booked taxi rides. The following M lines contain the rides. Each ride is described by a departure time on the format hh:mm (ranging from 00:00 to 23:59), two integers a b that are the coordinates of the source address and two integers c d that are the coordinates of the destination address. All coordinates are at least 0 and strictly smaller than 200. The booked rides in each scenario are sorted in order of increasing departure time.

输出

For each scenario, output one line containing the minimum number of cabs required to carry out all the booked taxi rides.

样例输入

2
2
08:00 10 11 9 16
08:07 9 16 10 11
2
08:00 10 11 9 16
08:06 9 16 10 11

样例输出

1
2

题意

t组数据，每组数据给你n个乘客，然后n行为乘客上车的时间，乘客的初始位置，乘客要到的位置，已知出租车从（a，b）->（c，d）需要花费分钟，出租车需要提前至少1分钟到达乘客的初始位置才能接到，求最少需要准备多少车

题解

一道求二分图最小路径覆盖==最大匹配

直接按出两个乘客间出租车能否都到建图，求最大匹配即可

代码

尝试下函数大法，这个好理解？？？（我的错觉）

#include<bits/stdc++.h>
using namespace std;
const int N=5e2+5;
struct p
{
    int st,a,b,c,d,et;
}d[N];
int n;
inline int Dis(int a,int b,int c,int d)
{
    return fabs(a-c)+fabs(b-d);
}
void Read()
{
    int h,m;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d:%d%d%d%d%d",&h,&m,&d[i].a,&d[i].b,&d[i].c,&d[i].d);
        d[i].st=h*60+m;
        d[i].et=d[i].st+Dis(d[i].a,d[i].b,d[i].c,d[i].d);
    }
}
int G[N][N];//i->j ok
void Build_Map()
{
    memset(G,0,sizeof G);
    for(int i=0;i<n;i++)
        for(int j=i+1;j<n;j++)
            G[i][j]=d[i].et+Dis(d[i].c,d[i].d,d[j].a,d[j].b)+1<=d[j].st;
}
int match[N],vis[N];//j---i
int Find(int i)//i
{
    for(int j=i+1;j<n;j++)//j
    {
        if(G[i][j]&&!vis[j])
        {
            vis[j]=1;
            if(match[j]==-1||Find(match[j]))
            {
                match[j]=i;
                return 1;
            }
        }
    }
    return 0;
}
void Work()
{
    memset(match,-1,sizeof match);
    int ans=0;
    for(int i=0;i<n;i++)
    {
        memset(vis,0,sizeof vis);
        if(Find(i))ans++;
    }
    //printf("ans==%d
",ans);
    printf("%d
",n-ans);
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        Read();
        Build_Map();
        Work();
    }
    return 0;
}

 F.1037: Guardian of Decency

描述

Frank N. Stein is a very conservative high-school teacher. He wants to take some of his students on an excursion, but he is afraid that some of them might become couples. While you can never exclude this possibility, he has made some rules that he thinks indicates a low probability two persons will become a couple:

• Their height differs by more than 40 cm.
• They are of the same sex.
• Their preferred music style is different.
• Their favourite sport is the same (they are likely to be fans of different teams and that would result in fighting).

So, for any two persons that he brings on the excursion, they must satisfy at least one of the requirements above. Help him find the maximum number of persons he can take, given their vital information

输入

The first line of the input consists of an integer T ≤ 100 giving the number of test cases. The first line of each test case consists of an integer N ≤ 500 giving the number of pupils. Next there will be one line for each pupil consisting of four space-separated data items:

• an integer h giving the height in cm;
• a character 'F' for female or 'M' for male;
• a string describing the preferred music style;
• a string with the name of the favourite sport.

No string in the input will contain more than 100 characters, nor will any string contain any whitespace.

输出

For each test case in the input there should be one line with an integer giving the maximum number of eligible pupils.

样例输入

2
4
35 M classicism programming
0 M baroque skiing
43 M baroque chess
30 F baroque soccer
8
27 M romance programming
194 F baroque programming
67 M baroque ping-pong
51 M classicism programming
80 M classicism Paintball
35 M baroque ping-pong
39 F romance ping-pong
110 M romance Paintball

样例输出

3
7

题意

t组数据，每组1个n行，身高，性别，偏好的音乐风格，喜欢的球队

为了尽量避免两人成为情侣，Frank N. Stein制定了一些规则防止两人成为情侣

1.身高差距>40cm

2.同性

3.偏好的音乐风格不同

4.喜欢的球队相同

题解

一道求二分图最大独立集=总人数-最大匹配

还是建图问题

如果按i和j能组成情侣连建图G[i][j]=1，最后总人数-最大匹配/2

如果按男女建图，最后总人数-最大匹配

代码

#include<bits/stdc++.h>
using namespace std;
const int N=5e2+5;
struct p
{
    int h;
    string sex,mus,spo;
}d[N];
int n;
void Read()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>d[i].h>>d[i].sex>>d[i].mus>>d[i].spo;
}
int G[N][N];
void Build_Map()
{
    //G[][]boy,girl,无向图
    memset(G,0,sizeof G);
    for(int i=0;i<n;i++)
        if(d[i].sex=="M")
            for(int j=0;j<n;j++)
                if(d[j].sex=="F"&&fabs(d[i].h-d[j].h)<=40&&d[i].mus==d[j].mus&&d[i].spo!=d[j].spo)
                    G[i][j]=1;
}
int match[N],vis[N];//girl--boy
int Find(int boy)
{
    for(int girl=0;girl<n;girl++)
    {
        if(G[boy][girl]&&!vis[girl])
        {
            vis[girl]=1;
            if(match[girl]==-1||Find(match[girl]))
            {
                match[girl]=boy;
                return 1;
            }
        }
    }
    return 0;
}
void Slove()
{
    memset(match,-1,sizeof match);
    int ans=0;
    for(int i=0;i<n;i++)
    {
        memset(vis,0,sizeof vis);
        if(Find(i))ans++;
    }
    cout<<n-ans<<endl;
}
int main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int t;
    cin>>t;
    while(t--)
    {
        Read();
        Build_Map();
        Slove();
    }
    return 0;
}

 F.3127: National Treasures

描述

The great hall of the national museum has been robbed few times recently. Everyone is now worried about the security of the treasures on display. To help secure the hall, the museum contracted with a private security company to provide additional guards to stay in the great hall and keep an eye on the ancient artifacts. The museum would like to hire the minimum number of additional guards so that the great hall is secured.
The great hall is represented as a two dimensional grid of R × C cells. Some cells are already occupied with the museum’s guards. All remaining cells are occupied by artifacts of different types (statues, sculptures, . . . etc.) which can be replaced by new hired guards. For each artifact, few other cells in the hall are identified as critical points of the artifact depending on the artifact value, type of vault it is kept inside, and few other factors. In other words, if this artifact is going to stay in the hall then all of its critical points must have guards standing on them. A guard standing in a critical position of multiple artifacts can keep an eye on them all. A guard, however,
can not stand in a cell which contains an artifact (instead, you may remove the artifact to allow the guard to stay there). Also you can not remove an artifact and leave the space free (you can only replace an artifact with a new hired guard).
Surveying all the artifacts in the great hall you figured out that the critical points of any artifact (marked by a ) are always a subset of the 12 neighboring cells as shown in the grid below.



Accordingly, the type of an artifact can be specified as a non-negative integer where the i-th bit is 1 only if critical point number i from the picture above is a critical point of that artifact. For example an artifact of type 595 (in binary 1001010011) can be pictured as shown in the figure below. Note that bits are numbered from right to left (the right-most bit is bit number 1.) If a critical point of an artifact lies outside the hall grid then it is considered secure.



You are given the layout of the great hall and are asked to find the minimum number of additional guards to hire such that all remaining artifacts are secured.

输入

Your program will be tested on one or more test cases. Each test case is specified using R+1 lines.
The first line specifies two integers (1<= R,C <= 50) which are the dimensions of the museum hall. The next R lines contain C integers separated by one or more spaces. The j-th integer of the i-th row is -1 if cell (i, j) already contains one of the museum’s guards, otherwise it contains an integer (0 <= T <= 2¹²) representing the type of the artifact in that cell.
The last line of the input file has two zeros.

输出

For each test case, print the following line:
k. G
Where k is the test case number (starting at one,) and G is the minimum number of additional guards to hire such that all remaining artifacts are secured.

样例输入

1 3
512 -1 2048
2 3
512 2560 2048
512 2560 2048
0 0

样例输出

1. 0
2. 2

 

提示

The picture below shows the solution of the second test case where the two artifacts in the middle are replaced by guards. 

题解

暂时不会写，太菜了

 F.3635: 过山车

描述

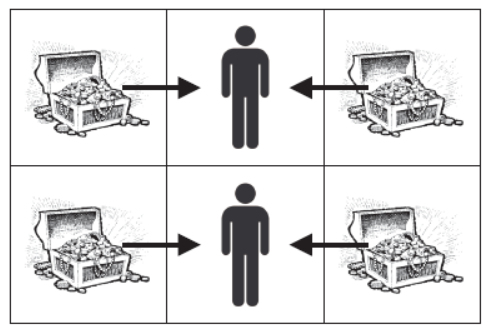
RPG girls今天和大家一起去游乐场玩，终于可以坐上梦寐以求的过山车了。可是，过山车的每一排只有两个座位，而且还有条不成文的规矩，就是每个女生必须找个个男生做partner和她同坐。但是，每个女孩都有各自的想法，举个例子把，Rabbit只愿意和XHD或PQK做partner，Grass只愿意和linle或LL做partner，PrincessSnow愿意和水域浪子或伪酷儿做partner。考虑到经费问题，boss刘决定只让找到partner的人去坐过山车，其他的人，嘿嘿，就站在下面看着吧。聪明的Acmer，你可以帮忙算算最多有多少对组合可以坐上过山车吗？

输入

输入数据的第一行是三个整数K , M , N，分别表示可能的组合数目，女生的人数，男生的人数。0<K<=1000
1<=N 和M<=500.接下来的K行，每行有两个数，分别表示女生Ai愿意和男生Bj做partner。最后一个0结束输入。

输出

对于每组数据，输出一个整数，表示可以坐上过山车的最多组合数。

样例输入

6 3 3
1 1
1 2
1 3
2 1
2 3
3 1
0

样例输出

3

题意

如上

题解

求二分图最大匹配，图都给你建好了，很esay

代码

#include<bits/stdc++.h>
using namespace std;
const int N=5e2+5;
int k,m,n;
int G[N][N],vis[N],match[N];//给男生匹配女生
int Find(int x)
{
    for(int i=1;i<=n;i++)//男生
    {
        if(G[x][i]&&!vis[i])
        {
            vis[i]=1;
            if(match[i]==-1||Find(match[i]))
            {
                match[i]=x;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    while(scanf("%d",&k)!=EOF,k)
    {
        memset(G,0,sizeof(G));
        scanf("%d%d",&m,&n);
        for(int i=0;i<k;i++)
        {
            int boy,girl;
            scanf("%d%d",&girl,&boy);
            G[girl][boy]=1;
        }
        memset(match,-1,sizeof(match));
        int ans=0;
        for(int i=1;i<=m;i++)//女生
        {
            memset(vis,0,sizeof(vis));
            if(Find(i))ans++;
        }
        printf("%d
",ans);
    }
    return 0;
}