python: 深度学习-梯度

梯度的实现：

import numpy as np

def numerical_gradient(f,x):     
    #数值微分求梯度,f为函数，x为NumPy数组，该函数对数组x的各个元素求数值微分
    
    h=1e-4#0.0001
    grad=np.zeros_like(x)#生成和x形状相同的数组
    
    for idx in range(x.size):
        tmp_val=x[idx]
        #f(x+h)的计算
        x[idx]=tmp_val+h
        fxh1=f(x)
        
        #f(x-h)的计算
        x[idx]=tmp_val-h
        fxh2=f(x)
        
        grad[idx]=(fxh1-fxh2)/(2*h)
        x[idx]=tmp_val #还原值
        
    return grad
    
def function_2(x):
    return x[0]**2+x[1]**2
    
print(numerical_gradient(function_2,np.array([3.0,4.0])))

梯度下降法的实现：

def gradient_descent(f,init_x,lr=0.01,step_num=100):  #f是函数
    x=init_x  #init_x是初始值
    
    for i in range(step_num):
        grad=numerical_gradient(f,x)
        x-=lr*grad
        
    return x

神经网络的梯度

　　　　

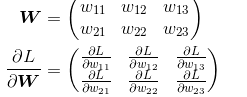
下面，我们以一个简单的神经网络为例，来实现求梯度的代码：

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 为了导入父目录中的文件而进行的设定
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient


class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2,3)

    def predict(self, x):
        return np.dot(x, self.W)

    def loss(self, x, t):
        z = self.predict(x)     #z=xW
        y = softmax(z)
        loss = cross_entropy_error(y, t)    #交叉熵误差

        return loss

x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])

net = simpleNet()

f = lambda w: net.loss(x, t)   #f是损失函数
dW = numerical_gradient(f, net.W)       

print(dW)

学习算法的实现：

前提

神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的过程称为“学习”。神经网络的学习分成下面 4 个步骤。

步骤 1（mini-batch）

从训练数据中随机选出一部分数据，这部分数据称为 mini-batch。我们的目标是减小 mini-batch 的损失函数的值。

步骤 2（计算梯度）

为了减小 mini-batch 的损失函数的值，需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。

步骤 3（更新参数）

将权重参数沿梯度方向进行微小更新。

步骤 4（重复）

重复步骤 1、步骤 2、步骤 3。

2层神经网络的类：

import sys,os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient

class TwoLayerNet:
    def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
        #初始化权重
        self.params={}
        self.params['W1']=weight_init_std*np.random.randn(input_size,hidden_size)
        self.params['b1']=np.zeros(hidden_size)
        self.params['W2']=weight_init_std*np.random.randn(hidden_size,output_size)
        self.params['b2']=np.zeros(output_size)
        
    def predict(self,x):
        W1,W2=self.params['W1'],self.params['W2']
        b1,b2=self.params['b1'],self.params['b2']
        
        a1=np.dot(x,W1)+b1
        z1=sigmoid(a1)
        a2=np.dot(z1,W2)+b2
        y=softmax(a2)
        
        return y
        
    def loss(self,x,t):
        y=self.predict(x)
        
        return cross_entropy_error(y,t)
        
    def accuracy(self,x,t):
        y=self.predict(x)
        y=np.argmax(y,axis=1)
        t=np.argmax(t,axis=1)
        
        accuracy=np.sum(y==t)/float(x.shape[0])
        return accuracy
        
    def numerical_gradient(self,x,t):
        loss_W=lambda W: self.loss(x,t)
        
        grads={}
        grads['W1']=numerical_gradient(loss_W,self.params['W1'])
        grads['b1']=numerical_gradient(loss_W,self.params['b1'])
        grads['W2']=numerical_gradient(loss_W,self.params['W2'])
        grads['b2']=numerical_gradient(loss_W,self.params['b2'])
        
        return grads

 mini-batch的实现：

import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

(x_train, t_train), (x_test, t_test) =  load_mnist(normalize=True, one_hot_
label = True)

train_loss_list = []

# 超参数
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

for i in range(iters_num):
    # 获取mini-batch
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    # 计算梯度
    grad = network.numerical_gradient(x_batch, t_batch)
    # grad = network.gradient(x_batch, t_batch) # 高速版!

    # 更新参数
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    # 记录学习过程
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)