1. 导读
本节内容介绍普通RNN的弊端,从而引入各种变体RNN,主要讲述GRU与LSTM的工作原理。
事先声明,本人采用ng在课堂上所使用的符号系统,与某些学术文献上的命名有所不同,不过核心思想都是相同的。
2. 普通RNN的弊端
- 在NLP中,句子内部以及句子之间可能存在很长的依赖关系(long-term dependecies),最前边的单词对句子后面的单词产生影响。但是普通RNN不擅长捕获这种长期依赖关系。因为RNN相当于很深的权重共享的神经网络,因此在反向传播的过程中存在很严重的梯度消失现象,损失函数得到的输出误差很难影响到前面层的计算。
- 对于深度神经网络,不光存在梯度消失,也存在梯度爆炸的现象,以至于网络参数崩溃(当参数梯度指数级增长时,你会看到很多参数值为NaN,这意味着网络发生了数值溢出)。普通RNN也是如此,但是相比于梯度消失,梯度爆炸比较容易解决,可以采用梯度修剪(gradient clipping)的处理方法。
梯度修剪,指当梯度向量大于某个阈值时,re-scale梯度向量,保证它不会数值爆炸。
3. GRU
3.1 简化GRU(便于理解)
与普通RNN相比,GRU添加了门控单元,改变了RNN的隐藏层,使得其能更好捕获长距离依赖关系,并且有效解决了梯度消失问题。下面对GRU进行详细的介绍:
- 在GRU中,人们引入了新的概念,memory cell,用符号(c)来表示,其提供了记忆能力。比如在英文句子中,网络能够记住前文的主语是单数还是复数,因此当网络看到之后的动词,仍然可以联想到前文的主语 。
- 在GRU中,(t)时刻有(c^{<t>}=a^{<t>}),(a^{<t>})是t时刻的激活值。尽管这两个值相同,我们仍然用两个不同的符号来表示,因为其分别是记忆细胞的值与输出的激活值,在LSTM中二者并不相同。 在每个时间戳,我们将用一个候选值( ilde{c}^{<t>})重写记忆细胞,每一时刻都对其进行更新。
- 在每个时间戳(t)中,需要用上一时刻的记忆细胞(c^{<t-1>}),以及当前时刻的候选值( ilde{c}^{<t>}),来更新当前时刻的记忆细胞(c^{<t>})。
- GRU最重要的思想是让我们拥有了一个叫做(gamma_u)(下标(u)代表更新门 )的门,该值位于0到1之间,该门用来决定,在每个时刻该如何更新记忆细胞的值。
以下是简化GRU的计算公式:
[ ilde{c}^{<t>}=tanh(W_c[c^{<t-1>},x^{<t>}]+b_c)
]
[gamma_u = sigma (W_u[c^{<t-1>},x^{<t>}]+b_u)
]
[c^{<t>}=gamma_u * ilde{c}^{<t>} + (1-gamma_u) * c^{<t-1>}
]
[a^{<t>} = c^{<t>}
]
GRU实现细节:
- (c^{<t>})、( ilde{c}^{<t>})、(gamma_u)是具有相同维度的向量,因此在更新(c^{<t>})时,(gamma_u * ilde{c}^{<t>})中的(*)代表向量间的点乘操作。
3.2 Full GRU (完整版本)
通过上文的介绍,相信你已经对GRU有了简单的理解,出于入门的考虑,上述GRU并不完整,这里将介绍其余下的部分。
以下是完整GRU的计算公式:
[ ilde{c}^{<t>}=tanh(W_c[gamma_r * c^{<t-1>},x^{<t>}]+b_c)
]
[gamma_u = sigma (W_u[c^{<t-1>},x^{<t>}]+b_u)
]
[gamma_r = sigma (W_r[c^{<t-1>},x^{<t>}]+b_r)
]
[c^{<t>}=gamma_u * ilde{c}^{<t>} + (1-gamma_u) * c^{<t-1>}
]
[a^{<t>} = c^{<t>}
]
这里引入了另一个门(gamma_r)——the relevance gate。
ng在课上讲,可以认为r代表相关性,(gamma_r)门告诉你计算出的( ilde{c}^{<t>})与(c^{<t-1>})有多大的相关性。
我对GRU中“门”这一概念的理解如下:
- 无论是(gamma_u),还是(gamma_r),其本质都是一个线性函数通过激活函数(sigmoid)得到的激活值,而该线性函数是以(x^{<t>}),(c^{<t-1>})作为输入。
- 也就是说,每个门的向量值是由(x^{<t>}),(c^{<t-1>})这两个值以及线性函数的权重、偏置计算得到的。
- 反向传播通过梯度下降改变线性函数的参数来改变门的向量值。
4. LSTM
LSTM存在很多变体,这里介绍经典LSTM。
4.1 经典LSTM
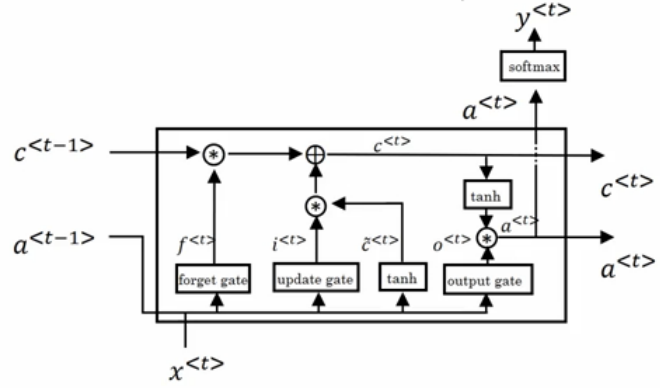
LSTM的计算公式如下所示((a^{<t>})指时刻t的隐状态):
[ ilde{c}^{<t>}=tanh(W_c[a^{<t-1>},x^{<t>}]+b_c)
]
[gamma_u = sigma (W_u[a^{<t-1>},x^{<t>}]+b_u)
]
[gamma_f = sigma (W_f[a^{<t-1>},x^{<t>}]+b_f)
]
[gamma_o = sigma (W_o[a^{<t-1>},x^{<t>}]+b_o)
]
[c^{<t>}=gamma_u * ilde{c}^{<t>} + gamma_f * c^{<t-1>}
]
[a^{<t>} = gamma_o * tanh(c^{<t>})
]
LSTM与GRU的区别:
- LSTM中有三个门,分别是更新门(gamma_u),遗忘门(gamma_f),输出门(gamma_o)。
- LSTM中使用遗忘门(gamm_f),来代替GRU中的系数((1-gamma_u)),这样是的模型更加完备,但是也引入更多的学习参数。
- LSTM的三个门,实际上是线性函数的激活值(sigmoid),而线性函数的输入是(a^{t-1}),(x^{<t>})。
有些论文提到了peephole connection这一概念,其目的是为了LSTM在计算门值的时候能够获得上一时刻(c^{<t-1>})的信息,即将线性函数的输入扩增为(a^{t-1}),(x^{<t>}),(c^{<t-1>})。
(c^{<t-1>})与(gamma_u)、(gamma_f)、(gamma_o)是维度相同的向量。(c^{<t-1>})的每个维度,与三个门的每个维度一一对应,(c^{<t-1>})中每个维度的数值只会影响到三个门中对应维度的数值。