向量
接口与实现
ADT接口
数据结构 = 基于某种特定语言,实现ADT的一整套算法
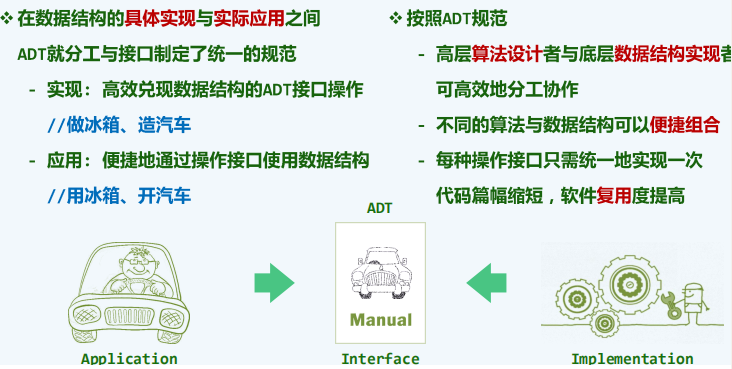
作为一种抽象数据类型,向量对象支持以下接口:

操作实例

模板类
*
* 向量模板
*0009 typedef int Rank; //秩
* 0010 #define DEFAULT_CAPACITY 3 //默认的初始容量(实际应用中可设置为更大)
* 0011
* 0012 template <typename T> class Vector { //向量模板类
* 0013 protected:
* 0014 Rank _size; int _capacity; T* _elem; //规模、容量、数据区
* 0015 void copyFrom ( T const* A, Rank lo, Rank hi ); //复制数组区间A[lo, hi)
* 0016 void expand(); //空间不足时扩容
* 0017 void shrink(); //装填因子过小时压缩
* 0018 bool bubble ( Rank lo, Rank hi ); //扫描交换
* 0019 void bubbleSort ( Rank lo, Rank hi ); //起泡排序算法
* 0020 Rank max ( Rank lo, Rank hi ); //选取最大元素
* 0021 void selectionSort ( Rank lo, Rank hi ); //选择排序算法
* 0022 void merge ( Rank lo, Rank mi, Rank hi ); //归并算法
* 0023 void mergeSort ( Rank lo, Rank hi ); //归并排序算法
* 0024 void heapSort ( Rank lo, Rank hi ); //堆排序(稍后结合完全堆讲解)
* 0025 Rank partition ( Rank lo, Rank hi ); //轴点构造算法
* 0026 void quickSort ( Rank lo, Rank hi ); //快速排序算法
* 0027 void shellSort ( Rank lo, Rank hi ); //希尔排序算法
* 0028 public:
* 0029 // 构造函数
* 0030 Vector ( int c = DEFAULT_CAPACITY, int s = 0, T v = 0 ) //容量为c、规模为s、所有元素初始为v
* 0031 { _elem = new T[_capacity = c]; for ( _size = 0; _size < s; _elem[_size++] = v ); } //s<=c
* 0032 Vector ( T const* A, Rank n ) { copyFrom ( A, 0, n ); } //数组整体复制
* 0033 Vector ( T const* A, Rank lo, Rank hi ) { copyFrom ( A, lo, hi ); } //区间
* 0034 Vector ( Vector<T> const& V ) { copyFrom ( V._elem, 0, V._size ); } //向量整体复制
* 0035 Vector ( Vector<T> const& V, Rank lo, Rank hi ) { copyFrom ( V._elem, lo, hi ); } //区间
* 0036 // 析构函数
* 0037 ~Vector() { delete [] _elem; } //释放内部空间
* 0038 // 只读访问接口
* 0039 Rank size() const { return _size; } //规模
* 0040 bool empty() const { return !_size; } //判空
* 0041 Rank find ( T const& e ) const { return find ( e, 0, _size ); } //无序向量整体查找
* 0042 Rank find ( T const& e, Rank lo, Rank hi ) const; //无序向量区间查找
* 0043 Rank search ( T const& e ) const //有序向量整体查找
* 0044 { return ( 0 >= _size ) ? -1 : search ( e, 0, _size ); }
* 0045 Rank search ( T const& e, Rank lo, Rank hi ) const; //有序向量区间查找
* 0046 // 可写访问接口
* 0047 T& operator[] ( Rank r ); //重载下标操作符,可以类似于数组形式引用各元素
* 0048 const T& operator[] ( Rank r ) const; //仅限于做右值的重载版本
* 0049 Vector<T> & operator= ( Vector<T> const& ); //重载赋值操作符,以便直接克隆向量
* 0050 T remove ( Rank r ); //删除秩为r的元素
* 0051 int remove ( Rank lo, Rank hi ); //删除秩在区间[lo, hi)之内的元素
* 0052 Rank insert ( Rank r, T const& e ); //插入元素
* 0053 Rank insert ( T const& e ) { return insert ( _size, e ); } //默认作为末元素插入
* 0054 void sort ( Rank lo, Rank hi ); //对[lo, hi)排序
* 0055 void sort() { sort ( 0, _size ); } //整体排序
* 0056 void unsort ( Rank lo, Rank hi ); //对[lo, hi)置乱
* 0057 void unsort() { unsort ( 0, _size ); } //整体置乱
* 0058 int deduplicate(); //无序去重
* 0059 int uniquify(); //有序去重
* 0060 // 遍历
* 0061 void traverse ( void (* ) ( T& ) ); //遍历(使用函数指针,只读或局部性修改)
* 0062 template <typename VST> void traverse ( VST& ); //遍历(使用函数对象,可全局性修改)
* 0063 }; //Vector
*
*
构造方法
public void copyFrom(Collection<T> A, int lo, int hi){//泛型:https://www.cnblogs.com/coprince/p/8603492.html
T[] _elem = new T[2 * (hi - lo)];//分配空间
int _size = 0;
while(lo < hi){
_elem[_size++] = A[lo++];
}
}
*
* public Vector(Collection<? extends E> c) {
* //将集合Collection转化为Object数组elementData。如果c为空,那么就会报空指针异常
* elementData = c.toArray();
* elementCount = elementData.length;
* //将c中的元素拷贝到elementData中
* if (elementData.getClass() != Object[].class)
* elementData = Arrays.copyOf(elementData, elementCount, Object[].class);
* }

扩充与缩减
对于静态空间,在添加元素时会出现上溢和下溢,因此需要对空间进行动态管理

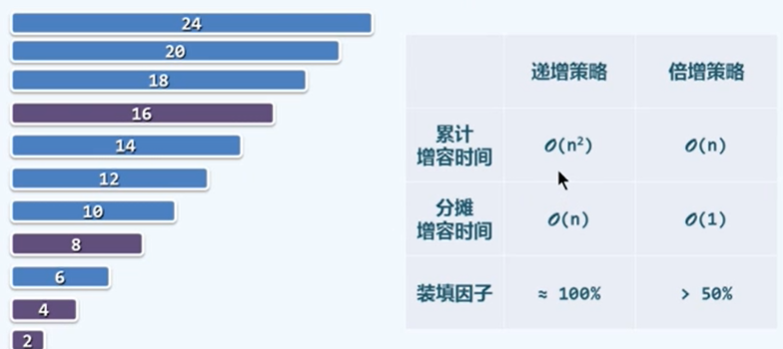
扩容
容量递增的策略:每次增加为原来的两倍(只是表示意思,下面代码并没有全写上,可能是错的)

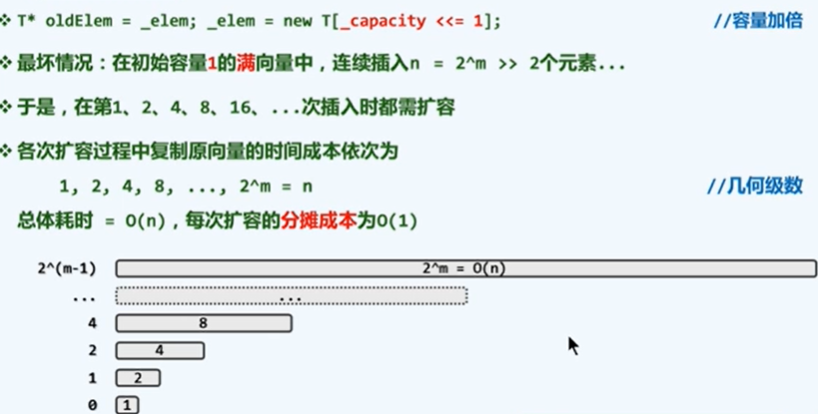
//二倍增容
public void expand(int _size,int _capacity,int DEFAULT_CAPACITY,Collection<T> oldElem){
if (_size < _capacity){
return;
}
_capacity = Math.max(_capacity,DEFAULT_CAPACITY);
T[] _elem = new T[_capacity <<= 1];
for (int i = 0; i < _size;i++){
_elem[i] = oldElem[i];
}
}
/**vertor源码上的
* 增加此向量的容量(如有必要),以确保其至少能够保存最小容量参数指定的组件数。
* 如果当前数组的容量小于minCapacity,那么就增加容量,增加数组长度
* 新数组的长度等于原数组的长度加上增量capacityIncrement。
* 如果增加capacityIncrement小于等于0,那么就自动扩增为原来二倍。
* 如果扩增为原来的二倍还是比minCapacity小,那么就将minCapacity作为Object数组的长度。
*/
public synchronized void ensureCapacity(int minCapacity) {
if (minCapacity > 0) {
modCount++;
ensureCapacityHelper(minCapacity);
}
}
private void ensureCapacityHelper(int minCapacity) {
//minCapacity为实际向量中的元素需要的容量,如果minCapacity大于当前数组长度,那么就进行扩容
if (minCapacity - elementData.length > 0)
grow(minCapacity);
}
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
private void grow(int minCapacity) {
//oldCapacity旧容量是Object数组的长度
int oldCapacity = elementData.length;
//如果增量capacityIncrement大于0,那么新容量为旧容量加上增量,否则为旧容量的2倍
int newCapacity = oldCapacity + ((capacityIncrement > 0) ?
capacityIncrement : oldCapacity);
//如果新容量小于实际需要的容量,就将实际需要的容量赋值给新容量
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
//新容量比数组的最大容量还大,就进行扩容为最大容量
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
//原先的数据域中逐一取出各项转移到新的数据域中
elementData = Arrays.copyOf(elementData, newCapacity);
}
private static int hugeCapacity(int minCapacity) {
//如果实际需要的容量小于0就抛出异常
if (minCapacity < 0)
throw new OutOfMemoryError();
//实际容量如果比最大容量还大,那么实际容量为Integer.MAX_VALUE,否则为Integer.MAX_VALUE - 8
return (minCapacity > MAX_ARRAY_SIZE) ?
Integer.MAX_VALUE :
MAX_ARRAY_SIZE;
}
缩容

@Test
public void shrink(int _size,int _capacity,int DEFAULT_CAPACITY,Collection<T> oldElem){
if (_capacity < DEFAULT_CAPACITY << 1){//不致收缩到DEFAULT_CAPACITY以下
return;
}
if (_capacity < _size << 2){//以25%为界
return;
}
T[] _elem = new T[_capacity <<= 1];
for (int i = 0; i < _size;i++){
_elem[i] = oldElem[i];
}
}
致乱算法

@Test
public void permute(Collection<T> A){
for (int i = A.size();i > 0;i--){
int math = (int)(Math.random()*A.size());
int swap = A[i - 1];
A[i - 1] = A[math];
A[math] = swap;
}
}
无序向量
元素及相关操作
*访问
- 区间删除

public static int[] remove(int[] arr,int lo,int hi) { //删除数组中某一元素方法
while(hi < arr.length - 1){
arr[++lo] = arr[++hi];
}
arr = Arrays.copyOf(arr, arr.length-(hi - lo)); //减小数组长度
return arr;
}
无序向量的查找
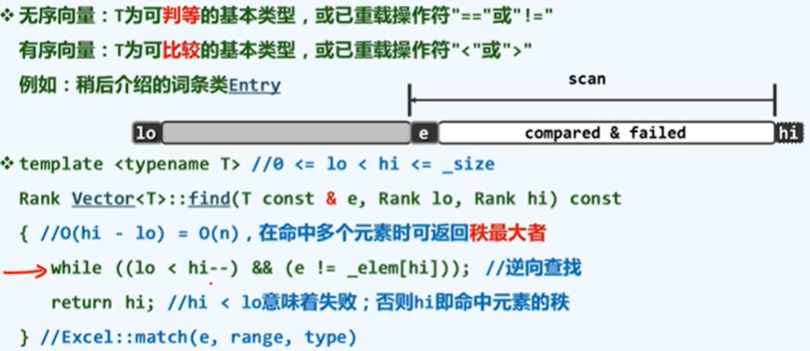
public int find(Object e , int lo, int hi, Object[] _elem){
while(( lo < hi--)&&(e != _elem[hi]));
return hi;//若hi < lo,则意味着失败;否则hi即命中元素的秩
}
public int remove(int lo, int hi, Object[] _elem){
if ( lo == hi){
return 0;
}
while( hi < _elem.length){
_elem[lo++] = _elem[hi++];
}
//shrink();
return hi - lo;
}
无序向量的唯一化

public int deduplicate(int _size ,Object[] _elem){
int oldsize = _size;
int i = 1;
while(i < _size){
(find(_elem[i],0,i,_elem)) ? i++ : remove(i);
}
return oldsize - _size;
}
遍历

@Test
public void test3(){
Vector<String> t=new Vector<String>();
t.add("F");
t.add("o");
t.add("r");
t.add("e");
t.add("v");
t.add("e");
t.add("r");
//第一种
for (String string : t) {
System.err.print(string);
}
//第二种
t.forEach(new Consumer<String>() {
@Override
public void accept(String t) {
// TODO Auto-generated method stub
System.out.print(t);
}
});
//第三种
for (int i = 0; i < t.size(); i++) {
System.out.print(t.get(i));
}
//第四种
Iterator<String> it = t.iterator();
while (it.hasNext()) {
String string = (String) it.next();
System.err.print(string);
}
//第五种
Enumeration<String> enume = t.elements();
while(enume.hasMoreElements()){
System.out.print(enume.nextElement().toString());
}
}
有序向量:唯一性
有序程度

@Test
public int test1(){
int[] _elem = new int[]{1,5,6,9,12,63,2,49,31,67};
int n = 0;
for (int i = 1;i < _elem.length;i++){
if (_elem[i -1] > _elem[i]){
n++;
}
}
return n;
}
低效版

@Test
public void test2(){
int[] _elem = new int[]{1,5,5,5,6,9,9,9,31,49,49,52,63};
int oldsize = _elem.length;
int i = 0;
while(i < _elem.length - 1){
if (_elem[i] == _elem[i+1]){
_elem = remove(_elem,i,i+1);
}else {
i++;
}
}
System.out.println(Arrays.toString(_elem));
System.out.println(oldsize - _elem.length);
}
public static int[] remove(int[] arr,int lo,int hi) { //删除数组中某一元素方法
while(hi < arr.length - 1){
arr[++lo] = arr[++hi];
}
arr = Arrays.copyOf(arr, arr.length-(hi - lo)); //减小数组长度
return arr;
}
高效办
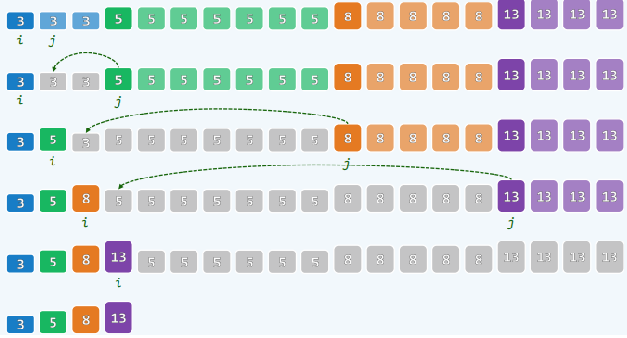

@Test
public void test3(){
int[] _elem = new int[]{1,5,5,5,6,9,9,9,31,49,49,52,63};
int i = 0;
int j = 0;
int oldsize = _elem.length;
while (++j < _elem.length){
if (_elem[i] != _elem[j]){
_elem[++i] = _elem[j];
}
}
_elem = remove(_elem, i,oldsize - 1);
System.out.println(Arrays.toString(_elem));
System.out.println(oldsize - 1 -i);
}
有序向量:查找
二分法:简单版

@Test
public void test1(){
int[] _elem = new int[]{1,5,5,5,6,9,9,9,31,49,49,52,63};
int lo = 0;
int e = 32;
int hi = _elem.length;
int mi = find3(_elem,e,lo,hi);
System.out.println(mi);
}
//简单的二分法查找
public int find1(int[] S,int e,int lo,int hi){
while (lo < hi){
int mi = (lo + hi) >>1;
if (e < S[mi]){
hi = mi;
}else if (S[mi] < e){
lo = mi + 1;
}else {
return mi;
}
}
return -1;
}
二分法:不考虑轴点
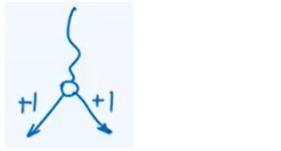
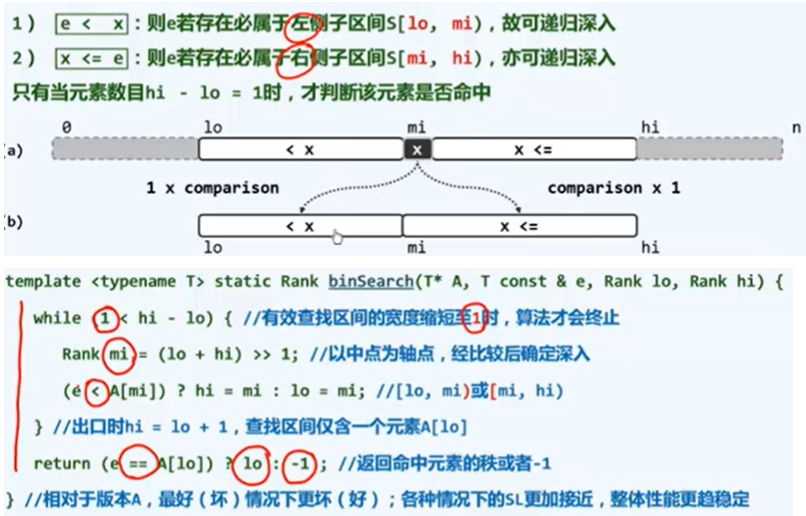
/**
* 二分法查找:不算轴点
*/
public int find(int[] S,int e,int lo,int hi){
while (1 < hi - lo){
int mi = (lo + hi) >>1;//取得两者的中点
if (e < S[mi]){//mi处值大于e
hi = mi;//令hi = mi
}else {//小于e
lo = mi;//令lo = mi
}//这里没有考虑相等的情况,把相等放在了右侧区间
}
if(S[lo] == e){
return lo;
}else {
return -1;
}
}
斐波那契查找
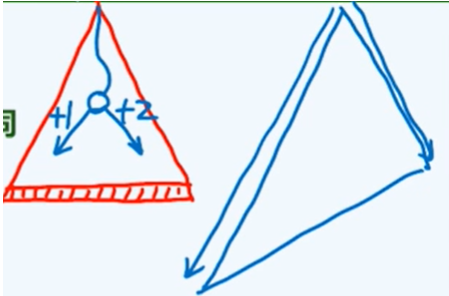
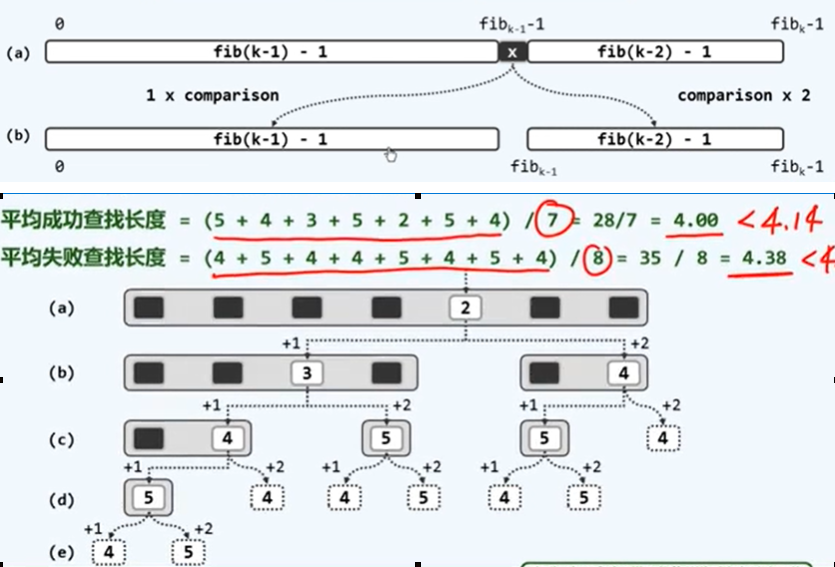
/**
* 斐波那契数列查找
* 向量的长度 n = fib(k) - 1,则可取mi = fib(k - 1) - 1,于是,前、后子向量的长度分别为
* fib(k-1)-1、 fib(k-2)-1;这里并不要求向量的长度一定要正好==fib(n) - 1;只要
* 用最小的n满足size<=fib(n) - 1即可
*/
public int find2(int[] S,int e,int lo,int hi){
while (lo < hi){
int n = 0;
while (hi - lo > fib(n) - 1){
n++;
}
int mi = lo + fib(n-1) - 1;
if (e < S[mi]){
hi = mi;
}else if (S[mi] < e){
lo = mi + 1;
}else {
return mi;
}
}
return -1;
}
public int fib(int n){
int f = 0;
int g = 1;
while(0 < n--){
g = g + f;
f = g - f;
}
return g;
}
插值查找
不一定每次都固定的选取 mi 相对于 lo 和 hi 的值,而是可以根据具体值来动态的确定 mi 。
二分查找 是对 n 的数值每次折半的话,那 插值查找 实际上是对 n 的二进制位宽度来做二分查找。二分查找的迭代次数,我们知道是 logn 的,而 长度是 logn 的,所以最后插值查找的迭代次数就是 loglogn 的。

public int find4(int[] S,int e,int lo,int hi){
while (lo < hi){
int mi = lo + (hi - lo)*(e - S[lo]) / (S[hi] - S[lo]);
if (e < S[mi]){
hi = mi;
}else if (S[mi] < e){
lo = mi + 1;
}else {
return mi;
}
}
return -1;
}

排序
起泡排序
- 简单版-考虑是否已经全部有序

@Test
public void test1(){
int[] _elem = {100, 836, 3236, 5, 16, 26, -3, 89, 69, 43};
int n = _elem.length;
sort4(_elem,0,n);
System.out.println(Arrays.toString(_elem));
}
/**
* 排列的时候考虑到过程中已经全部有序的情况,这里是n--
*/
public void sort1(int[] A,int n) {
for (boolean sorted = false; sorted = !sorted; n--) {
for (int i = 1; i < n; i++) {
if (A[i - 1] > A[i]) {
int b = A[i - 1];
A[i - 1] = A[i];
A[i] = b;
sorted = false;
}
}
}
}
- 改进1-考虑是否后方局部有序

/**
* 排列的时候针对乱序元素位于[0,根号n],考虑到过程中后方已经有序的情况,这里是n-很多
*/
public void sort2(int[] A,int lo,int hi) {
while (lo < (hi = bubble1(A,lo,hi)));
}
public int bubble1(int[] A,int lo,int hi){//一趟扫描
int last = lo;
while (++lo < hi){
if (A[lo - 1] > A[lo]) {
last = lo;
int b = A[lo - 1];
A[lo - 1] = A[lo];
A[lo] = b;
}
}
return last;
}
- 改进2-考虑是否前方局部有序

/**
* 排列的时候针对乱序元素位于[n-根号n,n],考虑到过程中前方已经有序的情况,这里是n-很多
*/
public void sort3(int[] A,int lo,int hi) {
while ((lo = bubble2(A,lo,hi)) < hi );
}
public int bubble2(int[] A,int lo,int hi){//一趟扫描
int first = hi;
while (lo < --hi){
if (A[hi - 1] > A[hi]) {
first = hi - 1;
int b = A[hi - 1];
A[hi - 1] = A[hi];
A[hi] = b;
}
}
return first;
}
- 改进3-考虑前后不断排除有序情况

public void sort4(int[] A,int lo,int hi) {
while ((lo = bubble2(A,lo,hi)) < (hi = bubble1(A,lo,hi)) );
}
选择排序

public class choiceSort {
/**
* 选择排序
*/
@Test
public void test2(){
int [] arr = {49,38,65,97,76,13,27,49};
selectSort(arr,arr.length);
}
public void selectSort(int [] arr,int n){
for (int i = 0; i < n - 1; i++) {
int index = i;
int j;
// 找出最小值得元素下标
for (j = i + 1; j < n; j++) {
if (arr[j] < arr[index]) {
index = j;
}
}
int tmp = arr[index];
arr[index] = arr[i];
arr[i] = tmp;
}
}
}
归并排序
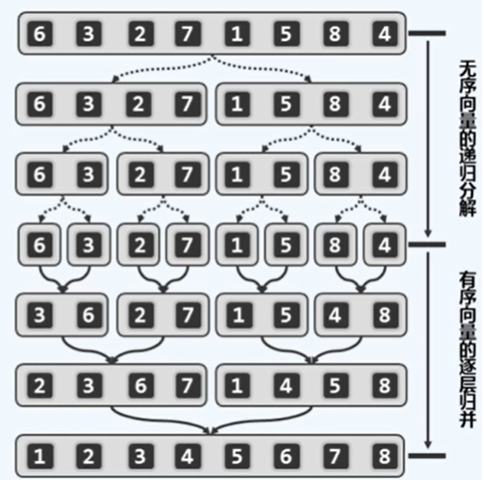

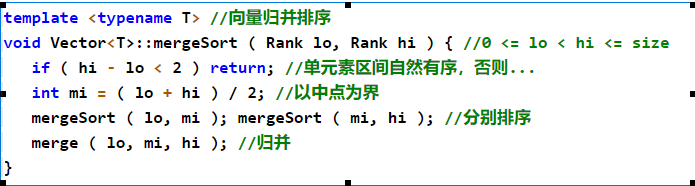

public class MergeSort {
public static void main(String []args){
int[] arr = {100, 836, 3236, 5, 16, 26, -3, 89, 69, 43};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
int []temp = new int[arr.length];//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
sort(arr,0,arr.length-1,temp);
}
private static void sort(int[] arr,int left,int right,int []temp){
if(left<right){
int mid = (left+right)/2;
sort(arr,left,mid,temp);//左边归并排序,使得左子序列有序
sort(arr,mid+1,right,temp);//右边归并排序,使得右子序列有序
merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
}
}
private static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;//左序列指针
int j = mid+1;//右序列指针
int t = 0;//临时数组指针
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while(j<=right){//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while(left <= right){
arr[left++] = temp[t++];
}
}
}