题目描述
小红很喜欢玩一个叫打砖块的游戏,这个游戏的规则如下:
在刚开始的时候,有n行*m列的砖块,小红有k发子弹。小红每次可以用一发子弹,打碎某一列当前处于这一列最下面的那块砖,并且得到相应的得分。(如图所示)
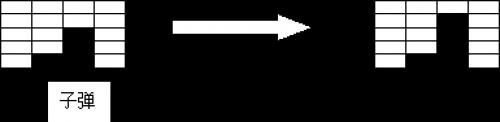
某些砖块在打碎以后,还可能将得到一发子弹的奖励。最后当所有的砖块都打碎了,或者小红没有子弹了,游戏结束。
小红在游戏开始之前,就已经知道每一块砖在打碎以后的得分,并且知道能不能得到一发奖励的子弹。小红想知道在这次游戏中她可能的最大得分,可是这个问题对于她来说太难了,你能帮帮她吗?
输入输出格式
输入格式:
第一行有3个正整数,n,m,k。表示开始的时候,有n行*m列的砖块,小红有k发子弹。
接下来有n行,每行的格式如下:
f1 c1 f2 c2 f3 c3 …… fm cm
其中fi为正整数,表示这一行的第i列的砖,在打碎以后的得分。ci为一个字符,只有两种可能,Y或者N。Y表示有一发奖励的子弹,N表示没有。
所有的数与字符之间用一个空格隔开,行末没有多余的空格。
输出格式:
仅一个正整数,表示最大的得分。
输入输出样例
输入样例#1:
3 4 2
9 N 5 N 1 N 8 N
5 N 5 Y 5 N 5 N
6 N 2 N 4 N 3 N
输出样例#1:
13
说明
对于20%的数据,满足1<=n,m<=5,1<=k<=10,所有的字符c都为N
对于50%的数据,满足1<=n,m<=200,1<=k<=200,所有的字符c都为N
对于100%的数据,满足1<=n,m<=200,1<=k<=200,字符c可能为Y
对于100%的数据,所有的f值满足1<=f<=10000
啊啊啊啊啊!!
深奥的DP
看的题解,也没怎么看懂、、、日后再回来看看
1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 #include<vector> 7 using namespace std; 8 const int mxn=220; 9 int read(){ 10 int x=0,f=1;char ch=getchar(); 11 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 12 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 13 return x*f; 14 } 15 int f1[mxn][mxn],f2[mxn][mxn];//[列][使用子弹数]=最优解 16 int n,m,k; 17 int mp[mxn][mxn]; 18 bool re[mxn][mxn]; 19 int w1[mxn][mxn],w2[mxn][mxn]; 20 void init(){ 21 for(int j=1;j<=m;j++){ 22 int cnt=n; 23 while(cnt && re[cnt][j]){ 24 w1[j][0]+=mp[cnt][j]; 25 cnt--; 26 } 27 for(int i=1;i<=n && cnt ;i++){//打了i发子弹 28 w2[j][i]=w1[j][i-1]+mp[cnt][j]; 29 w1[j][i]=w2[j][i]; 30 cnt--; 31 while(cnt && re[cnt][j]){ 32 w1[j][i]+=mp[cnt][j]; 33 cnt--; 34 } 35 } 36 } 37 return; 38 } 39 int main(){ 40 n=read();m=read();k=read(); 41 int i,j; 42 for(i=1;i<=n;i++) 43 for(j=1;j<=m;j++){ 44 mp[i][j]=read(); 45 char ch=getchar(); 46 if(ch=='N')re[i][j]=0; 47 else re[i][j]=1; 48 } 49 init(); 50 /* 51 for(i=1;i<=n;i++){ 52 for(j=1;j<=m;j++){ 53 printf("%5d %5d ",mp[i][j],num[i][j]); 54 } 55 printf(" "); 56 }*/ 57 for(i=1;i<=m;i++){//列 58 for(j=0;j<=k;j++){//子弹 59 for(int l=0;l<=j;l++){//之前已用子弹 60 f1[i][j]=max(f1[i][j],f1[i-1][j-l]+w1[i][l]); 61 if(l<j){ 62 f2[i][j]=max(f2[i][j],f2[i-1][j-l]+w1[i][l]); 63 } 64 if(l){ 65 f2[i][j]=max(f2[i][j],f1[i-1][j-l]+w2[i][l]); 66 } 67 } 68 } 69 } 70 printf("%d ",f2[m][k]); 71 return 0; 72 }