Codevs 3269 混合背包

3269 混合背包

  时间限制: 1 s　　　　空间限制: 256000 KB　　　　题目等级 : 钻石 Diamond

题目描述 Description

背包体积为V ,给出N个物品，每个物品占用体积为Vi,价值为Wi,每个物品要么至多取1件，要么至多取mi件（mi > 1） , 要么数量无限 ， 在所装物品总体积不超过V的前提下所装物品的价值的和的最大值是多少？

输入描述 Input Description

第一行两个数N,V,下面N行每行三个数Vi,Wi,Mi表示每个物品的体积，价值与数量，Mi=1表示至多取一件，Mi>1表示至多取Mi件，Mi=-1表示数量无限

输出描述 Output Description

1个数Ans表示所装物品价值的最大值

样例输入 Sample Input

2 10

3 7 2

2 4 -1

样例输出 Sample Output

22

数据范围及提示 Data Size & Hint

对于100%的数据,V <= 200000 , N <= 200

// 混合背包板子  我的哥 全TLE~~~~~~~~ 
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define N 210
#define V 200010
int n,v,f[V],wi[N],mi[N],vi[N];
int main() 
{
    scanf("%d%d",&n,&v);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",&vi[i],&wi[i],&mi[i]);
        if(mi[i]==-1) mi[i]=v/vi[i];
    }
    for(int i=1;i<=n;i++)
    {
        for(int k=1;k<=mi[i];k++)
        {
            for(int j=v;j>=vi[i];j--)
              f[j]=max(f[j],f[j-vi[i]]+wi[i]);
        }
    }
    printf("%d",f[v]);
    return 0;
}

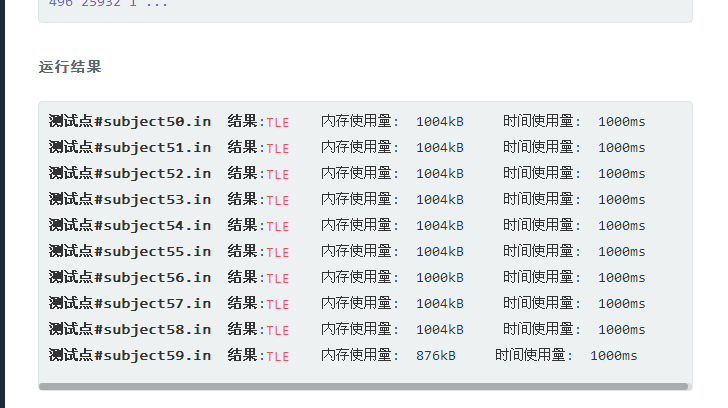
AC代码：

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define N 210
#define V 200010
int n,v,f[V],wi[N],mi[N],vi[N];
int main() 
{
    scanf("%d%d",&n,&v);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",&vi[i],&wi[i],&mi[i]);
        if(mi[i]==-1) mi[i]=v/vi[i];
    }
    for(int i=1;i<=n;i++)
    {
        int x=mi[i];
        for(int k=1;k<=x;k<<=1)//二分制优化   
        {
            for (int j=v;j>=vi[i]*k;j--)
                f[j]=max(f[j],f[j-vi[i]*k]+wi[i]*k); 
            x-=k;   
        }
      if(x)
        for (int j=v;j>=vi[i]*x;j--)
          f[j]=max(f[j],f[j-vi[i]*x]+wi[i]*x);
    }
    printf("%d",f[v]);
    return 0;
}

再次说明一点，我将可以去无数次的物品的次数换成了v/vi[i]次（即通过总背包体积来限制他，这样就可以省掉一步）。。。

二进制优化~~~依然的慢

待解救~~~~~~~

还有这题和队列有个毛关系~~