图是由有穷非空集合的顶点和顶点之间的边组成的集合,通常表示为G(V,E),其中G表示一个图,V表示图G中的顶点的集合,E是图G中边的集合。
- 在线性结构中,每个元素都只有一个直接前驱和一个直接后继,主要用来表示一对一的数据结构。
- 在树形结构中,数据之间有着明显的父子关系,主要用来表示一对多的数据结构。
- 在图形结构中,数据之间具有任意关系,图中任意两个数据之间都可能相关,主要用来表示多对多的数据结构。
1、图的表示方式(存储结构)
图的表示方式有两种:邻接矩阵和邻接表。
1.1邻接矩阵
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于n个顶点的图而言,矩阵的行和列表示1~n个点。
无向图的邻接矩阵,如图:
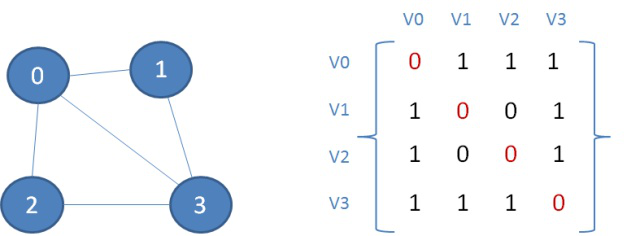
有向图的邻接矩阵,如图:
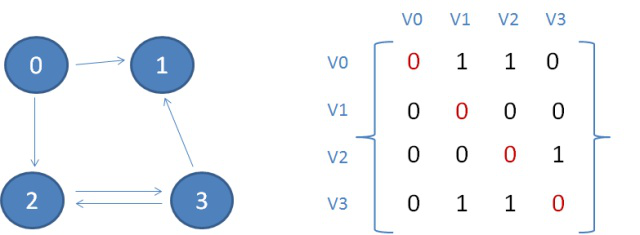
带权图的邻接矩阵,如图:
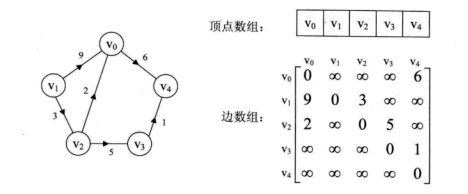
1.2 邻接表
邻接表是指数组和链表相结合的存储方式。邻接表是图的一种链式存储结构,主要解决邻接矩阵中顶点多而边少时浪费空间的问题。
无向图的邻接表,如图:
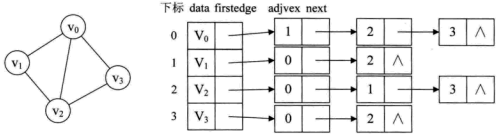
带权图的邻接表,如图:

data:数据,存储顶点的信息;
firstedge:指针域,指向边表的第一个结点,即此顶点的第一个邻接点;
adjvex:邻接点域,存储某顶点的邻接点在顶点表中的下标;
weight:权重;
next:存储指向边表中下一个结点的指针。
1.3 图的代码实现
(1)实现图的数据结构:
public class Graph { private ArrayList<String> vertexList;//存储顶点集合 private int[][] edges;//存储图对应的邻接矩阵 private int numOfEdges;//图中边的数目 //构造器 public Graph(int n) { edges = new int[n][n]; vertexList = new ArrayList<String>(n); numOfEdges = 0; } //插入顶点 public void insertVertex(String vertex){ vertexList.add(vertex); } //插入有关系边(A-B,B-C....) public void insertEdge(int v1,int v2, int weight){ edges[v1][v2] = weight; edges[v2][v1] = weight; numOfEdges++; } //获得边的数目 public int getNumOfEdges(){ return numOfEdges; } //获得结点个数 public int getVertexList() { return vertexList.size(); } //显示图对应的矩阵 public void showGraph(){ for (int[] link:edges){ System.out.println(Arrays.toString(link)); } } }
(2)实现图:
//实现图: // A B C D E //A 0 1 1 0 0 //B 1 0 1 1 1 //C 1 1 0 0 0 //D 0 1 0 0 0 //E 0 1 0 0 0 public class Main { public static void main(String[] args) { int n = 5; String vertexs[] = {"A", "B", "C", "D", "E"}; Graph graph = new Graph(n); for (String vertex : vertexs) { graph.insertVertex(vertex); } //添加边 graph.insertEdge(0,1,1); graph.insertEdge(0,2,1); graph.insertEdge(1,2,1); graph.insertEdge(1,3,1); graph.insertEdge(1,4,1); graph.showGraph(); } }
1.4 图的遍历
图的遍历指从图中某一顶点出发访遍图中的每个顶点,且使每一个顶点仅被访问一次。图的遍历分为广度优先遍历和深度优先遍历,对无向图和有向图都适用。
1、深度优先
图的深度优先搜索,和树的先序遍历比较类似。
原图:
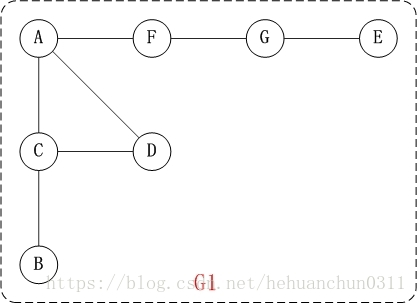
深度优先遍历,如图:
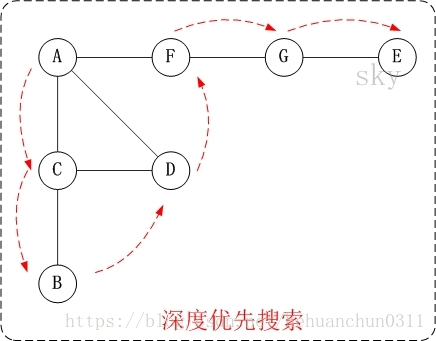
访问顺序是:A -> C -> B -> D -> F -> G -> E
2、广度优先
广度优先遍历,类似于树的分层遍历算法。
广度优先遍历,如图:
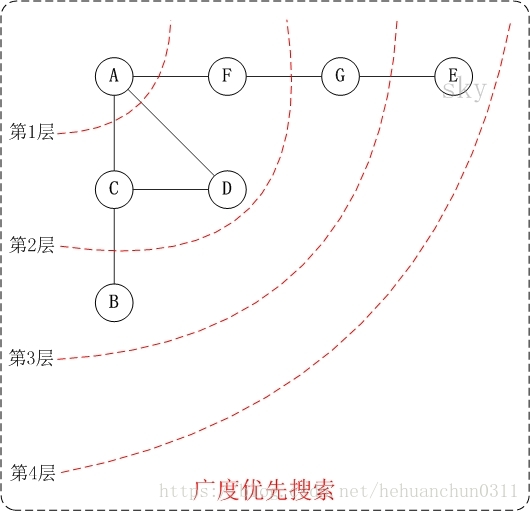
访问顺序是:A -> C -> D -> F -> B -> G -> E
1.5 位图
位图(bitmap)通常基于数组实现。就是用每一位来存放某种状态,适用于大规模数据,但数据状态又不是很多的情况。通常是用来判断某个数据存不存在的。
位图在内部维护了一个M*N维的数组char[M][N],在这个数组里面每个字节占8位,因此可以存储M*N*8个数据。
例如要存储的数据范围为0~15,只需分配使用M=1,N=2的数据进行存储,具体的数据结构,如图:

数据为【5,1,7,15,0,4,6,10】,则存入这个结构中的情况为,如图:
