目录
1052.Tian Ji -- The Horse Racing
1045 Fire Net
Suppose that we have a square city with straight streets. A map of a city is a square board with n rows and n columns, each representing a street or a piece of wall.
A blockhouse is a small castle that has four openings through which to shoot. The four openings are facing North, East, South, and West, respectively. There will be one machine gun shooting through each opening.
Here we assume that a bullet is so powerful that it can run across any distance and destroy a blockhouse on its way. On the other hand, a wall is so strongly built that can stop the bullets.
The goal is to place as many blockhouses in a city as possible so that no two can destroy each other. A configuration of blockhouses is legal provided that no two blockhouses are on the same horizontal row or vertical column in a map unless there is at least one wall separating them. In this problem we will consider small square cities (at most 4x4) that contain walls through which bullets cannot run through.
The following image shows five pictures of the same board. The first picture is the empty board, the second and third pictures show legal configurations, and the fourth and fifth pictures show illegal configurations. For this board, the maximum number of blockhouses in a legal configuration is 5; the second picture shows one way to do it, but there are several other ways. 
Your task is to write a program that, given a description of a map, calculates the maximum number of blockhouses that can be placed in the city in a legal configuration.
Input
The input file contains one or more map descriptions, followed by a line containing the number 0 that signals the end of the file. Each map description begins with a line containing a positive integer n that is the size of the city; n will be at most 4. The next n lines each describe one row of the map, with a '.' indicating an open space and an uppercase 'X' indicating a wall. There are no spaces in the input file.
Output
For each test case, output one line containing the maximum number of blockhouses that can be placed in the city in a legal configuration.
Sample Input
4
.X..
....
XX..
....
2
XX
.X
3
.X.
X.X
.X.
3
...
.XX
.XX
4
....
....
....
....
0
Sample Output
5
1
5
2
4
#include<iostream>
#include<cstdio>
using namespace std;
int ans;
char s[5][5];
int n;
int c_put(int n,int m)
{
for(int i=n-1;i>=0;i--)
{
if(s[i][m]=='0')
return 0;
if(s[i][m]=='X')
break;
}
for(int j=m-1;j>=0;j--)
{
if(s[n][j]=='0')
return 0;
if(s[n][j]=='X')
break;
}
return 1;
}
void dfs(int k,int num)
{
int x,y;
if(k==n*n)
{
if(num>ans)
ans=num;
return ;
}
else
{
x=k/n;
y=k%n;
if(s[x][y]=='.'&&c_put(x,y))
{
s[x][y]='0';
dfs(k+1,num+1);
s[x][y]='.';
}
dfs(k+1,num);
}
}
int main()
{
while(~scanf("%d",&n)&&n)
{
ans=0;
for(int i=0;i<n;i++)
{
getchar();
for(int j=0;j<n;j++)
scanf("%c",&s[i][j]);
}
dfs(0,0);
printf("%d
",ans);
}
}1050.Moving Tables
The famous ACM (Advanced Computer Maker) Company has rented a floor of a building whose shape is in the following figure.

The floor has 200 rooms each on the north side and south side along the corridor. Recently the Company made a plan to reform its system. The reform includes moving a lot of tables between rooms. Because the corridor is narrow and all the tables are big, only one table can pass through the corridor. Some plan is needed to make the moving efficient. The manager figured out the following plan: Moving a table from a room to another room can be done within 10 minutes. When moving a table from room i to room j, the part of the corridor between the front of room i and the front of room j is used. So, during each 10 minutes, several moving between two rooms not sharing the same part of the corridor will be done simultaneously. To make it clear the manager illustrated the possible cases and impossible cases of simultaneous moving.

For each room, at most one table will be either moved in or moved out. Now, the manager seeks out a method to minimize the time to move all the tables. Your job is to write a program to solve the manager’s problem.
Input
The input consists of T test cases. The number of test cases ) (T is given in the first line of the input. Each test case begins with a line containing an integer N , 1<=N<=200 , that represents the number of tables to move. Each of the following N lines contains two positive integers s and t, representing that a table is to move from room number s to room number t (each room number appears at most once in the N lines). From the N+3-rd line, the remaining test cases are listed in the same manner as above.
Output
The output should contain the minimum time in minutes to complete the moving, one per line.
Sample Input
3
4
10 20
30 40
50 60
70 80
2
1 3
2 200
3
10 100
20 80
30 50
Sample Output
10
20
30
#include <iostream>
using namespace std;
struct table{
int front,back;
bool use;
}tb[10001];
int main()
{
int T,N,total; //T为有几组数据,N为每组数据有几行数据,total为总用时
int i,j,temp;
table tem;
cin>>T;
while(T--)
{
//************************** 输入
cin>>N;
for(i=0;i<N;++i)
{
cin>>tb[i].front>>tb[i].back;
if(tb[i].front%2==1)
tb[i].front+=1;
if(tb[i].back%2==1)
tb[i].back+=1;
if(tb[i].front>tb[i].back)
{
temp=tb[i].front;
tb[i].front=tb[i].back;
tb[i].back=temp;
}
tb[i].use=true;
}
//************************* 排序
for(i=0;i<N-1;++i)
for(j=N-1;j>i;--j)
if(tb[i].front>tb[j].front)
{
tem=tb[i];
tb[i]=tb[j];
tb[j]=tem;
}
//************************* 计算值
total=0;
for(i=0;i<N;++i)
{
if(tb[i].use==false)
continue;
temp=tb[i].back;
for(j=i+1;j<N;++j)
{
if(tb[j].use==false)
continue;
if(tb[j].front>temp)
{
tb[j].use=false;
temp=tb[j].back;
}
}
total+=10;
}
//************************* 输出
cout<<total<<endl;
}
return 0;
}
/*
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int cnt[200];
bool cmp(int a,int b)
{
return a>b;
}
int main()
{
int T,n,a,b,l,r;
scanf("%d",&T);
while(T--)
{
memset(cnt,0,sizeof(cnt));
scanf("%d",&n);
for(int i=0;i<n;++i)
{
scanf("%d%d",&a,&b);
l=min(a,b);
r=max(a,b);
l=(l+1)/2;
r=(r+1)/2;
for(int j=l;j<=r;++j)
cnt[j]++;
}
sort(cnt,cnt+200,cmp);
printf("%d
",cnt[0]*10);
}
return 0;
}
*/1051.Wooden Sticks
There is a pile of n wooden sticks. The length and weight of each stick are known in advance. The sticks are to be processed by a woodworking machine in one by one fashion. It needs some time, called setup time, for the machine to prepare processing a stick. The setup times are associated with cleaning operations and changing tools and shapes in the machine. The setup times of the woodworking machine are given as follows:
(a) The setup time for the first wooden stick is 1 minute.
(b) Right after processing a stick of length l and weight w , the machine will need no setup time for a stick of length l' and weight w' if l<=l' and w<=w'. Otherwise, it will need 1 minute for setup.
You are to find the minimum setup time to process a given pile of n wooden sticks. For example, if you have five sticks whose pairs of length and weight are (4,9), (5,2), (2,1), (3,5), and (1,4), then the minimum setup time should be 2 minutes since there is a sequence of pairs (1,4), (3,5), (4,9), (2,1), (5,2).
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case consists of two lines: The first line has an integer n , 1<=n<=5000, that represents the number of wooden sticks in the test case, and the second line contains n 2 positive integers l1, w1, l2, w2, ..., ln, wn, each of magnitude at most 10000 , where li and wi are the length and weight of the i th wooden stick, respectively. The 2n integers are delimited by one or more spaces.
Output
The output should contain the minimum setup time in minutes, one per line.
Sample Input
3
5
4 9 5 2 2 1 3 5 1 4
3
2 2 1 1 2 2
3
1 3 2 2 3 1
Sample Output
2
1
3
#include <stdio.h>
#include <algorithm>
struct st {
int l, w, vis;
bool operator<(const st&c)const {
return l==c.l?w<c.w:l<c.l;
}
}stick[5001];
int n;
void read() {
scanf("%d", &n);
for(int i=0; i<n; i++) {
scanf("%d%d", &stick[i].l, &stick[i].w);
stick[i].vis = 0;
}
}
void find(int i) {
int k = i;
for(int j=i+1; j<n; j++)
if(!stick[j].vis)
if(stick[k].w<=stick[j].w) {
stick[j].vis = 1;
k=j;
}
}
void work() {
int res = 0;
std::sort(stick, stick+n);
for(int i=0; i<n; i++) {
if(!stick[i].vis) {
stick[i].vis = 1;
++res;
find(i);
}
}
printf("%d
", res);
}
int main() {
int T, n;
scanf("%d", &T);
while(T--) {
read();
work();
}
return 0;
}
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
struct Node
{
int l,w;
}node[5005],setup[5005];
bool cmp(Node a,Node b)
{
if(a.l==b.l)
return a.w<b.w;
return a.l<b.l;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n,i,j;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>node[i].l>>node[i].w;
}
sort(node,node+n,cmp);
int ans=1;
setup[0].l=node[0].l;
setup[0].w=node[0].w;
for(i=1;i<n;i++)
{
int ok=0;
for(j=0;j<ans;j++)
{
if(setup[j].l<=node[i].l&&setup[j].w<=node[i].w)
{
setup[j].l=node[i].l;
setup[j].w=node[i].w;
ok=1;
break;
}
}
if(ok==0)
{
setup[ans].l=node[i].l;
setup[ans].w=node[i].w;
ans++;
}
}
cout<<ans<<endl;
}
return 0;
}//自己写的
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
struct Node
{
int l,w,vis;
}node[5005],setup[5005];
bool cmp(Node a,Node b)
{
if(a.l==b.l)
return a.w<b.w;
return a.l<b.l;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>node[i].l>>node[i].w;
node[i].vis=0;
}
sort(node,node+n,cmp);
int ans=0,flag;
for(int i=0;i<n;i++)
{
if(node[i].vis)
continue;
if(!node[i].vis)
{
ans++;
}
int k=node[i].w;
for(int j=i+1;j<n;j++)
{
if(k<=node[j].w&&!node[j].vis)
{
k=node[j].w;
node[j].vis=1;
}
}
}
cout<<ans<<endl;
}
return 0;
}1052.Tian Ji -- The Horse Racing
Here is a famous story in Chinese history.
"That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others."
"Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser."
"Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian's. As a result, each time the king takes six hundred silver dollars from Tian."
"Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match."
"It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king's regular, and his super beat the king's plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?"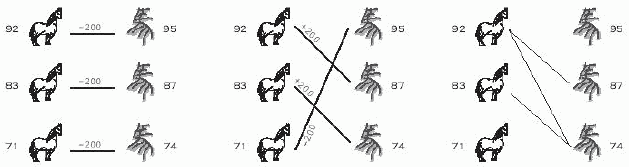
Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian's horses on one side, and the king's horses on the other. Whenever one of Tian's horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching...
However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses --- a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.
In this problem, you are asked to write a program to solve this special case of matching problem.
Input
The input consists of up to 50 test cases. Each case starts with a positive integer n (n <= 1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian’s horses. Then the next n integers on the third line are the speeds of the king’s horses. The input ends with a line that has a single 0 after the last test case.
Output
For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.
Sample Input
3
92 83 71
95 87 74
2
20 20
20 20
2
20 19
22 18
0
Sample Output
200
0
0
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int a[1010],b[1010];
int main()
{
int n,awin,bwin,afast,bfast,aslow,bslow;
while(scanf("%d",&n)&&n)
{
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
for(int i=0;i<n;i++)
scanf("%d",&b[i]);
sort(a,a+n);
sort(b,b+n);
awin=bwin=0;
afast=bfast=n-1;
aslow=bslow=0;
for(int i=0;i<n;i++)
{
if(a[aslow]>b[bslow])
{
awin++;
aslow++;
bslow++;
}
else if(a[aslow]<b[bslow])
{
bwin++;
aslow++;bfast--;
}
else{
if(a[afast]>b[bfast])
{
awin++;
afast--;bfast--;
}
else if(a[aslow]<b[bfast])
{
bwin++;
aslow++;bfast--;
}
}
}
cout<<200*(awin-bwin)<<endl;
}
return 0;
}