1373D. Maximum Sum on Even Positions
题意
给定一个下标从0开始的数列
最多旋转一次子数列(将某一段子数列倒置)
问所有偶数位置上的元素和的最大值
限制
Time limit per test: 2 seconds
Memory limit per test: 256 megabytes
1≤t≤2⋅104
1≤n≤2⋅105
1≤ai≤109
∑n≤2⋅105
解
先求出偶数位置上元素和(初值)
可以发现,只有当选中的子数列长度为偶数时才能改变偶数位置上元素和(与奇数位置互换)
因为只涉及到奇偶交换,位置的奇偶性是固定的
所以可以直接看作将某一偶数长度段中,第一个元素与第二个元素互换,第三个与第四个互换,以此类推……
如下图所示
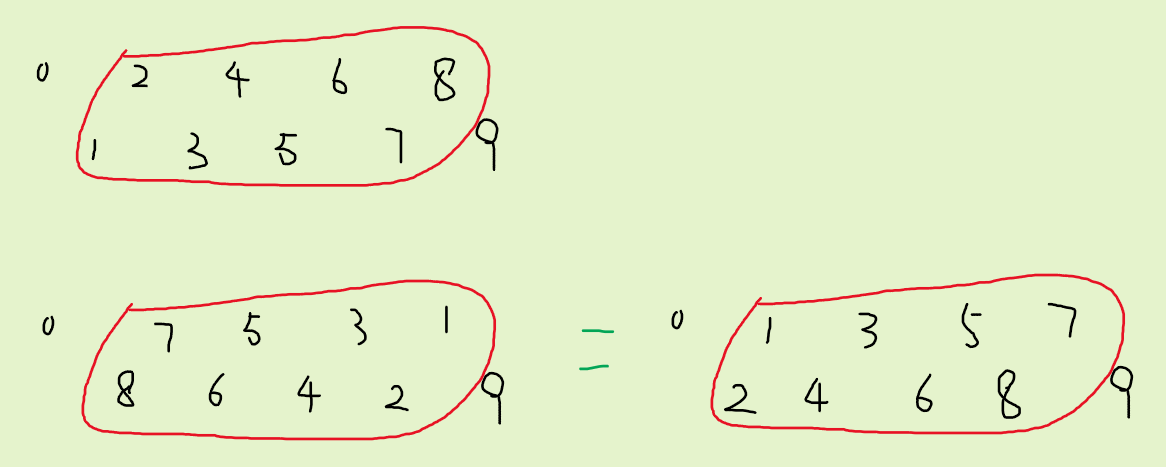
如果要替换原位置为 2 4 6 8 的元素,则只存在两种方案
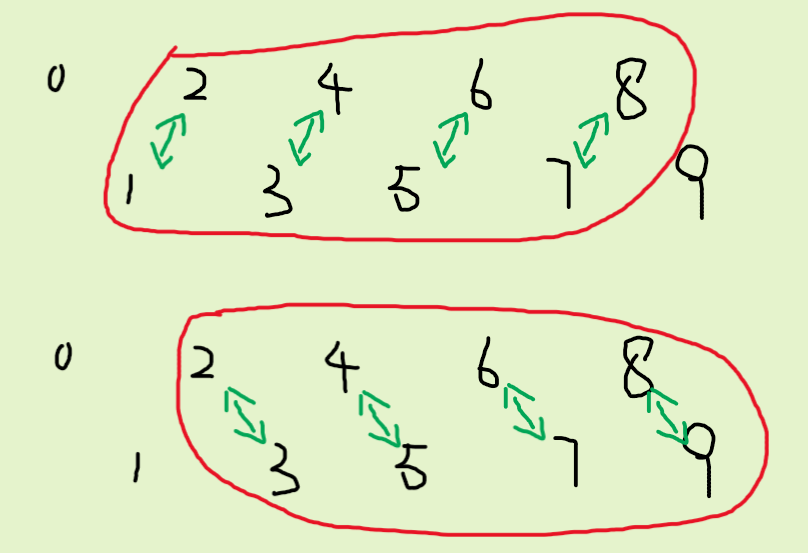
对于每种方案,在原数列中以每两个为一组,以奇数位-偶数位为值
求出最大连续子段和即为替换所能带来的最大收益
加上原本偶数位之和,即为答案
完整程序
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[200050];
void solve()
{
int n;
scanf("%d",&n);
ll ans=0;
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
if((i&1)==0)
ans+=a[i]; //原偶数位之和
}
ll tmp1=0,tmp2=0,mx=0;
for(int i=0;i<n;i+=2)
{
if(i+1<n) //用i+1替换i
{
tmp1+=a[i+1]-a[i];
mx=max(mx,tmp1); //取大
if(tmp1<0) //连续子段最大和,如果和小于0,则从0开始计算
tmp1=0;
}
if(i>1) //用i-1替换i
{
tmp2+=a[i-1]-a[i];
mx=max(mx,tmp2);
if(tmp2<0)
tmp2=0;
}
}
printf("%lld
",ans+mx);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
solve();
return 0;
}