题:https://ac.nowcoder.com/acm/contest/5668/D
题意:给定n和m,要求你在全白的二维坐标上点上n个黑点,要求相邻颜色互异的点对恰好为m对(点x和点y,点y和点x被认为是相同的点对)。
分析:这题很容易想到一些限制条件:
1、n个黑点最多构成4n对点对,也就是m的上界为4*m;
2、m只能为偶数,可以假设一开始n个黑点构成4n点对,要让点对减少只能黑点与黑点相邻建,而这种方法消去的点对数是相互的,也就是一定是偶数。
关键是确立下界:
1、可以想象,n个黑点要构成尽可能小的点对肯定是全部“凑”在一起;
2、而由下图,俩图的点对都是14,也就是其周长2*(a+b),由此,因为周长一定,所以我们把n个点尽可能地“塞”成(a+b)较小的情况,这部分可直接暴力解决,得下界2*(a+b)

接着是构造:
1、由下界确定的步骤,我们可以一开始就把n个点设成下界,从上到下,从左到右。然后依次“挑出黑点”让其“孤立”。
2、而“挑出黑点”的过程点对减少有2种情况:
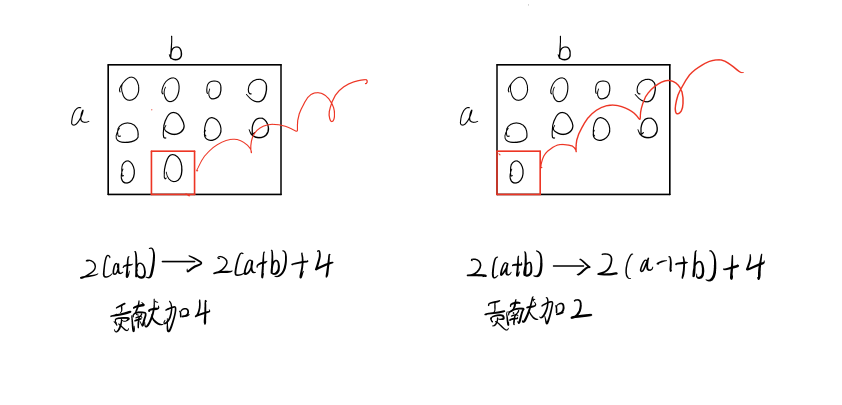
3、构造的过程就是“挑出黑点”的过程,最后只需将原本的和挑出的部分输出即为答案。

#include<bits/stdc++.h> using namespace std; #define pb push_back #define MP make_pair #define pii pair<int,int> typedef long long ll; typedef unsigned long long ull; const int mod=998244353; const int inf=0x3f3f3f3f; const ll INF=1e18; vector<pii>ans1,ans2; int main(){ int T; scanf("%d",&T); while(T--){ int n,m,a,b,minn=inf; ans1.clear(),ans2.clear(); scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) for(int j=1;j<=m;j++) if(i*j>=n&&(i-1)*j<n&&i*(j-1)<n){///要n个点能填充的矩形 if(2*(i+j)<minn){ minn=2*(i+j); a=i,b=j; } } if(m&1||m>4*n||m<minn){ puts("No"); continue; } for(int i=1;i<=a;i++) for(int j=1;j<=b;j++){ if(n==0) break; ans1.pb(MP(i,j)); n--; } int now=minn;///当前点对 int nowx=1000,nowy=1000; while(ans1.size()>1&&m>=now+4){ pii tmp=ans1.back(); ans1.pop_back(); if(tmp.first==1||tmp.second==1) now+=2; else now+=4; ans2.pb(MP(nowx,nowy)); nowx+=2; } if(m==now+2){ pii tmp=ans1.back(); ans1.pop_back(); if(tmp.first==1||tmp.second==1) ans2.pb(MP(nowx,nowy)); else ans2.pb(MP(tmp.first-1,b+1));///把贡献4的黑点拉到ans1的右侧,使其贡献为2 } puts("Yes"); for(auto it:ans1) printf("%d %d ",it.first,it.second); for(auto it:ans2) printf("%d %d ",it.first,it.second); } return 0; }
