在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。

㈠:二进制转十进制
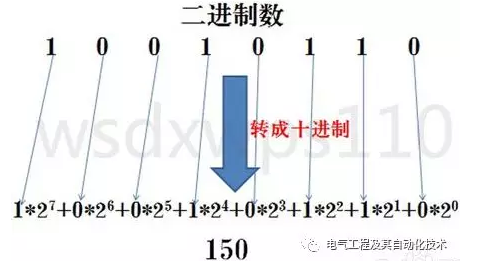
㈡十进制转二进制
方法为:用2整除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为小于1时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。具体如下图所示:

㈢二进制转八进制
二进制数转换成八进制数:从小数点开始,整数部分向左、小数部分向右,每3位为一组用一位八进制数的数字表示,不足3位的要用“0”补足3位,就得到一个八进制数。
(具体用法如下图)
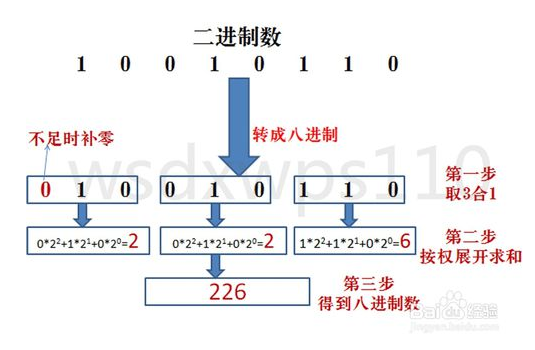
㈣:八进制转成二进制
八进制转换成二进制数:八进制数通过除2取余法,得到二进制数,每个八进制对应三个二进制,不足时在最左边补充零。
(具体用法如下图)

方法为:与二进制转八进制方法近似,八进制是取三合一,十六进制是取四合一。(注意事项,4位二进制转成十六进制是从右到左开始转换,不足时补0)。
(具体用法如下图)
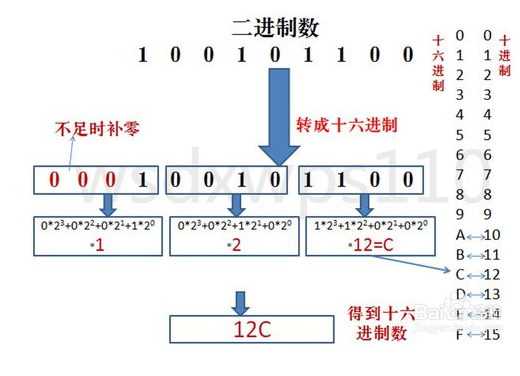
㈥十六进制转二进制
十六进制转二进制:十六进制数通过除2取余法,得到二进制数,每个十六进制对应四个二进制,不足时在最左边补充零。
(具体用法如下图)
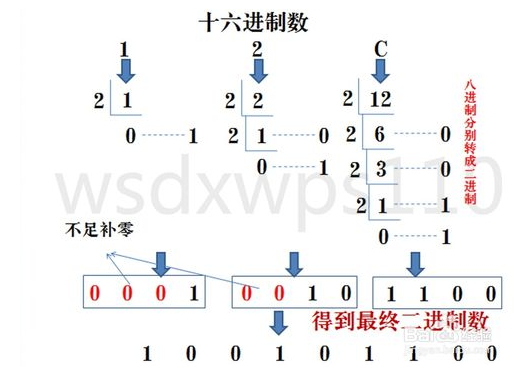
(七)、十进制转八进制或者十六进制有两种方法
第一:间接法—把十进制转成二进制,然后再由二进制转成八进制或者十六进制。这里不再做图片用法解释。
第二:直接法—把十进制转八进制或者十六进制按照除8或者16取余,直到商为0为止。

(八)、八进制或者十六进制转成十进制
方法为:把八进制、十六进制数按权展开、相加即得十进制数。

十六进制与八进制之间的转换
八进制与十六进制之间的转换有两种方法
第一种:他们之间的转换可以先转成二进制然后再相互转换。
第二种:他们之间的转换可以先转成十进制然后再相互转换。
这里就不再进行图片用法解释。
负数
负数的进制转换稍微有些不同。
先把负数写为其补码形式(在此不议),然后再根据二进制转换其它进制的方法进行。
例:要求把-9转换为八进制形式。则有:
-9的补码为1111 1111 1111 0111。从后往前三位一划,不足三位的加0111---->7
110---->6
111---->7
111---->7
111---->7
001---->1
然后我们将结果按从下往上的顺序书写就是:177767,那么177767就是十进制数-9的八进制形式。
其实转化成任意进制都是一样的。
初学者最容易犯的错误!!!!!!!
犯错:(-617)D=(-1151)O=(-269)H
原因分析:如果是正数的话,上面的思路是正确的,但是由于正数和负数在原码、反码、补码转换上的差别,所以按照正数的求解思路去对负数进行求解是不对的。
正确的方法是:首先将-617用补码表示出来,然后再转换成八进制和十六进制(补码)即可。
注:二进制补码要用16位。
正确答案::(-617)D=(176627)O=(fd97)H
负数十进制转换成八进制或十六进制方法
如(-12)10=( )8=( )16
第一步:转换成二进制
1000 0000 0000 1100
第二步:补码,取反加一
注意:取反时符号位不变!
1111 1111 1111 0100
第三步:转换成八进制是三位一结合:177764(8)转换成十六进制是四位一结合:fff4(16)
小数
最近有些朋友提了这样的问题“0.8的十六进制是多少?”
0.8、0.6、0.2… …一些数字在进制之间的转化过程中确实存在麻烦。
就比如“0.8的十六进制”吧!
无论怎么乘以16,它的余数总也乘不尽,总是余0.8具体方法如下:
0.8*16=12.8
0.8*16=12.8
取每一个结果的整数部分为12既十六进制的C
如果题中要求精确到小数点后3位那结果就是0.CCC
如果题中要求精确到小数点后4位那结果就是0.CCCC现在OK了。