from http://blog.csdn.net/yanqingan/article/details/6125812
最大似然估计学习总结------MadTurtle
1. 作用
在已知试验结果(即是样本)的情况下,用来估计满足这些样本分布的参数,把可能性最大的那个参数![]() 作为真实
作为真实![]() 的参数估计。
的参数估计。
2. 离散型
设![]() 为离散型随机变量,
为离散型随机变量,![]() 为多维参数向量,如果随机变量
为多维参数向量,如果随机变量![]() 相互独立且概率计算式为P{
相互独立且概率计算式为P{![]() ,则可得概率函数为P{
,则可得概率函数为P{![]() }=
}=![]() ,在
,在![]() 固定时,上式表示
固定时,上式表示![]() 的概率;当
的概率;当![]() 已知的时候,它又变成
已知的时候,它又变成![]() 的函数,可以把它记为
的函数,可以把它记为![]() ,称此函数为似然函数。似然函数值的大小意味着该样本值出现的可能性的大小,既然已经得到了样本值
,称此函数为似然函数。似然函数值的大小意味着该样本值出现的可能性的大小,既然已经得到了样本值![]() ,那么它出现的可能性应该是较大的,即似然函数的值也应该是比较大的,因而最大似然估计就是选择使
,那么它出现的可能性应该是较大的,即似然函数的值也应该是比较大的,因而最大似然估计就是选择使![]() 达到最大值的那个
达到最大值的那个![]() 作为真实
作为真实![]() 的估计。
的估计。
3. 连续型
设![]() 为连续型随机变量,其概率密度函数为
为连续型随机变量,其概率密度函数为![]() ,
,![]() 为从该总体中抽出的样本,同样的如果
为从该总体中抽出的样本,同样的如果![]() 相互独立且同分布,于是样本的联合概率密度为
相互独立且同分布,于是样本的联合概率密度为![]() 。大致过程同离散型一样。
。大致过程同离散型一样。
4. 关于概率密度(PDF)
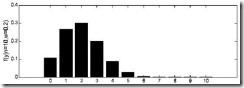
我们来考虑个简单的情况(m=k=1),即是参数和样本都为1的情况。假设进行一个实验,实验次数定为10次,每次实验成功率为0.2,那么不成功的概率为0.8,用y来表示成功的次数。由于前后的实验是相互独立的,所以可以计算得到成功的次数的概率密度为:
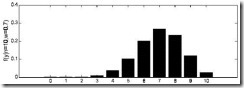
由于y的取值范围已定,而且![]() 也为已知,所以图1显示了y取不同值时的概率分布情况,而图2显示了当
也为已知,所以图1显示了y取不同值时的概率分布情况,而图2显示了当![]() 时的y值概率情况。
时的y值概率情况。
那么![]() 在[0,1]之间变化而形成的概率密度函数的集合就形成了一个模型。
在[0,1]之间变化而形成的概率密度函数的集合就形成了一个模型。
5. 最大似然估计的求法
由上面的介绍可以知道,对于图1这种情况y=2是最有可能发生的事件。但是在现实中我们还会面临另外一种情况:我们已经知道了一系列的观察值和一个感兴趣的模型,现在需要找出是哪个PDF(具体来说参数![]() 为多少时)产生出来的这些观察值。要解决这个问题,就需要用到参数估计的方法,在最大似然估计法中,我们对调PDF中数据向量和参数向量的角色,于是可以得到似然函数的定义为:
为多少时)产生出来的这些观察值。要解决这个问题,就需要用到参数估计的方法,在最大似然估计法中,我们对调PDF中数据向量和参数向量的角色,于是可以得到似然函数的定义为:
该函数可以理解为,在给定了样本值的情况下,关于参数向量![]() 取值情况的函数。还是以上面的简单实验情况为例,若此时给定y为7,那么可以得到关于
取值情况的函数。还是以上面的简单实验情况为例,若此时给定y为7,那么可以得到关于![]() 的似然函数为:
的似然函数为:
继续回顾前面所讲,图1,2是在给定![]() 的情况下,样本向量y取值概率的分布情况;而图3是图1,2横纵坐标轴相交换而成,它所描述的似然函数图则指出在给定样本向量y的情况下,符合该取值样本分布的各种参数向量
的情况下,样本向量y取值概率的分布情况;而图3是图1,2横纵坐标轴相交换而成,它所描述的似然函数图则指出在给定样本向量y的情况下,符合该取值样本分布的各种参数向量![]() 的可能性。若
的可能性。若![]() 相比于
相比于![]() ,使得y=7出现的可能性要高,那么理所当然的
,使得y=7出现的可能性要高,那么理所当然的![]() 要比
要比![]() 更加接近于真正的估计参数。所以求
更加接近于真正的估计参数。所以求![]() 的极大似然估计就归结为求似然函数
的极大似然估计就归结为求似然函数![]() 的最大值点。那么
的最大值点。那么![]() 取何值时似然函数
取何值时似然函数![]() 最大,这就需要用到高等数学中求导的概念,如果是多维参数向量那么就是求偏导。
最大,这就需要用到高等数学中求导的概念,如果是多维参数向量那么就是求偏导。
主要注意的是多数情况下,直接对变量进行求导反而会使得计算式子更加的复杂,此时可以借用对数函数。由于对数函数是单调增函数,所以![]() 与
与![]() 具有相同的最大值点,而在许多情况下,求
具有相同的最大值点,而在许多情况下,求![]() 的最大值点比较简单。于是,我们将求
的最大值点比较简单。于是,我们将求![]() 的最大值点改为求
的最大值点改为求![]() 的最大值点。
的最大值点。
若该似然函数的导数存在,那么对![]() 关于参数向量的各个参数求导数(当前情况向量维数为1),并命其等于零,得到方程组:
关于参数向量的各个参数求导数(当前情况向量维数为1),并命其等于零,得到方程组:
可以求得![]() 时似然函数有极值,为了进一步判断该点位最大值而不是最小值,可以继续求二阶导来判断函数的凹凸性,如果
时似然函数有极值,为了进一步判断该点位最大值而不是最小值,可以继续求二阶导来判断函数的凹凸性,如果![]() 的二阶导为负数那么即是最大值,这里再不细说。
的二阶导为负数那么即是最大值,这里再不细说。
还要指出,若函数![]() 关于
关于![]() 的导数不存在,我们就无法得到似然方程组,这时就必须用其它的方法来求最大似然估计值,例如用有界函数的增减性去求
的导数不存在,我们就无法得到似然方程组,这时就必须用其它的方法来求最大似然估计值,例如用有界函数的增减性去求![]() 的最大值点
的最大值点
6. 总结
最大似然估计,只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
求最大似然函数估计值的一般步骤:
(1) 写出似然函数
(2) 对似然函数取对数,并整理
(3) 求导数
(4) 解似然方程
对于最大似然估计方法的应用,需要结合特定的环境,因为它需要你提供样本的已知模型进而来估算参数,例如在模式识别中,我们可以规定目标符合高斯模型。而且对于该算法,我理解为,“知道”和“能用”就行,没必要在程序设计时将该部分实现,因为在大多数程序中只会用到我最后推导出来的结果。个人建议,如有问题望有经验者指出。在文献[1]中讲解了本文的相关理论内容,在文献[2]附有3个推导例子。
7. 参考文献
[1]I.J. Myung. Tutorial on maximum likelihood estimation[J]. Journal of Mathematical Psychology, 2003, 90-100.
[2] http://edu6.teacher.com.cn/ttg006a/chap7/jiangjie/72.htm