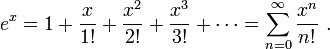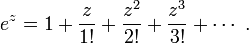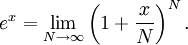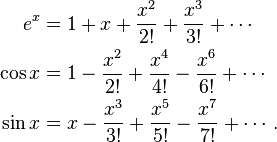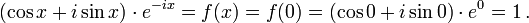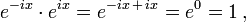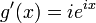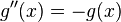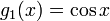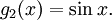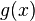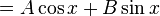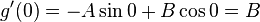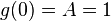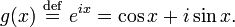Formal development of Complex Number

Formal development of Complex Number

http://en.wikipedia.org/wiki/Complex_number#Formal_development

In a rigorous setting, it is not acceptable to simply assume that there exists a number whose square is -1. The definition must therefore be a little less intuitive, building on the knowledge of real numbers. Write C for R², the set of ordered pairs of real numbers, and define operations on complex numbers in C according to

(a, b) + (c, d) = (a + c, b + d)
(a, b)·(c, d) = (a·c − b·d, b·c + a·d)

Since (0, 1)·(0, 1) = (−1, 0), we have found i by constructing it, not postulating it. We can associate the numbers (a, 0) with the real numbers, and write i = (0, 1). It is then just a matter of notation to express (a, b) as a + ib.

--------------

http://en.wikipedia.org/wiki/Euler%27s_formula

Definitions of complex exponentiation

Main articles: Exponentiation and Exponential function

In general, raising e to a positive integer exponent has a simple interpretation in terms of repeated multiplication of e. Raising e to zero or a negative integer exponent can be understood as repeated division. A rational number exponent can be defined by radicals of e, and an irrational number exponent can be defined by finding rational-number exponents that are arbitrarily close to the irrational-number exponent, in a limit process. However, to define and understand a complex number exponent of e, a different type of generalization is required for the concept of exponentiation.

In fact, several definitions are possible. All of them can be proven to be well-defined and equivalent, although the proofs are not included in this article.

Taylor series definition

It is well-known that, for any real x, the following series is equal to e^x:

$e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{n=0}^\infty\frac{x^n}{n!}~.$

(in other words, this is the Taylor series for the real exponential function, and it has an infinite radius of convergence). This invites the following definition of e^z for complex z:

$e^z = 1 + \frac{z}{1!} + \frac{z^2}{2!} + \frac{z^3}{3!} + \cdots ~.$

This can be proven to be well-defined; in particular, the series converges for any z.

Analytic continuation definition

A simple-to-state, equivalent definition is that e^z, for complex z, is the analytic continuation of the function e^x for real x. This can be proven to be well-defined; in particular, it yields a single-valued function on the complex plane.

Limit definition

It is well-known that, for any real x, the following limit is equal to e^x:

$e^x = \lim_{N \rightarrow \infty} \left(1+\frac{x}{N}\right)^N.$

This motivates the following definition of e^z for complex z:

$e^z = \lim_{N \rightarrow \infty} \left(1+\frac{z}{N}\right)^N.$

Differential equation definition

For real x, the function f(x)=e^x is well-known to be the unique real function satisfying the differential equation:

$f'(x)=f(x),\;\;\; f(0)=1$

for all x. This motivates a definition of f(z)=e^z for complex z as the function that satisfies the differential equation:

$f'(z)=f(z),\;\;\; f(0)=1$

for all complex z, where the derivative in f'(z) is defined in the sense of a complex derivative. This can be proven to yield a unique function which is well-defined everywhere on the complex plane.

Proofs

Various proofs of this formula are possible. The first proof below starts with the "Taylor series definition" of e^z, while the other two use the "Differential equation definition" of e^z (see above).

Using Taylor series

Here is a proof of Euler's formula using Taylor series expansions as well as basic facts about the powers of i:

$\text{[math]}$

and so on. The functions e^x, cos x and sin x of the (real) variable x can be expressed using their Taylor expansions around zero:

$\text{[math]}$

For complex z we define each of these functions by the above series, replacing the real variable x with the complex variable z. This is possible because the radius of convergence of each series is infinite. We then find that

$\text{[math]}$

The rearrangement of terms is justified because each series is absolutely convergent. Taking z = x to be a real number gives the original identity as Euler discovered it.

Q.E.D.

Using calculus

Define the (possibly complex) function ƒ(x), of real variable x, as

$f(x) = (\cos x + i\sin x)\cdot e^{-ix}. \$

The derivative of ƒ(x), according to the product rule, is:

$\text{[math]}$

Therefore, ƒ(x) must be a constant function in x. Because ƒ(0) is known, the constant that ƒ(x) equals for all real x is also known. Thus,

$(\cos x + i\sin x)\cdot e^{-ix} = f(x) = f(0) = (\cos 0 + i\sin 0)\cdot e^0 = 1 \,.$

Multiplying both sides by e^ix and using

$e^{-ix} \cdot e^{ix} = e^{-ix \, + \, ix} = e^0 = 1 \,,$

it follows that

$e^{ix} = \cos x + i \sin x \ .$

Q.E.D.

Using ordinary differential equations

Define the function g(x) by

$g(x) \ \stackrel{\mathrm{def}}{=}\ e^{ix} .\$

Considering that i is constant, the first and second derivatives of g(x) are

$g'(x) = i e^{ix} \$
$g''(x) = i^2 e^{ix} = -e^{ix} \$

because i ² = −1 by definition. From this the following 2^nd-order linear ordinary differential equation is constructed:

$g''(x) = -g(x) \$

or

$g''(x) + g(x) = 0. \$

Being a 2^nd-order differential equation, there are two linearly independent solutions that satisfy it:

$g_1(x) = \cos x \$
$g_2(x) = \sin x. \$

Both cos and sin are real functions in which the 2^nd derivative is identical to the negative of that function. Any linear combination of solutions to a homogeneous differential equation is also a solution. Then, in general, the solution to the differential equation is

$g(x)\,$ $= A g_1(x) + B g_2(x) \$

$= A \cos x + B \sin x \$

for any constants A and B. But not all values of these two constants satisfy the known initial conditions for g(x):

$g(0) = e^{i0} = 1 \$
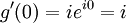$g'(0) = i e^{i0} = i \$ .

However these same initial conditions (applied to the general solution) are

$g(0) = A \cos 0 + B \sin 0 = A \$
$g'(0) = -A \sin 0 + B \cos 0 = B \$

resulting in

$g(0) = A = 1 \$
$g'(0) = B = i \$

and, finally,

$g(x) \ \stackrel{\mathrm{def}}{=}\ e^{ix} = \cos x + i \sin x. \$
相关阅读:
allure2生成html报告
 H5如何测试？
请描述什么是性能测试、什么是负载测试、什么是压力测试？
Web／App端自动化测试对比
 如果给你一台电梯，请问你如何测试它
 PC、APP、H5三端测试的相同与不同
 App测试工具选择
 app测试和web测试的区别
 unittest单元测试框架详解
 Jmeter之逻辑控制器(Logic Controller)
原文地址：https://www.cnblogs.com/smwikipedia/p/1444062.html

$g(x)\,$	$= A g_1(x) + B g_2(x) \$
	$= A \cos x + B \sin x \$

Formal development of Complex Number

Taylor series definition

Analytic continuation definition

Limit definition

Differential equation definition

Proofs

Using Taylor series

Using calculus

Using ordinary differential equations