原文链接：https://arxiv.org/abs/1902.09689
发表在：ICLR 2019
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
考虑下面的ODE,
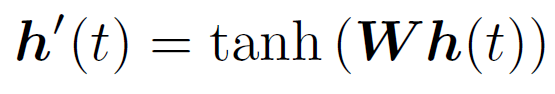
将其离散化，假设步长为
，我们有
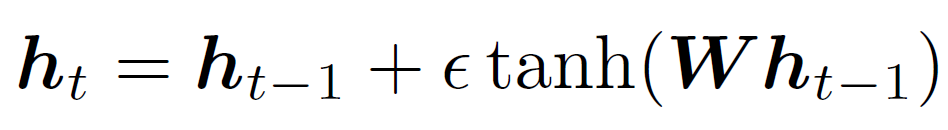
命题1：
如果f的Jacobian矩阵的最大特征值实部小于0，那么ODE的解时稳定的.
我们希望的是，不仅要稳定，而且还希望系统不要稳定的收敛速度太快。理想的情况就是，
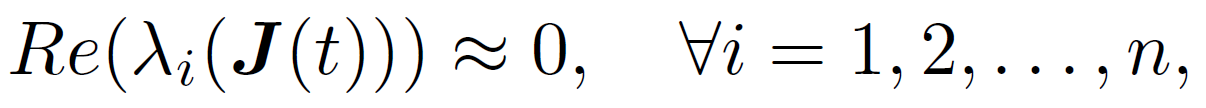
这可以认为是系统的临界状态，稳态和非稳态的切换的点。
对上面的第一个式子两边对初值h(0)做微分，我们有
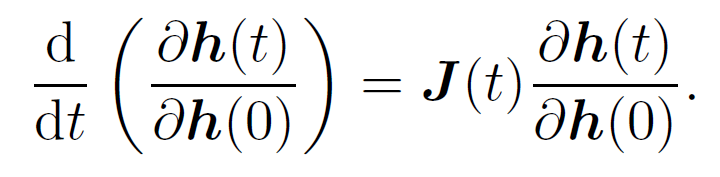
令
，我们有，
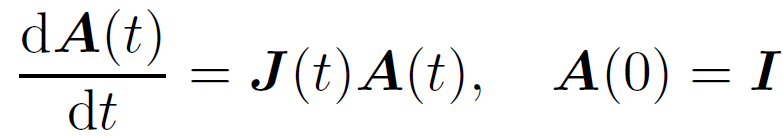
如果临界状态满足，那么A(t)就近似保持长值。
前方重点。。。
这里引出反对称矩阵，M, i.e.,
需要指出的是，反对称矩阵的特征值的实部为0，
考虑下面的ODE，
反对称，并且Jocobian矩阵为，
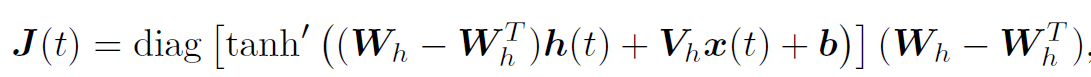
并且可以证明它的特征值实部为0.
离散化后，得到，
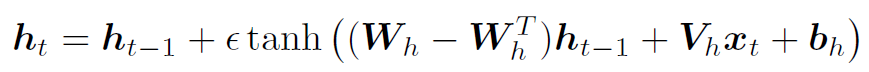
PS：只有n(n-1)/2的自由度，参数少了一半。
我们需要注意的是，离散化之后的，特征值的模长并非是小于1的，i.e., 不满足
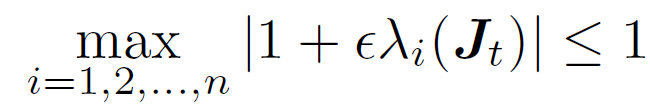
所以我们在tanh里面加一个平移项，
核心就到这里了，其它的就是变形，和simulations了。